College Algebra Essentials, Books a la Carte Edition Plus Mymathlab with New Pearson Etext -- Access Card Package
College Algebra Essentials, Books a la Carte Edition Plus Mymathlab with New Pearson Etext -- Access Card Package
4th Edition
ISBN: 9780321869715
Author: Robert F. Blitzer
Publisher: PEARSON
bartleby

Concept explainers

Inverse Normal Distribution
The method used for finding the corresponding z-critical value in a normal distribution using the known probability is said to be an inverse normal distribution. The inverse normal distribution is a continuous probability distribution with a family of tw…
Mean, Median, Mode
It is a descriptive summary of a data set. It can be defined by using some of the measures. The central tendencies do not provide information regarding individual data from the dataset. However, they give a summary of the data set. The central tendency o…
Z-Scores
A z-score is a unit of measurement used in statistics to describe the position of a raw score in terms of its distance from the mean, measured with reference to standard deviation from the mean. Z-scores are useful in statistics because they allow compar…
bartleby

Videos

Textbook Question
Book Icon
Chapter 4.4, Problem 152E

U.S. soldiers fight Russian troops who have invaded New York City. Incoming missiles from Russian submarines and warships ravage the Manhattan skyline. It’s just another scenario for the multi-billion-dollar video games Call of Duty, which have sold more than 100 million games since the franchise’s birth in 2003.

Chapter 4.4, Problem 152E, U.S. soldiers fight Russian troops who have invaded New York City. Incoming missiles from Russian , example 1

The table shows the annual retail sales for Call of Duty video games from 2004 through 2010. Create a scatter plot for the data. Based on the shape of the scatter plot, would a logarithmic function, an exponential function, or a linear function be the best choice for modeling the data?

Annual Retail Sales for Call of Duty Games

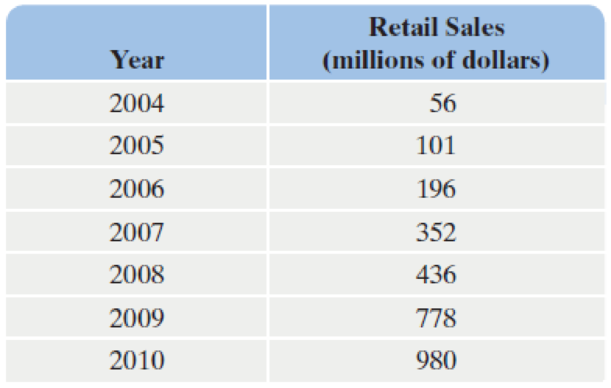
Chapter 4.4, Problem 152E, U.S. soldiers fight Russian troops who have invaded New York City. Incoming missiles from Russian , example 2

Source: The NPD Group

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 4.4, Problem 151E
Next
Chapter 4.5, Problem 1CP
Students have asked these similar questions
Practice k Help ises A 96 Anewer The probability that you get a sum of at least 10 is Determine the number of ways that the specified event can occur when two number cubes are rolled. 1. Getting a sum of 9 or 10 3. Getting a sum less than 5 2. Getting a sum of 6 or 7 4. Getting a sum that is odd Tell whether you would use the addition principle or the multiplication principle to determine the total number of possible outcomes for the situation described. 5. Rolling three number cubes 6. Getting a sum of 10 or 12 after rolling three number cubes A set of playing cards contains four groups of cards designated by color (black, red, yellow, and green) with cards numbered from 1 to 14 in each group. Determine the number of ways that the specified event can occur when a card is drawn from the set. 7. Drawing a 13 or 14 9. Drawing a number less than 4 8. Drawing a yellow or green card 10. Drawing a black, red, or green car The spinner is divided into equal parts. Find the specified…
Answer the questions
How can I prepare for me Unit 3 test in algebra 1? I am in 9th grade.

Chapter 4 Solutions

College Algebra Essentials, Books a la Carte Edition Plus Mymathlab with New Pearson Etext -- Access Card Package

Ch. 4.1 - Use the exponential function in Example l to find...Ch. 4.1 - Prob. 2CPCh. 4.1 - Prob. 3CPCh. 4.1 - Prob. 4CPCh. 4.1 - Prob. 5CPCh. 4.1 - Prob. 6CPCh. 4.1 - A sum of 10,000 is invested at an annual rate of...Ch. 4.1 - Prob. 1CVCCh. 4.1 - Prob. 2CVCCh. 4.1 - Fill in each blank so that the resulting statement...
Ch. 4.1 - Fill in each blank so that the resulting statement...Ch. 4.1 - Prob. 5CVCCh. 4.1 - Prob. 1ECh. 4.1 - Prob. 2ECh. 4.1 - Prob. 3ECh. 4.1 - Prob. 4ECh. 4.1 - Prob. 5ECh. 4.1 - In Exercises 110, approximate each number using a...Ch. 4.1 - Prob. 7ECh. 4.1 - Prob. 8ECh. 4.1 - Prob. 9ECh. 4.1 - Prob. 10ECh. 4.1 - Prob. 11ECh. 4.1 - In Exercises 1118, graph each function by making a...Ch. 4.1 - Prob. 13ECh. 4.1 - Prob. 14ECh. 4.1 - Prob. 15ECh. 4.1 - Prob. 16ECh. 4.1 - Prob. 17ECh. 4.1 - Prob. 18ECh. 4.1 - Prob. 19ECh. 4.1 - Prob. 20ECh. 4.1 - Prob. 21ECh. 4.1 - Prob. 22ECh. 4.1 - Prob. 23ECh. 4.1 - Prob. 24ECh. 4.1 - Prob. 25ECh. 4.1 - In Exercises 2534, begin by graphing f(x)=2x. Then...Ch. 4.1 - Prob. 27ECh. 4.1 - Prob. 28ECh. 4.1 - Prob. 29ECh. 4.1 - Prob. 30ECh. 4.1 - Prob. 31ECh. 4.1 - Prob. 32ECh. 4.1 - Prob. 33ECh. 4.1 - Prob. 34ECh. 4.1 - The figure shows the graph of f(x)=ex. In...Ch. 4.1 - The figure shows the graph of f(x)=ex. In...Ch. 4.1 - Prob. 37ECh. 4.1 - Prob. 38ECh. 4.1 - The figure shows the graph of f(x)=ex. In...Ch. 4.1 - Prob. 40ECh. 4.1 - Prob. 41ECh. 4.1 - Prob. 42ECh. 4.1 - Prob. 43ECh. 4.1 - Prob. 44ECh. 4.1 - The figure shows the graph of f(x)=ex. In...Ch. 4.1 - Prob. 46ECh. 4.1 - Prob. 47ECh. 4.1 - Prob. 48ECh. 4.1 - Prob. 49ECh. 4.1 - Prob. 50ECh. 4.1 - Prob. 51ECh. 4.1 - Prob. 52ECh. 4.1 - Use the compound interest formulas A=P(1+rn)nt and...Ch. 4.1 - Use the compound interest formulas A=P(1+rn)nt and...Ch. 4.1 - Prob. 55ECh. 4.1 - Prob. 56ECh. 4.1 - Prob. 57ECh. 4.1 - Prob. 58ECh. 4.1 - Prob. 59ECh. 4.1 - Prob. 60ECh. 4.1 - Prob. 61ECh. 4.1 - Prob. 62ECh. 4.1 - Prob. 63ECh. 4.1 - Prob. 64ECh. 4.1 - Prob. 65ECh. 4.1 - Prob. 66ECh. 4.1 - Prob. 67ECh. 4.1 - The formulas S=C(1+r)t models inflation, where C =...Ch. 4.1 - Prob. 69ECh. 4.1 - A decimal approximation for is 3.141593. Use a...Ch. 4.1 - Prob. 71ECh. 4.1 - Prob. 72ECh. 4.1 - Prob. 73ECh. 4.1 - Prob. 74ECh. 4.1 - Prob. 75ECh. 4.1 - Prob. 76ECh. 4.1 - Prob. 77ECh. 4.1 - Prob. 78ECh. 4.1 - Use a calculator to evaluate (1+1x)x for x = 10,...Ch. 4.1 - Prob. 80ECh. 4.1 - Prob. 81ECh. 4.1 - Prob. 82ECh. 4.1 - Prob. 83ECh. 4.1 - Make Sense? In Exercises 83-86, determine whether...Ch. 4.1 - Make Sense? In Exercises 83–86, determine whether...Ch. 4.1 - Make Sense? In Exercises 83-86, determine whether...Ch. 4.1 - Prob. 87ECh. 4.1 - In Exercises 87-90, determine whether each...Ch. 4.1 - In Exercises 87-90, determine whether each...Ch. 4.1 - Prob. 90ECh. 4.1 - Prob. 91ECh. 4.1 - Prob. 92ECh. 4.1 - Prob. 93ECh. 4.1 - Prob. 94ECh. 4.1 - Prob. 95ECh. 4.1 - Prob. 96ECh. 4.2 - Check Point 1 Write each equation in its...Ch. 4.2 - Prob. 2CPCh. 4.2 - Prob. 3CPCh. 4.2 - Prob. 4CPCh. 4.2 - Prob. 5CPCh. 4.2 - Prob. 6CPCh. 4.2 - Prob. 7CPCh. 4.2 - Prob. 8CPCh. 4.2 - Use the formula in Example 9 to solve this...Ch. 4.2 - Prob. 10CPCh. 4.2 - Prob. 11CPCh. 4.2 - Prob. 1CVCCh. 4.2 - Prob. 2CVCCh. 4.2 - Prob. 3CVCCh. 4.2 - Prob. 4CVCCh. 4.2 - Prob. 5CVCCh. 4.2 - Prob. 6CVCCh. 4.2 - Prob. 7CVCCh. 4.2 - Prob. 8CVCCh. 4.2 - Prob. 9CVCCh. 4.2 - Prob. 10CVCCh. 4.2 - Prob. 11CVCCh. 4.2 - Prob. 12CVCCh. 4.2 - Prob. 13CVCCh. 4.2 - Prob. 14CVCCh. 4.2 - Prob. 15CVCCh. 4.2 - Prob. 1ECh. 4.2 - Prob. 2ECh. 4.2 - Prob. 3ECh. 4.2 - Prob. 4ECh. 4.2 - Prob. 5ECh. 4.2 - Prob. 6ECh. 4.2 - Prob. 7ECh. 4.2 - Prob. 8ECh. 4.2 - Prob. 9ECh. 4.2 - Prob. 10ECh. 4.2 - Prob. 11ECh. 4.2 - Prob. 12ECh. 4.2 - In Exercises 920, write each equation in its...Ch. 4.2 - Prob. 14ECh. 4.2 - Prob. 15ECh. 4.2 - Prob. 16ECh. 4.2 - Prob. 17ECh. 4.2 - Prob. 18ECh. 4.2 - Prob. 19ECh. 4.2 - Prob. 20ECh. 4.2 - Prob. 21ECh. 4.2 - Prob. 22ECh. 4.2 - Prob. 23ECh. 4.2 - Prob. 24ECh. 4.2 - Prob. 25ECh. 4.2 - Prob. 26ECh. 4.2 - Prob. 27ECh. 4.2 - In Exercises 2142, evaluate each expression...Ch. 4.2 - In Exercises 2142, evaluate each expression...Ch. 4.2 - Prob. 30ECh. 4.2 - Prob. 31ECh. 4.2 - Prob. 32ECh. 4.2 - Prob. 33ECh. 4.2 - Prob. 34ECh. 4.2 - Prob. 35ECh. 4.2 - Prob. 36ECh. 4.2 - Prob. 37ECh. 4.2 - Prob. 38ECh. 4.2 - Prob. 39ECh. 4.2 - Prob. 40ECh. 4.2 - Prob. 41ECh. 4.2 - Prob. 42ECh. 4.2 - Prob. 43ECh. 4.2 - Prob. 44ECh. 4.2 - Prob. 45ECh. 4.2 - Prob. 46ECh. 4.2 - Prob. 47ECh. 4.2 - Prob. 48ECh. 4.2 - Prob. 49ECh. 4.2 - Prob. 50ECh. 4.2 - Prob. 51ECh. 4.2 - Prob. 52ECh. 4.2 - Prob. 53ECh. 4.2 - Prob. 54ECh. 4.2 - Prob. 55ECh. 4.2 - Prob. 56ECh. 4.2 - Prob. 57ECh. 4.2 - Prob. 58ECh. 4.2 - Prob. 59ECh. 4.2 - Prob. 60ECh. 4.2 - Prob. 61ECh. 4.2 - Prob. 62ECh. 4.2 - Prob. 63ECh. 4.2 - Prob. 64ECh. 4.2 - Prob. 65ECh. 4.2 - Prob. 66ECh. 4.2 - Prob. 67ECh. 4.2 - Prob. 68ECh. 4.2 - Prob. 69ECh. 4.2 - Prob. 70ECh. 4.2 - Prob. 71ECh. 4.2 - Prob. 72ECh. 4.2 - Prob. 73ECh. 4.2 - The figure shows the graph of f(x) = ln x. In...Ch. 4.2 - Prob. 75ECh. 4.2 - Prob. 76ECh. 4.2 - Prob. 77ECh. 4.2 - Prob. 78ECh. 4.2 - Prob. 79ECh. 4.2 - Prob. 80ECh. 4.2 - Prob. 81ECh. 4.2 - In Exercises 81100, evaluate or simplify each...Ch. 4.2 - Prob. 83ECh. 4.2 - Prob. 84ECh. 4.2 - In Exercises 81100, evaluate or simplify each...Ch. 4.2 - In Exercises 81100, evaluate or simplify each...Ch. 4.2 - Prob. 87ECh. 4.2 - Prob. 88ECh. 4.2 - Prob. 89ECh. 4.2 - In Exercises 81100, evaluate or simplify each...Ch. 4.2 - Prob. 91ECh. 4.2 - Prob. 92ECh. 4.2 - Prob. 93ECh. 4.2 - Prob. 94ECh. 4.2 - Prob. 95ECh. 4.2 - Prob. 96ECh. 4.2 - Prob. 97ECh. 4.2 - Prob. 98ECh. 4.2 - Prob. 99ECh. 4.2 - Prob. 100ECh. 4.2 - Prob. 101ECh. 4.2 - Prob. 102ECh. 4.2 - Prob. 103ECh. 4.2 - Prob. 104ECh. 4.2 - Prob. 105ECh. 4.2 - Prob. 106ECh. 4.2 - Prob. 107ECh. 4.2 - Prob. 108ECh. 4.2 - Prob. 109ECh. 4.2 - Prob. 110ECh. 4.2 - Prob. 111ECh. 4.2 - Prob. 112ECh. 4.2 - Prob. 113ECh. 4.2 - Prob. 114ECh. 4.2 - The bar graph indicates that the percentage of...Ch. 4.2 - Prob. 116ECh. 4.2 - Prob. 117ECh. 4.2 - Prob. 118ECh. 4.2 - Students in a psychology class took a final...Ch. 4.2 - Describe the relationship between an equation in...Ch. 4.2 - Prob. 121ECh. 4.2 - Prob. 122ECh. 4.2 - Describe the following property using words: logb...Ch. 4.2 - Prob. 124ECh. 4.2 - Prob. 125ECh. 4.2 - Prob. 126ECh. 4.2 - Prob. 127ECh. 4.2 - Prob. 128ECh. 4.2 - Prob. 129ECh. 4.2 - Prob. 130ECh. 4.2 - Prob. 131ECh. 4.2 - Prob. 132ECh. 4.2 - Prob. 133ECh. 4.2 - Prob. 134ECh. 4.2 - Prob. 135ECh. 4.2 - Make Sense? In Exercises 135138, determine whether...Ch. 4.2 - Prob. 137ECh. 4.2 - Prob. 138ECh. 4.2 - Prob. 139ECh. 4.2 - Prob. 140ECh. 4.2 - Prob. 141ECh. 4.2 - Prob. 142ECh. 4.2 - Prob. 143ECh. 4.2 - Without using a calculator, find the exact value...Ch. 4.2 - Prob. 145ECh. 4.2 - Prob. 146ECh. 4.2 - Prob. 147ECh. 4.2 - Exercises 150152 will help you prepare for the...Ch. 4.2 - Exercises 150152 will help you prepare for the...Ch. 4.3 - Prob. 1CPCh. 4.3 - Prob. 2CPCh. 4.3 - Prob. 3CPCh. 4.3 - Prob. 4CPCh. 4.3 - Prob. 5CPCh. 4.3 - Prob. 6CPCh. 4.3 - Prob. 7CPCh. 4.3 - Prob. 8CPCh. 4.3 - Prob. 1CVCCh. 4.3 - Prob. 2CVCCh. 4.3 - The power rule for logarithms states that logb M p...Ch. 4.3 - Prob. 4CVCCh. 4.3 - Prob. 1ECh. 4.3 - Prob. 2ECh. 4.3 - Prob. 3ECh. 4.3 - Prob. 4ECh. 4.3 - Prob. 5ECh. 4.3 - Prob. 6ECh. 4.3 - Prob. 7ECh. 4.3 - Prob. 8ECh. 4.3 - Prob. 9ECh. 4.3 - Prob. 10ECh. 4.3 - Prob. 11ECh. 4.3 - Prob. 12ECh. 4.3 - Prob. 13ECh. 4.3 - Prob. 14ECh. 4.3 - Prob. 15ECh. 4.3 - Prob. 16ECh. 4.3 - Prob. 17ECh. 4.3 - In Exercises 140, use properties of logarithms to...Ch. 4.3 - Prob. 19ECh. 4.3 - Prob. 20ECh. 4.3 - Prob. 21ECh. 4.3 - Prob. 22ECh. 4.3 - Prob. 23ECh. 4.3 - Prob. 24ECh. 4.3 - Prob. 25ECh. 4.3 - Prob. 26ECh. 4.3 - Prob. 27ECh. 4.3 - Prob. 28ECh. 4.3 - Prob. 29ECh. 4.3 - Prob. 30ECh. 4.3 - Prob. 31ECh. 4.3 - Prob. 32ECh. 4.3 - Prob. 33ECh. 4.3 - Prob. 34ECh. 4.3 - Prob. 35ECh. 4.3 - Prob. 36ECh. 4.3 - Prob. 37ECh. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - Prob. 40ECh. 4.3 - Prob. 41ECh. 4.3 - Prob. 42ECh. 4.3 - Prob. 43ECh. 4.3 - Prob. 44ECh. 4.3 - Prob. 45ECh. 4.3 - Prob. 46ECh. 4.3 - Prob. 47ECh. 4.3 - Prob. 48ECh. 4.3 - Prob. 49ECh. 4.3 - Prob. 50ECh. 4.3 - Prob. 51ECh. 4.3 - Prob. 52ECh. 4.3 - Prob. 53ECh. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Prob. 57ECh. 4.3 - Prob. 58ECh. 4.3 - Prob. 59ECh. 4.3 - Prob. 60ECh. 4.3 - In Exercises 4170, use properties of logarithms to...Ch. 4.3 - Prob. 62ECh. 4.3 - Prob. 63ECh. 4.3 - Prob. 64ECh. 4.3 - Prob. 65ECh. 4.3 - Prob. 66ECh. 4.3 - Prob. 67ECh. 4.3 - Prob. 68ECh. 4.3 - Prob. 69ECh. 4.3 - Prob. 70ECh. 4.3 - Prob. 71ECh. 4.3 - Prob. 72ECh. 4.3 - Prob. 73ECh. 4.3 - Prob. 74ECh. 4.3 - Prob. 75ECh. 4.3 - Prob. 76ECh. 4.3 - In Exercises 71-78, use common logarithms or...Ch. 4.3 - In Exercises 71-78, use common logarithms or...Ch. 4.3 - Prob. 79ECh. 4.3 - In Exercises 79-82, use a graphing utility and the...Ch. 4.3 - Prob. 81ECh. 4.3 - Prob. 82ECh. 4.3 - Prob. 83ECh. 4.3 - Prob. 84ECh. 4.3 - Prob. 85ECh. 4.3 - Prob. 86ECh. 4.3 - Prob. 87ECh. 4.3 - Prob. 88ECh. 4.3 - Prob. 89ECh. 4.3 - Prob. 90ECh. 4.3 - Prob. 91ECh. 4.3 - Prob. 92ECh. 4.3 - Prob. 93ECh. 4.3 - Prob. 94ECh. 4.3 - Prob. 95ECh. 4.3 - Prob. 96ECh. 4.3 - Prob. 97ECh. 4.3 - Prob. 98ECh. 4.3 - Prob. 99ECh. 4.3 - Prob. 100ECh. 4.3 - Prob. 101ECh. 4.3 - Prob. 102ECh. 4.3 - Prob. 103ECh. 4.3 - Prob. 104ECh. 4.3 - Prob. 105ECh. 4.3 - Prob. 106ECh. 4.3 - Prob. 107ECh. 4.3 - Prob. 108ECh. 4.3 - Prob. 109ECh. 4.3 - Prob. 110ECh. 4.3 - You overhear a student talking about a property of...Ch. 4.3 - Prob. 112ECh. 4.3 - Prob. 113ECh. 4.3 - Prob. 114ECh. 4.3 - Prob. 115ECh. 4.3 - Prob. 116ECh. 4.3 - Prob. 117ECh. 4.3 - Disprove each statement in Exercises 116120 by...Ch. 4.3 - Prob. 119ECh. 4.3 - Prob. 120ECh. 4.3 - Prob. 121ECh. 4.3 - Make Sense? In Exercises 121124, determine whether...Ch. 4.3 - Prob. 123ECh. 4.3 - Prob. 124ECh. 4.3 - Prob. 125ECh. 4.3 - Prob. 126ECh. 4.3 - In Exercises 125128, determine whether each...Ch. 4.3 - Prob. 128ECh. 4.3 - Prob. 129ECh. 4.3 - Prob. 130ECh. 4.3 - Prob. 131ECh. 4.3 - Prob. 132ECh. 4.3 - Prob. 133ECh. 4.3 - Prob. 134ECh. 4.3 - Prob. 135ECh. 4.3 - Prob. 136ECh. 4.4 - Solve: a. 53x6 = 125 b. 8x+2 = 4x3.Ch. 4.4 - Solve: a. 5x = 134 b. 10x = 8000.Ch. 4.4 - Solve: 7e2x 5 = 58. Find the solution set and...Ch. 4.4 - Prob. 4CPCh. 4.4 - Solve: e2x 8ex + 7 = 0. Find the solution set and...Ch. 4.4 - Prob. 6CPCh. 4.4 - Prob. 7CPCh. 4.4 - Prob. 8CPCh. 4.4 - Use the formula in Example 9 to answer this...Ch. 4.4 - How long, to the nearest tenth of a year, will it...Ch. 4.4 - Prob. 11CPCh. 4.4 - Fill in each blank so that the resulting statement...Ch. 4.4 - Prob. 2CVCCh. 4.4 - Prob. 3CVCCh. 4.4 - Fill in each blank so that the resulting statement...Ch. 4.4 - Prob. 5CVCCh. 4.4 - Prob. 6CVCCh. 4.4 - Prob. 7CVCCh. 4.4 - Prob. 8CVCCh. 4.4 - Fill in each blank so that the resulting statement...Ch. 4.4 - Fill in each blank so that the resulting statement...Ch. 4.4 - Prob. 11CVCCh. 4.4 - Prob. 1ECh. 4.4 - Prob. 2ECh. 4.4 - Prob. 3ECh. 4.4 - Prob. 4ECh. 4.4 - Prob. 5ECh. 4.4 - Prob. 6ECh. 4.4 - Prob. 7ECh. 4.4 - Prob. 8ECh. 4.4 - Prob. 9ECh. 4.4 - Prob. 10ECh. 4.4 - Prob. 11ECh. 4.4 - Prob. 12ECh. 4.4 - Prob. 13ECh. 4.4 - Prob. 14ECh. 4.4 - Prob. 15ECh. 4.4 - Prob. 16ECh. 4.4 - Prob. 17ECh. 4.4 - Prob. 18ECh. 4.4 - Prob. 19ECh. 4.4 - Prob. 20ECh. 4.4 - Prob. 21ECh. 4.4 - Prob. 22ECh. 4.4 - Prob. 23ECh. 4.4 - Prob. 24ECh. 4.4 - Prob. 25ECh. 4.4 - Prob. 26ECh. 4.4 - Prob. 27ECh. 4.4 - Prob. 28ECh. 4.4 - Prob. 29ECh. 4.4 - Prob. 30ECh. 4.4 - Prob. 31ECh. 4.4 - Prob. 32ECh. 4.4 - Prob. 33ECh. 4.4 - Prob. 34ECh. 4.4 - Prob. 35ECh. 4.4 - Prob. 36ECh. 4.4 - Prob. 37ECh. 4.4 - Prob. 38ECh. 4.4 - Solve each exponential equation in Exercises 2348....Ch. 4.4 - Prob. 40ECh. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Prob. 43ECh. 4.4 - Prob. 44ECh. 4.4 - Prob. 45ECh. 4.4 - Prob. 46ECh. 4.4 - Prob. 47ECh. 4.4 - Prob. 48ECh. 4.4 - Prob. 49ECh. 4.4 - Prob. 50ECh. 4.4 - Prob. 51ECh. 4.4 - Prob. 52ECh. 4.4 - Prob. 53ECh. 4.4 - Prob. 54ECh. 4.4 - Prob. 55ECh. 4.4 - Prob. 56ECh. 4.4 - Prob. 57ECh. 4.4 - Prob. 58ECh. 4.4 - Prob. 59ECh. 4.4 - Prob. 60ECh. 4.4 - Prob. 61ECh. 4.4 - Prob. 62ECh. 4.4 - Prob. 63ECh. 4.4 - Prob. 64ECh. 4.4 - Prob. 65ECh. 4.4 - Prob. 66ECh. 4.4 - Prob. 67ECh. 4.4 - Prob. 68ECh. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Prob. 70ECh. 4.4 - Prob. 71ECh. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Prob. 76ECh. 4.4 - Prob. 77ECh. 4.4 - Prob. 78ECh. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Prob. 80ECh. 4.4 - Prob. 81ECh. 4.4 - Prob. 82ECh. 4.4 - Prob. 83ECh. 4.4 - Prob. 84ECh. 4.4 - Prob. 85ECh. 4.4 - Prob. 86ECh. 4.4 - Prob. 87ECh. 4.4 - Prob. 88ECh. 4.4 - Prob. 89ECh. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Prob. 91ECh. 4.4 - Prob. 92ECh. 4.4 - Prob. 93ECh. 4.4 - Prob. 94ECh. 4.4 - Prob. 95ECh. 4.4 - Prob. 96ECh. 4.4 - Prob. 97ECh. 4.4 - Prob. 98ECh. 4.4 - Prob. 99ECh. 4.4 - In Exercises 93102, solve each equation....Ch. 4.4 - In Exercises 93102, solve each equation....Ch. 4.4 - In Exercises 93102, solve each equation....Ch. 4.4 - Prob. 103ECh. 4.4 - The formula A=25.1e0.0187t models the population...Ch. 4.4 - Prob. 105ECh. 4.4 - Prob. 106ECh. 4.4 - Prob. 107ECh. 4.4 - Prob. 108ECh. 4.4 - Prob. 109ECh. 4.4 - Prob. 110ECh. 4.4 - Prob. 111ECh. 4.4 - Prob. 112ECh. 4.4 - In Exercises 111-114, complete the table for a...Ch. 4.4 - Prob. 114ECh. 4.4 - Prob. 115ECh. 4.4 - Prob. 116ECh. 4.4 - Prob. 117ECh. 4.4 - Prob. 118ECh. 4.4 - Prob. 119ECh. 4.4 - Prob. 120ECh. 4.4 - Prob. 121ECh. 4.4 - Prob. 122ECh. 4.4 - Prob. 123ECh. 4.4 - Prob. 124ECh. 4.4 - Prob. 125ECh. 4.4 - In Exercises 125-132, use your graphing utility to...Ch. 4.4 - Prob. 127ECh. 4.4 - Prob. 128ECh. 4.4 - Prob. 129ECh. 4.4 - Prob. 130ECh. 4.4 - In Exercises 125-132, use your graphing utility to...Ch. 4.4 - Prob. 132ECh. 4.4 - Prob. 133ECh. 4.4 - Prob. 137ECh. 4.4 - Prob. 138ECh. 4.4 - Prob. 139ECh. 4.4 - Make Sense? In Exercises 137140, determine whether...Ch. 4.4 - Prob. 141ECh. 4.4 - Prob. 142ECh. 4.4 - Prob. 143ECh. 4.4 - Prob. 144ECh. 4.4 - Prob. 145ECh. 4.4 - Prob. 146ECh. 4.4 - Prob. 147ECh. 4.4 - Prob. 148ECh. 4.4 - Prob. 150ECh. 4.4 - Exercises 153155 will help you prepare for the...Ch. 4.4 - U.S. soldiers fight Russian troops who have...Ch. 4.5 - In 2000, the population of Africa was 807 million...Ch. 4.5 - Prob. 2CPCh. 4.5 - Prob. 3CPCh. 4.5 - Table 4.7 shows the populations of various cities,...Ch. 4.5 - Prob. 5CPCh. 4.5 - Use the models f(x) = 0.074x + 2.294 and g(x) =...Ch. 4.5 - Rewrite y = 4(7.8)x in terms of base e. Express...Ch. 4.5 - Fill in each blank so that the resulting statement...Ch. 4.5 - Fill in each blank so that the resulting statement...Ch. 4.5 - Fill in each blank so that the resulting statement...Ch. 4.5 - For each of the scatter plots in Exercises 46,...Ch. 4.5 - For each of the scatter plots in Exercises 46,...Ch. 4.5 - For each of the scatter plots in Exercises 46,...Ch. 4.5 - Fill in each blank so that the resulting statement...Ch. 4.5 - Prob. 1ECh. 4.5 - Prob. 2ECh. 4.5 - Prob. 3ECh. 4.5 - The exponential models describe the population of...Ch. 4.5 - The exponential models describe the population of...Ch. 4.5 - Prob. 6ECh. 4.5 - Prob. 7ECh. 4.5 - About the size of New Jersey, Israel has seen its...Ch. 4.5 - Prob. 9ECh. 4.5 - In Exercises 9-14, complete the table. Round...Ch. 4.5 - Prob. 11ECh. 4.5 - Prob. 12ECh. 4.5 - Prob. 13ECh. 4.5 - Prob. 14ECh. 4.5 - Prob. 15ECh. 4.5 - Prob. 16ECh. 4.5 - Prob. 17ECh. 4.5 - Prob. 18ECh. 4.5 - Prob. 19ECh. 4.5 - Prob. 20ECh. 4.5 - Prob. 21ECh. 4.5 - Prob. 22ECh. 4.5 - Prob. 23ECh. 4.5 - Prob. 24ECh. 4.5 - In Exercises 21-26, complete the table. Round...Ch. 4.5 - Prob. 26ECh. 4.5 - Prob. 27ECh. 4.5 - Use the exponential decay model, A = A0ekt, to...Ch. 4.5 - Prob. 29ECh. 4.5 - Prob. 30ECh. 4.5 - Prob. 31ECh. 4.5 - Prob. 32ECh. 4.5 - Prob. 33ECh. 4.5 - Prob. 34ECh. 4.5 - Prob. 35ECh. 4.5 - Prob. 36ECh. 4.5 - Prob. 37ECh. 4.5 - Prob. 38ECh. 4.5 - We see from the calculator screen at the bottom of...Ch. 4.5 - We see from the calculator screen at the bottom of...Ch. 4.5 - We see from the calculator screen at the bottom of...Ch. 4.5 - Prob. 42ECh. 4.5 - Prob. 43ECh. 4.5 - Prob. 44ECh. 4.5 - Prob. 45ECh. 4.5 - Prob. 46ECh. 4.5 - Prob. 47ECh. 4.5 - Exercises 4752 present data in the form of tables....Ch. 4.5 - Prob. 49ECh. 4.5 - Prob. 50ECh. 4.5 - Prob. 51ECh. 4.5 - Prob. 52ECh. 4.5 - In Exercises 5356, rewrite the equation in terms...Ch. 4.5 - Prob. 54ECh. 4.5 - Prob. 55ECh. 4.5 - In Exercises 5356, rewrite the equation in terms...Ch. 4.5 - Nigeria has a growth rate of 0.025 or 2.5%....Ch. 4.5 - Prob. 58ECh. 4.5 - Prob. 59ECh. 4.5 - What is the half-life of a substance?Ch. 4.5 - Describe a difference between exponential growth...Ch. 4.5 - Describe the shape of a scatter plot that suggests...Ch. 4.5 - Prob. 63ECh. 4.5 - Would you prefer that your salary be modeled...Ch. 4.5 - Prob. 65ECh. 4.5 - Prob. 66ECh. 4.5 - Prob. 67ECh. 4.5 - In Example 1 on page 520, we used two data points...Ch. 4.5 - Prob. 69ECh. 4.5 - In Example 1 on page 520, we used two data points...Ch. 4.5 - Prob. 71ECh. 4.5 - Prob. 72ECh. 4.5 - Prob. 73ECh. 4.5 - Prob. 74ECh. 4.5 - Make Sense? In Exercises 7376, determine whether...Ch. 4.5 - Make Sense? In Exercises 7376, determine whether...Ch. 4.5 - The exponential growth models describe the...Ch. 4.5 - Prob. 78ECh. 4.5 - Prob. 79ECh. 4.5 - Prob. 80ECh. 4.5 - Prob. 81ECh. 4.5 - Exercises 8688 will help you prepare for the...Ch. 4.5 - Prob. 84ECh. 4.5 - Prob. 85ECh. 4 - In Exercises 1-5, graph f and g in the same...Ch. 4 - In Exercises 1-5, graph f and g in the same...Ch. 4 - In Exercises 1-5, graph f and g in the same...Ch. 4 - Prob. 4MCCh. 4 - Prob. 5MCCh. 4 - Prob. 6MCCh. 4 - Prob. 7MCCh. 4 - Prob. 8MCCh. 4 - Prob. 9MCCh. 4 - Prob. 10MCCh. 4 - Prob. 11MCCh. 4 - Prob. 12MCCh. 4 - In Exercises 10-20, evaluate each expression...Ch. 4 - Prob. 14MCCh. 4 - Prob. 15MCCh. 4 - Prob. 16MCCh. 4 - Prob. 17MCCh. 4 - In Exercises 10-20, evaluate each expression...Ch. 4 - Prob. 19MCCh. 4 - Prob. 20MCCh. 4 - Prob. 21MCCh. 4 - In Exercises 21-22, expand and evaluate numerical...Ch. 4 - Prob. 23MCCh. 4 - Prob. 24MCCh. 4 - Prob. 25MCCh. 4 - Use the formulas A=P(1+rn)nt and A=Pert to solve...Ch. 4 - Prob. 1RECh. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - In Exercises 59, graph f and g in the same...Ch. 4 - Prob. 9RECh. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 - Prob. 14RECh. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - In Exercises 1929, evaluate each expression...Ch. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - In Exercises 1929, evaluate each expression...Ch. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Prob. 33RECh. 4 - Prob. 34RECh. 4 - Prob. 35RECh. 4 - Prob. 36RECh. 4 - Prob. 37RECh. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 40RECh. 4 - Prob. 41RECh. 4 - Prob. 42RECh. 4 - Prob. 43RECh. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - Prob. 47RECh. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - In Exercises 5053, use properties of logarithms to...Ch. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - In Exercises 5859, use common logarithms or...Ch. 4 - In Exercises 5859, use common logarithms or...Ch. 4 - Prob. 60RECh. 4 - Prob. 61RECh. 4 - Prob. 62RECh. 4 - Prob. 63RECh. 4 - Prob. 64RECh. 4 - Prob. 65RECh. 4 - Prob. 66RECh. 4 - Prob. 67RECh. 4 - In Exercises 6473, solve each exponential...Ch. 4 - Prob. 69RECh. 4 - Prob. 70RECh. 4 - Prob. 71RECh. 4 - Prob. 72RECh. 4 - Prob. 73RECh. 4 - Prob. 74RECh. 4 - Prob. 75RECh. 4 - Prob. 76RECh. 4 - In Exercises 74-79, solve each logarithmic...Ch. 4 - Prob. 78RECh. 4 - Prob. 79RECh. 4 - Prob. 80RECh. 4 - Prob. 81RECh. 4 - Prob. 82RECh. 4 - Prob. 83RECh. 4 - Prob. 84RECh. 4 - Prob. 85RECh. 4 - Prob. 86RECh. 4 - Prob. 87RECh. 4 - Prob. 88RECh. 4 - Prob. 89RECh. 4 - Prob. 90RECh. 4 - Prob. 91RECh. 4 - Prob. 92RECh. 4 - Prob. 93RECh. 4 - Prob. 94RECh. 4 - Prob. 1TCh. 4 - Prob. 2TCh. 4 - Prob. 3TCh. 4 - Prob. 4TCh. 4 - Prob. 5TCh. 4 - Prob. 6TCh. 4 - Prob. 7TCh. 4 - Prob. 8TCh. 4 - Prob. 9TCh. 4 - Prob. 10TCh. 4 - Prob. 11TCh. 4 - Prob. 12TCh. 4 - Prob. 13TCh. 4 - Prob. 14TCh. 4 - Prob. 15TCh. 4 - Prob. 16TCh. 4 - Prob. 17TCh. 4 - Prob. 18TCh. 4 - Prob. 19TCh. 4 - Prob. 20TCh. 4 - Prob. 21TCh. 4 - Prob. 22TCh. 4 - Use the compound interest formulas to solve...Ch. 4 - Prob. 24TCh. 4 - Prob. 25TCh. 4 - The function A=82.3e0.004t models the population...Ch. 4 - Prob. 27TCh. 4 - Use the exponential decay model, A = A0ekt, to...Ch. 4 - Prob. 29TCh. 4 - Prob. 30TCh. 4 - Prob. 31TCh. 4 - Prob. 32TCh. 4 - Prob. 33TCh. 4 - Prob. 34TCh. 4 - Prob. 1CURCh. 4 - Prob. 2CURCh. 4 - Prob. 3CURCh. 4 - Prob. 4CURCh. 4 - Prob. 5CURCh. 4 - Prob. 6CURCh. 4 - Prob. 7CURCh. 4 - Prob. 8CURCh. 4 - Prob. 9CURCh. 4 - Prob. 10CURCh. 4 - Prob. 11CURCh. 4 - Prob. 12CURCh. 4 - Prob. 13CURCh. 4 - Prob. 14CURCh. 4 - Prob. 15CURCh. 4 - Prob. 16CURCh. 4 - you discover that the umber of hours you sleep...Ch. 4 - Prob. 18CURCh. 4 - Prob. 19CURCh. 4 - Prob. 20CUR
Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
SEE MORE TEXTBOOKS
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License