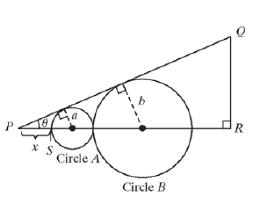
Problem 1SP: Let p5,7 be a point on the terminal side of angle drawn in standard position. Find the values of... Problem 2SP: Find the reference angle . a. =150 b. =157.5 c. =5 d. =133 Problem 3SP: Evaluate the functions. a. cos56 b. cot120 c. csc74 Problem 4SP: Evaluate the functions. a. csc11 b. cos600 Problem 5SP: Given cos=38 and sin0 , find and tan . Problem 6SP: Given sin=513 for in Quadrant IV, find cos , and tan . Problem 1PE: The distance from the origin to a point Px,y is given by . Problem 2PE Problem 3PE: If is an angle in standard position, the angle for is the acute angle formed by the terminal... Problem 4PE: The values tan and sec are undefined for odd multiples of . Problem 5PE: The values cot and csc are undefined for multiples of . Problem 6PE: For what values of is sin greater than 1 ? Problem 7PE: Let px,y be a point on the terminal side of an angle drawn in standard position and let r be the... Problem 8PE: Fill in the cells in the table with the appropriate sign for each trigonometric function for in... Problem 9PE: For Exercises 9-14, given the stated conditions, identify the quadrant in which lies. sin0 and tan0 Problem 10PE: For Exercises 9-14, given the stated conditions, identify the quadrant in which lies. csc0 and cot0 Problem 11PE Problem 12PE: For Exercises 9-14, given the stated conditions, identify the quadrant in which lies. cot0 and sin0 Problem 13PE: For Exercises 9-14, given the stated conditions, identify the quadrant in which lies. cos0 and cot0 Problem 14PE: For Exercises 9-14, given the stated conditions, identify the quadrant in which lies. cot0 and sec0 Problem 15PE Problem 16PE: For Exercises 15-20, a point is given on the terminal side of an angle drawn in standard position.... Problem 17PE: For Exercises 15-20, a point is given on the terminal side of an angle drawn in standard position.... Problem 18PE: For Exercises 15-20, a point is given on the terminal side of an angle drawn in standard position.... Problem 19PE: For Exercises 15-20, a point is given on the terminal side of an angle drawn in standard position.... Problem 20PE: For Exercises 15-20, a point is given on the terminal side of an angle drawn in standard position.... Problem 21PE: Complete the table for the given angles. Problem 22PE Problem 23PE: For Exercises 23-30, find the reference angle for the given angle. (See Example 2) a. 135 b. 330 c.... Problem 24PE: For Exercises 23-30, find the reference angle for the given angle. (See Example 2) a. 120 b. 225 c.... Problem 25PE: For Exercises 23-30, find the reference angle for the given angle. (See Example 2) a. 23 b. 56 c.... Problem 26PE: For Exercises 23-30, find the reference angle for the given angle. (See Example 2) a. 54 b. 116 c.... Problem 27PE: For Exercises 23-30, find the reference angle for the given angle. (See Example 2) a. 2017 b. 9920... Problem 28PE Problem 29PE: For Exercises 23-30, find the reference angle for the given angle. (See Example 2) a. 1.8 b. 1.8 c.... Problem 30PE: For Exercises 23-30, find the reference angle for the given angle. (See Example 2) a. 0.6 b. 0.6 c.... Problem 31PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) sin120 Problem 32PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) cos225 Problem 33PE Problem 34PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) sin56 Problem 35PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) sec330 Problem 36PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) csc225 Problem 37PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) sec133 Problem 38PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) csc53 Problem 39PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) cot240 Problem 40PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) tan150 Problem 41PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) tan54 Problem 42PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) cot34 Problem 43PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) cos630 Problem 44PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) sin630 Problem 45PE Problem 46PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) cos114 Problem 47PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) sec1170 Problem 48PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) csc750 Problem 49PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) csc5 Problem 50PE Problem 51PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) tan2400 Problem 52PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) cot900 Problem 53PE Problem 54PE: For Exercises 31-54, use reference angles to find the exact value. (See Examples 3 and 4) tan184 Problem 55PE: For Exercises 55-58, find two angles between 0 and 360 for the given condition. sin=12 Problem 56PE: For Exercises 55-58, find two angles between 0 and 360 for the given condition. cos=22 Problem 57PE: For Exercises 55-58, find two angles between 0 and 360 for the given condition. cot=3 Problem 58PE Problem 59PE: For Exercises 59-62, find two angles between 0 and 2 for the given condition. sec=2 Problem 60PE Problem 61PE: For Exercises 59-62, find two angles between 0 and 2 for the given condition. tan=33 Problem 62PE: For Exercises 59-62, find two angles between 0 and 2 for the given condition. cot=1 Problem 63PE: In Exercises 63-68, find the values of the trigonometric functions from the given information. (See... Problem 64PE: In Exercises 63-68, find the values of the trigonometric functions from the given information. (See... Problem 65PE: In Exercises 63-68, find the values of the trigonometric functions from the given information. (See... Problem 66PE: In Exercises 63-68, find the values of the trigonometric functions from the given information. (See... Problem 67PE: In Exercises 63-68, find the values of the trigonometric functions from the given information. (See... Problem 68PE: In Exercises 63-68, find the values of the trigonometric functions from the given information (See... Problem 69PE Problem 70PE: For Exercises 69-74, use fundamental trigonometric identities to find the values of the functions.... Problem 71PE: For Exercises 69-74, use fundamental trigonometric identities to find the values of the functions.... Problem 72PE: For Exercises 69-74, use fundamental trigonometric identities to find the values of the functions.... Problem 73PE Problem 74PE: For Exercises 69-74, use fundamental trigonometric identities to find the values of the functions.... Problem 75PE Problem 76PE: For Exercises 75-76, find the sign of the expression for in each quadrant. Problem 77PE: For Exercises 77-84, suppose that is an acute angle. Identify each statement as true or false. If... Problem 78PE: For Exercises 77-84, suppose that is an acute angle. Identify each statement as true or false. If... Problem 79PE: For Exercises 77-84, suppose that is an acute angle. Identify each statement as true or false. If... Problem 80PE: For Exercises 77-84, suppose that is an acute angle. Identify each statement as true or false. If... Problem 81PE: For Exercises 77-84, suppose that is an acute angle. Identify each statement as true or false. If... Problem 82PE Problem 83PE Problem 84PE: For Exercises 77-84, suppose that is an acute angle. Identify each statement as true or false. If... Problem 85PE: For Exercises 85-90, find the value of each expression. sin30cos150sec60csc120 Problem 86PE: For Exercises 85-90, find the value of each expression. cos45sin240tan135cot60 Problem 87PE Problem 88PE Problem 89PE: For Exercises 85-90, find the value of each expression. 2tan1161tan2116 Problem 90PE Problem 91PE Problem 92PE: For Exercises 91-94, verify the statement for the given values. cosBA=cosBcosA+sinBsinA;A=330,B=120 Problem 93PE: For Exercises 91-94, verify the statement for the given values.... Problem 94PE: For Exercises 91-94, verify the statement for the given values.... Problem 95PE: For Exercises 95-96, give the exact values if possible. Otherwise, use a calculator and approximate... Problem 96PE: For Exercises 95-96, give the exact values if possible. Otherwise, use a calculator and approximate... Problem 97PE: Explain why neither sinnorcos can be greater than 1 . Refer to the figure for your explanation. Problem 98PE: Explain why tan is undefined at =2 but cot is defined at =2 . Problem 99PE Problem 100PE: The circle shown is centered at the origin with a radius of 1 . The segment BD is tangent to the... Problem 101PE: Circle A, with radius a, and circle B , with radius b , are tangent to each other and to PQ (see... format_list_bulleted


 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning




