
Concept explainers
(a)
To Write: The conditional statement that shows the relationship between the areas of a pair of congruent
(a)
Answer to Problem 33PPS
If triangles are congruent, then they have the same area.
Explanation of Solution
Given information: The given statement is “the areas of congruent triangles are equal”.
As we know that congruent triangles have the same sides and equal three
Therefore, the two triangles will have the same area.
Hence, the conditional statement is ‘If triangles are congruent, then they have the same area’.
(b)
To explain: Whether the converse of conditional statement is true or false.
(b)
Answer to Problem 33PPS
The converse condition of conditional statement is false.
Explanation of Solution
Given information: If triangles are congruent, then they have the same area.
The converse of the conditional statement ‘If triangles are congruent, then they have the same area’ is ‘the triangles have the same area when they are congruent’.
We can see that these are false because two triangles can have the same area but can’t be congruent, depicted below.
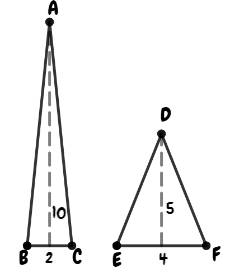
Area of the first triangle,
Area of the second triangle,
Thus,
(c)
To explain: The possibility of two equilateral triangles can have the same area but are not congruent.
(c)
Answer to Problem 33PPS
It is impossible to have two non congruent equilateral triangles with the same areas.
Explanation of Solution
Given information: Two equilateral triangles are given.
Two non congruent triangles can’t have the same area because their side’s length and angles not equal.
(d)
To explain: The possibility of two rectangles can have the same area but are not congruent.
(d)
Answer to Problem 33PPS
Yes! It is possible to have two non congruent rectangles with the same area.
Explanation of Solution
Given information: Two non congruent rectangles are given.
Two non congruent triangles can have the same area.
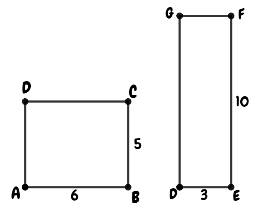
But, we can see from the sketch that sides are not congruent.
Therefore,
(e)
To explain: The possibility of two squares can have the same area but are not congruent.
(e)
Answer to Problem 33PPS
No! It is not possible to have two non congruent squares with the same area.
Explanation of Solution
Given information: Two non congruent squares are given.
Two non congruent squares can’t have the same area.
As we know,
Where, s is side of square.
If the sides of the squares are equal, then its area will be equal. In this condition, its sides also become congruent.
Hence, it is not possible to draw two non congruent squares with the same area.
(f)
To find: The
(f)
Answer to Problem 33PPS
The given conditional statement is valid for regular polygons.
Explanation of Solution
Given information: The conditional statement is given, If a pair of ……. Are congruent, then they have the same area.
The given condition will be true only for equilateral triangle, squares and shapes that have all sides of the same length.
Therefore, we can say that it is valid for regular polygon.
Chapter 4 Solutions
Glencoe Geometry Student Edition C2014
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Algebra and Trigonometry (6th Edition)
University Calculus: Early Transcendentals (4th Edition)
Elementary Statistics: Picturing the World (7th Edition)
- Proof: LN⎯⎯⎯⎯⎯LN¯ divides quadrilateral KLMN into two triangles. The sum of the angle measures in each triangle is ˚, so the sum of the angle measures for both triangles is ˚. So, m∠K+m∠L+m∠M+m∠N=m∠K+m∠L+m∠M+m∠N=˚. Because ∠K≅∠M∠K≅∠M and ∠N≅∠L, m∠K=m∠M∠N≅∠L, m∠K=m∠M and m∠N=m∠Lm∠N=m∠L by the definition of congruence. By the Substitution Property of Equality, m∠K+m∠L+m∠K+m∠L=m∠K+m∠L+m∠K+m∠L=°,°, so (m∠K)+ m∠K+ (m∠L)= m∠L= ˚. Dividing each side by gives m∠K+m∠L=m∠K+m∠L= °.°. The consecutive angles are supplementary, so KN⎯⎯⎯⎯⎯⎯∥LM⎯⎯⎯⎯⎯⎯KN¯∥LM¯ by the Converse of the Consecutive Interior Angles Theorem. Likewise, (m∠K)+m∠K+ (m∠N)=m∠N= ˚, or m∠K+m∠N=m∠K+m∠N= ˚. So these consecutive angles are supplementary and KL⎯⎯⎯⎯⎯∥NM⎯⎯⎯⎯⎯⎯KL¯∥NM¯ by the Converse of the Consecutive Interior Angles Theorem. Opposite sides are parallel, so quadrilateral KLMN is a parallelogram.arrow_forwardQuadrilateral BCDE is similar to quadrilateral FGHI. Find the measure of side FG. Round your answer to the nearest tenth if necessary. BCDEFGHI2737.55arrow_forwardAn angle measures 70.6° more than the measure of its supplementary angle. What is the measure of each angle?arrow_forward
- Name: Date: Per: Unit 7: Geometry Homework 4: Parallel Lines & Transversals **This is a 2-page document! ** Directions: Classify each angle pair and indicate whether they are congruent or supplementary. 1 1.23 and 25 2. 24 and 28 3. 22 and 25 4. 22 and 28 5. 21 and 27 6. 22 and 26 Directions: Find each angle measure. 7. Given: wvm25-149 m21- 8. Given: mn: m1=74 mz2- m22- m.23- m23- mz4= V mz4= m25= m26- m26= m27- m27 m28- m48= 9. Given: a || b: m28 125 m2- 10. Given: xy: m22-22 m21- = mz2- m43- m3- mZA m24-> m. 5- m25- m26- m.26=> m2]=> m27= m28- 11. Given: rm2-29: m15-65 m2=> m29-> m3- m. 10- mc4= m25= m212- m.46- m213- mat- m214- m28- & Gina when (N) Things ALICE 2017arrow_forwardMatch each statement to the set of shapes that best describes them. 1. Similar triangles by SSS 2. Similar triangles by SAS 3. Similar triangles by AA 4. The triangles are not similar > U E 35° 89° S F 89° J 35° 94° G 52° 90° E K 52° Iarrow_forwardMatch each transformation series with the diagram that applies to it. 1. (x, y) (x-10, y + 7) scale factor: 2 2. (x, y)(x-8, y+6) scale factor: 4 3. (x, y)(x+1, y - 5) scale factor: 5 D' 104º 6 2 -10 8 -6 F2 4 5 D 2 E -4 -6 100 E 8 10 Farrow_forward
- Which sets of figures below are similar? Select all that apply. 48 yd 48 yd G 48 yd 26 mm 40 m 23 km 25 m 22 mm 37 mm 25 mi 42 yd 48 yd 48 yd 48 yd U 42 yd 25 mm M T 40 mi 20 mm 25 mm 30 mi 48 m K 37 mm 20 mm 48 m S 30 mi 73 km 29 km 29 kmarrow_forwardGHUK PTSRQ. What is mz J? H Q I 77° 102° G 77° K J R 135° P T 123° Sarrow_forwardSolve it correctly and in Frencharrow_forward
- A rug company weaves rugs that are made by repeating the design in Figure 12.49. Lengths of portions of the design are indicated in the figure. The yarn for the shaded portion of the design costs $5 per square unit, and the yarn for the unshaded portion of the design costs $3 per square unit. How much will the yarn for a 60-unit-by-84-unit rug cost? Explain your reasoning.arrow_forward11:18 91 chisholminstitute.bksblive2.com.au 1.5 ACSF L5 SC Geometry and Measure: Pythagorus' Theorum Pythagorean Problems Calculate the lengths of all of this triangle's sides. x = 64 cm² y A ↑ ४ 225 cm² + ? Image not drawn accurately. 45 45arrow_forwardWhat is WX explain your reasoningarrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

