Chapter 4.3, Problem 1E

To determine

To calculate: For the function, $f\left(x\right)=5-7x-4x^2$ , the local extrema, the intervals in which the function is increasing or decreasing and sketch the graph of the function.

Answer to Problem 1E

The function $f\left(x\right)=5-7x-4x^2$ is increasing on the interval $\left(-\infty ,-\frac{7}{8}\right]$, decreasing on the interval $\left[-\frac{7}{8},\infty \right)$and local maximum value is, $f\left(-\frac{7}{8}\right)=\frac{129}{16}$. The graph of the function is,

  

Explanation of Solution

Given information:

The function, $f\left(x\right)=5-7x-4x^2$ .

Formula used:

Let a function g be continuous on closed interval $\left[c,d\right]$ and differentiable on open interval $\left(c,d\right)$ ,

If first derivative of the function is greater than zero that is $g\text{'}\left(x\right)>0$ for every xin $\left(c,d\right)$ , then the function g is increasing on interval $\left[c,d\right]$ .

If first derivative of the function is less than zero that is $g\text{'}\left(x\right)<0$ for every xin $\left(c,d\right)$ , then the function g is decreasing on interval $\left[c,d\right]$ .

If a is a critical number for the function g, then local extrema are as follows,

If first derivative of the function that is $g\text{'}$ changes it sign from positive to negative at a , then $g\left(a\right)$ is called local maximum of g .

If first derivative of the function that is $g\text{'}$ changes it sign from negative to positive at a , then $g\left(a\right)$ is called local minimum of g .

If $g\text{'}\left(x\right)>0$ or $g\text{'}\left(x\right)<0$ for every x in $\left(c,d\right)$ except $x=a$ , then $g\left(a\right)$ is not a local extreum of g .

Calculation:

Consider the function, $f\left(x\right)=5-7x-4x^2$ .

Differentiate the function with respect to x ,

  $\begin{array}{c}f\text{'}\left(x\right)=\frac{d}{dx}\left(5-7x-4x^2\right)\\ =-7-8x\end{array}$

Equate the derivative obtained above to 0 to get the critical number for the function,

  $\begin{array}{c}-7-8x=0\\ x=-\frac{7}{8}\end{array}$

Therefore, critical point is $x=-\frac{7}{8}$ .

Since the function is polynomial, construct the open intervals to test the increasing and decreasing nature of the function, $\left(-\infty ,-\frac{7}{8}\right)$ and $\left(-\frac{7}{8},\infty \right)$ .

Observe that on the above two intervals, the derivative function has no zeros, and is continuous.

Therefore, the function $f\text{'}\left(x\right)$ has same sign throughout the interval.

Consider the interval, $\left(-\infty ,-\frac{7}{8}\right)$ . Choose any number that lies in between the interval, say $k=-1$ .

Recall if a function g is continuous on closed interval $\left[c,d\right]$ and differentiable on open interval $\left(c,d\right)$ ,

If first derivative of the function is greater than zero that is $g\text{'}\left(x\right)>0$ for every xin $\left(c,d\right)$ , then the function g is increasing on interval $\left[c,d\right]$ .

If first derivative of the function is less than zero that is $g\text{'}\left(x\right)<0$ for every xin $\left(c,d\right)$ , then the function g is decreasing on interval $\left[c,d\right]$ .

Apply it, substitute $k=-1$ , in the $f\text{'}\left(x\right)$ and check the value,

  $\begin{array}{c}f\text{'}\left(-1\right)=-7-8\left(-1\right)\\ =-7+8\\ =1\end{array}$

Since the obtained value is greater than 0, that is $f\text{'}\left(x\right)>0$ , the function $f\left(x\right)=5-7x-4x^2$ is increasing on interval $\left(-\infty ,-\frac{7}{8}\right]$ .

Next, consider the interval, $\left(-\frac{7}{8},\infty \right)$ . Choose any number that lies in between the interval, say $k=1$ .

Apply it, substitute $k=1$ , in the $f\text{'}\left(x\right)$ and check the value,

  $\begin{array}{c}f\text{'}\left(-1\right)=-7-8\left(1\right)\\ =-7-8\\ =-15\end{array}$

Since the obtained value is less than 0, that is $f\text{'}\left(x\right)<0$ , the function $f\left(x\right)=5-7x-4x^2$ is decreasing on interval $\left[-\frac{7}{8},\infty \right)$ .

The above statements are summarized as,

  $\begin{array}{ccc}\text{Interval}& \left(-\infty ,-\frac{7}{8}\right)& \left(-\frac{7}{8},\infty \right)\\ k& -1& 1\\ \text{Test value }f\text{'}\left(k\right)& 1& -15\\ \text{Sign value of }f\text{'}\left(k\right)& +& -\\ \text{Conclusion}& \text{increasing}& \text{decreasing}\end{array}$

Recall, if a is a critical number for the function g, then local extrema are as follows,

If first derivative of the function that is $g\text{'}$ changes it sign from positive to negative at a , then $g\left(a\right)$ is called local maximum of g .

If first derivative of the function that is $g\text{'}$ changes it sign from negative to positive at a , then $g\left(a\right)$ is called local minimum of g .

If $g\text{'}\left(x\right)>0$ or $g\text{'}\left(x\right)<0$ for every x in $\left(c,d\right)$ except $x=a$ , then $g\left(a\right)$ is not a local extreum of g .

Since, the function $f\text{'}\left(x\right)$ changes it sign from positive to negative at the critical point $x=-\frac{7}{8}$ , so by first derivative the function $f\left(x\right)$ has local maxima at $x=-\frac{7}{8}$ .

Value of the function at $x=-\frac{7}{8}$ is, substitute the value in the function $f\left(x\right)=5-7x-4x^2$ .

  $\begin{array}{c}f\left(-\frac{7}{8}\right)=5-7\left(-\frac{7}{8}\right)-4{\left(-\frac{7}{8}\right)}^2\\ =5+\frac{49}{8}-\frac{49}{16}\\ =\frac{129}{16}\end{array}$

Therefore, local maximum value is, $f\left(-\frac{7}{8}\right)=\frac{129}{16}$ .

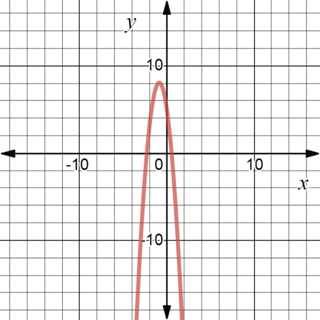
Last, to sketch the graph of the function, equate the function to 0, to evaluate the x -intercept of the function,

  $\begin{array}{c}0=5-7x-4x^2\\ 4x^2+7x-5=0\\ x=\frac{-7\pm \sqrt{7^2-4\left(4\right)\left(-5\right)}}{2\left(4\right)}\\ x=\frac{-7\pm \sqrt{49+80}}{8}\end{array}$

Simplify it further as,

  $x=\frac{-7\pm \sqrt{129}}{8}$

Therefore, x intercepts are $\left(\frac{-7+\sqrt{129}}{8},0\right)$ and $\left(\frac{-7-\sqrt{129}}{8},0\right)$ .

Evaluate the value of the function when x is zero, to find the y -intercept of the function,

  $\begin{array}{c}f\left(0\right)=5-7\left(0\right)-4{\left(0\right)}^2\\ =5\end{array}$

Therefore, y intercept is $\left(0,5\right)$ .

Plot all the points obtained above that is points that corresponds to critical numbers and intercepts to sketch the graph of the function, $\left(\frac{-7+\sqrt{129}}{8},0\right)$ , $\left(\frac{-7-\sqrt{129}}{8},0\right)$ , $\left(0,5\right)$ and $\left(-\frac{7}{8},\frac{129}{16}\right)$ .

The graph of the function $f\left(x\right)=5-7x-4x^2$ is provided below,

  

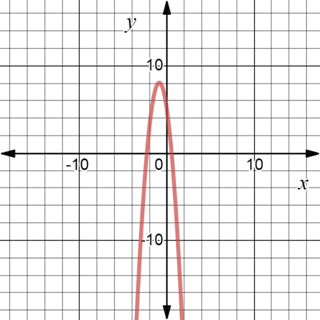
Thus, the function $f\left(x\right)=5-7x-4x^2$ is increasing on the interval $\left(-\infty ,-\frac{7}{8}\right]$ , decreasing on the interval $\left[-\frac{7}{8},\infty \right)$ and local maximum value is, $f\left(-\frac{7}{8}\right)=\frac{129}{16}$ .