Chapter 4.2, Problem 41E

The Trapezoidal Rule

We can approximate an integral by replacing each rectangle in a Riemann sun with a trapezoid. The area of a trapezoid is $h\left(c_1+c_2\right)/2$, where $c_1$ and $c_2$ are the lengths of the parallel sides and h is the distance between the sides. Thus,

Area under f over $\left[a,b\right]$

$\approx x\frac{f\left(a\right)=f\left(m\right)}{2}+x\frac{f\left(m\right)+f\left(b\right)}{2}$

$\approx x\left[\frac{f\left(a\right)}{2}+f\left(m\right)+\frac{f\left(b\right)}{2}\right]$.

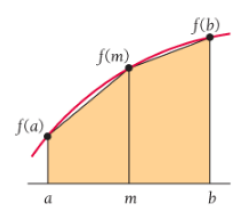
If $\left[a,b\right]$ is subdivided into n equal subintervals of length $x=\left(b-a\right)/n$, we have

Area under $f$

over $\left[a,b\right]$

$\approx x\left[\frac{f\left(x_1\right)}{2}+f\left(x_2\right)+f\left(x_3\right)+\cdot \cdot \cdot +f\left(x_n\right)+\frac{f\left(b\right)}{2}\right]$,

Where $x_1=a$ and $x_n=x_{n-1}+x\text{ or }{x}_n=a+\left(n-1\right)x$.

Use the Trapezoidal Rule and the interval subdivision of Exercise 18 (a) to approximate the area under the graph of

$f\left(x\right)=x^2+1\text{ over }\left[0.5\right]$