
Expand Your knowledge: Logarithmic Transformations. Exponential Growth Model There are several extensions of linear regression that apply to exponential growth and power law models. Problems 22-25 will outline some of these extensions. First of all. recall that a variable grows linearly over time if it adds a fixed increment during each equal period. Exponential growth occurs when a variable is multiplied by a fixed number during each period. This means that exponential growth increases by a fixed multiple or percentage of the previous amount. College algebra can be used to show that if a variable grows exponentially, then its logarithm grows linearly. The exponential growth model is
How do we know when we are dealing with exponential growth, and how can we estimate
| x | 1 | 2 | 3 | 4 | 5 |
| y | 3 | 12 | 22 | 51 | 145 |
Consider the following data, where x = time in hours and y = number of bacteria in a laboratory culture at the end of x hours.
(a) Look at the Excel graph of the
(b) Now consider a transformation
| x | 1 | 2 | 3 | 4 | 5 |
| y'=- log y | 0.477 | 1.079 | 1.342 | 1.748 | 2.161 |
Look at the Excel graph of the scatter diagram of the (x. y') data pairs and compare this diagram with the diagram in part (a). Which graph appears to better fit a straight line?
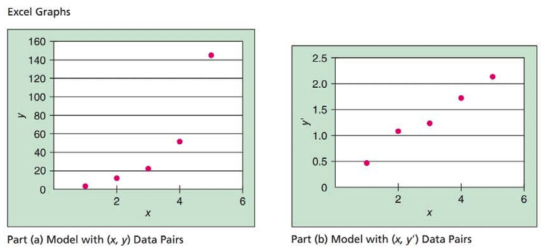
(c) Use a calculator with regression keys to verify the linear regression equation for the (x, y) data pairs,
(d) Use a calculator with regression keys to verify the linear regression equation for the (x, y') data pairs,
(e) The exponential growth model is
Note: The TI-84Plus/TI-83Plu.s/TI-nspire calculators fully support the exponential growth model. Place the original x data in list LI and the corresponding y data in list L2. Then press STAT, followed by CALC, and scroll down to option 0: ExpReg. The output gives values for
Want to see the full answer?
Check out a sample textbook solution
Chapter 4 Solutions
Bundle: Understanding Basic Statistics, Loose-leaf Version, 7th + WebAssign Printed Access Card for Brase/Brase's Understanding Basic Statistics, ... for Peck's Statistics: Learning from Data
- A company found that the daily sales revenue of its flagship product follows a normal distribution with a mean of $4500 and a standard deviation of $450. The company defines a "high-sales day" that is, any day with sales exceeding $4800. please provide a step by step on how to get the answers in excel Q: What percentage of days can the company expect to have "high-sales days" or sales greater than $4800? Q: What is the sales revenue threshold for the bottom 10% of days? (please note that 10% refers to the probability/area under bell curve towards the lower tail of bell curve) Provide answers in the yellow cellsarrow_forwardFind the critical value for a left-tailed test using the F distribution with a 0.025, degrees of freedom in the numerator=12, and degrees of freedom in the denominator = 50. A portion of the table of critical values of the F-distribution is provided. Click the icon to view the partial table of critical values of the F-distribution. What is the critical value? (Round to two decimal places as needed.)arrow_forwardA retail store manager claims that the average daily sales of the store are $1,500. You aim to test whether the actual average daily sales differ significantly from this claimed value. You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. Showing the calculation is a must. If calculation is missing,so please provide a step by step on the answers Numerical answers in the yellow cellsarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill

 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning





