Chapter 4.2, Problem 1P

For each diagram, find the relationship between the number of shapes and the perimeter of the figure they form. Represent this relationship using a table, words, an equation, and a graph.

To determine

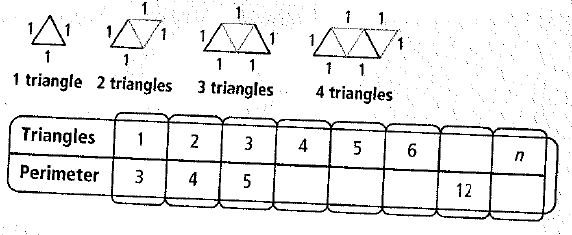
To find : The perimeter when the triangles are 4,5 and 6. Then we need to find the number of triangles when perimeter is 12. And we need to find the rule.

Answer to Problem 1P

  

Explanation of Solution

Given information: We are given with number of triangles and it’s perimeters as (1,3), (2,4),(3,5),….

Calculation:

If we see the y values , they are increasing by 1 when x values are increasing by 1.

So, according to this concept, when triangles =4, perimeter=6

When triangles =5, perimeter=7

When triangles =6, perimeter=8.

Now, use the same rule to find number of triangles when perimeter is 12.

Number of triangles	Perimeter
7	9
8	10
9	11
10	12

Now, let’s find the rule by finding the slope and y intercept.

Take (1,3) and (2,4)

Slope $m=\frac{4-3}{2-1}=1$

Plug in this value for ‘m’

We get y=1x+b

Use one of the points to get value for ‘b’

3=1(1) + b

3=1+ b

Subtract both sides 1

b =2

So, rule is y=x +2

Here we need to use ‘ n’ instead of x .

So, rule is n +2