College Algebra Essentials (5th Edition)
5th Edition
ISBN: 9780134469294
Author: Blitzer, Robert F.
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 4.1, Problem 72E
Use a calculator with an
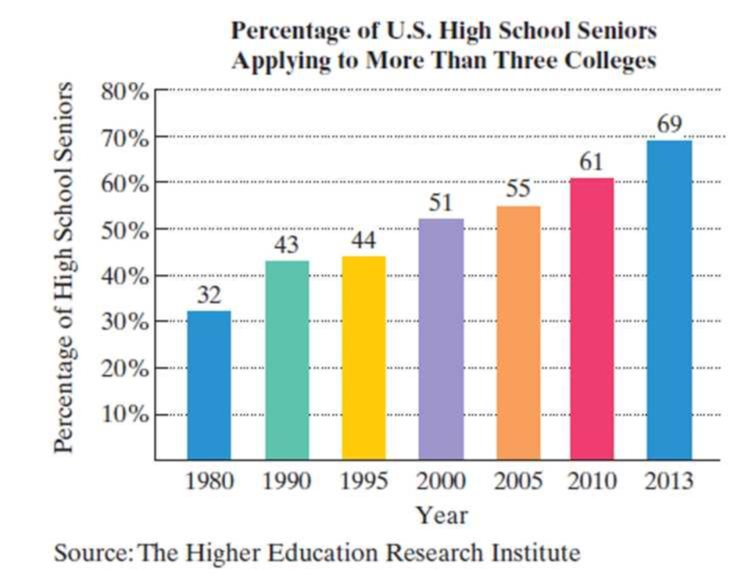
The bar graph shows the percentage of U.S. high school seniors who applied to more than three colleges for selected years from 1980 through 2013.
The data can be modeled by
in which f(x) and g(x) represent the percentage of high school seniors who applied to more than three colleges x years after 1980. Use these functions to solve Exercises 71–72. Where necessary, round answers to the nearest percent.
72. a. According to the linear model, what percentage of high school seniors applied to more than three colleges in 2010?
b. According to the exponential model, what percentage of high school seniors applied to more than three colleges in 2010?
c. Which function is a better model for the data shown by the bar graph in 2010?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
How long is a guy wire reaching from the top of a
15-foot pole to a point on the ground
9-feet from the pole?
Question content area bottom
Part 1
The guy wire is exactly
feet long.
(Type an exact answer, using radicals as needed.)
Part 2
The guy wire is approximatelyfeet long.
(Round to the nearest thousandth.)
Question 6
Not yet
answered
Marked out of
5.00
Flag question
=
If (4,6,-11) and (-12,-16,4),
=
Compute the cross product vx w
k
Consider the following vector field v^-> (x,y):
v^->(x,y)=2yi−xj
What is the magnitude of the vector v⃗ located in point (13,9)?
[Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places]
Chapter 4 Solutions
College Algebra Essentials (5th Edition)
Ch. 4.1 - Use the exponential function in Example l to find...Ch. 4.1 - Prob. 2CPCh. 4.1 - Prob. 3CPCh. 4.1 - Prob. 4CPCh. 4.1 - Prob. 5CPCh. 4.1 - Use f(x)=1145e0.0325x, the model described in...Ch. 4.1 - A sum of 10,000 is invested at an annual rate of...Ch. 4.1 - Prob. 1CVCCh. 4.1 - Prob. 2CVCCh. 4.1 - Fill in each blank so that the resulting statement...
Ch. 4.1 - Fill in each blank so that the resulting statement...Ch. 4.1 - Prob. 5CVCCh. 4.1 - Prob. 1ECh. 4.1 - Prob. 2ECh. 4.1 - Prob. 3ECh. 4.1 - Prob. 4ECh. 4.1 - Prob. 5ECh. 4.1 - In Exercises 110, approximate each number using a...Ch. 4.1 - Prob. 7ECh. 4.1 - Prob. 8ECh. 4.1 - Prob. 9ECh. 4.1 - Prob. 10ECh. 4.1 - Prob. 11ECh. 4.1 - In Exercises 1118, graph each function by making a...Ch. 4.1 - Prob. 13ECh. 4.1 - Prob. 14ECh. 4.1 - Prob. 15ECh. 4.1 - Prob. 16ECh. 4.1 - Prob. 17ECh. 4.1 - Prob. 18ECh. 4.1 - Prob. 19ECh. 4.1 - Prob. 20ECh. 4.1 - Prob. 21ECh. 4.1 - Prob. 22ECh. 4.1 - Prob. 23ECh. 4.1 - Prob. 24ECh. 4.1 - Prob. 25ECh. 4.1 - In Exercises 2534, begin by graphing f(x)=2x. Then...Ch. 4.1 - Prob. 27ECh. 4.1 - Prob. 28ECh. 4.1 - Prob. 29ECh. 4.1 - Prob. 30ECh. 4.1 - Prob. 31ECh. 4.1 - Prob. 32ECh. 4.1 - Prob. 33ECh. 4.1 - Prob. 34ECh. 4.1 - The figure shows the graph of f(x)=ex. In...Ch. 4.1 - The figure shows the graph of f(x)=ex. In...Ch. 4.1 - Prob. 37ECh. 4.1 - Prob. 38ECh. 4.1 - The figure shows the graph of f(x)=ex. In...Ch. 4.1 - Prob. 40ECh. 4.1 - Prob. 41ECh. 4.1 - Prob. 42ECh. 4.1 - Prob. 43ECh. 4.1 - Prob. 44ECh. 4.1 - The figure shows the graph of f(x)=ex. In...Ch. 4.1 - Prob. 46ECh. 4.1 - Prob. 47ECh. 4.1 - Prob. 48ECh. 4.1 - Prob. 49ECh. 4.1 - Prob. 50ECh. 4.1 - Prob. 51ECh. 4.1 - Prob. 52ECh. 4.1 - Use the compound interest formulas A=P(1+rn)nt and...Ch. 4.1 - Use the compound interest formulas A=P(1+rn)nt and...Ch. 4.1 - Prob. 55ECh. 4.1 - Prob. 56ECh. 4.1 - Prob. 57ECh. 4.1 - Prob. 58ECh. 4.1 - Prob. 59ECh. 4.1 - Prob. 60ECh. 4.1 - Prob. 61ECh. 4.1 - Prob. 62ECh. 4.1 - Prob. 63ECh. 4.1 - Prob. 64ECh. 4.1 - Prob. 65ECh. 4.1 - Prob. 66ECh. 4.1 - Prob. 67ECh. 4.1 - The formulas S=C(1+r)t models inflation, where C =...Ch. 4.1 - Prob. 69ECh. 4.1 - A decimal approximation for is 3.141593. Use a...Ch. 4.1 - Prob. 71ECh. 4.1 - Use a calculator with an ex key to solve Exercises...Ch. 4.1 - Use a calculator with an ex key to solve Exercises...Ch. 4.1 - Prob. 74ECh. 4.1 - The bar graph shows the percentage of people 25...Ch. 4.1 - Prob. 76ECh. 4.1 - Prob. 77ECh. 4.1 - Prob. 78ECh. 4.1 - Use a calculator to evaluate (1+1x)x for x = 10,...Ch. 4.1 - Prob. 80ECh. 4.1 - Prob. 81ECh. 4.1 - Prob. 82ECh. 4.1 - Prob. 83ECh. 4.1 - Make Sense? In Exercises 83-86, determine whether...Ch. 4.1 - Prob. 85ECh. 4.1 - Make Sense? In Exercises 83-86, determine whether...Ch. 4.1 - Prob. 87ECh. 4.1 - In Exercises 87-90, determine whether each...Ch. 4.1 - In Exercises 87-90, determine whether each...Ch. 4.1 - Prob. 90ECh. 4.1 - Prob. 91ECh. 4.1 - Prob. 92ECh. 4.1 - Prob. 93ECh. 4.1 - Prob. 94ECh. 4.1 - Prob. 95ECh. 4.1 - Prob. 96ECh. 4.1 - Prob. 97ECh. 4.1 - Prob. 98ECh. 4.1 - Prob. 99ECh. 4.2 - Check Point 1 Write each equation in its...Ch. 4.2 - Prob. 2CPCh. 4.2 - Prob. 3CPCh. 4.2 - Prob. 4CPCh. 4.2 - Prob. 5CPCh. 4.2 - Prob. 6CPCh. 4.2 - Prob. 7CPCh. 4.2 - Prob. 8CPCh. 4.2 - Use the formula in Example 9 to solve this...Ch. 4.2 - Prob. 10CPCh. 4.2 - Prob. 11CPCh. 4.2 - Prob. 1CVCCh. 4.2 - Prob. 2CVCCh. 4.2 - Prob. 3CVCCh. 4.2 - Prob. 4CVCCh. 4.2 - Prob. 5CVCCh. 4.2 - Prob. 6CVCCh. 4.2 - Prob. 7CVCCh. 4.2 - Prob. 8CVCCh. 4.2 - Prob. 9CVCCh. 4.2 - Prob. 10CVCCh. 4.2 - Prob. 11CVCCh. 4.2 - Prob. 12CVCCh. 4.2 - Prob. 13CVCCh. 4.2 - Prob. 14CVCCh. 4.2 - Prob. 15CVCCh. 4.2 - Prob. 1ECh. 4.2 - Prob. 2ECh. 4.2 - Prob. 3ECh. 4.2 - Prob. 4ECh. 4.2 - Prob. 5ECh. 4.2 - Prob. 6ECh. 4.2 - Prob. 7ECh. 4.2 - Prob. 8ECh. 4.2 - Prob. 9ECh. 4.2 - Prob. 10ECh. 4.2 - Prob. 11ECh. 4.2 - Prob. 12ECh. 4.2 - In Exercises 920, write each equation in its...Ch. 4.2 - Prob. 14ECh. 4.2 - Prob. 15ECh. 4.2 - Prob. 16ECh. 4.2 - Prob. 17ECh. 4.2 - Prob. 18ECh. 4.2 - Prob. 19ECh. 4.2 - Prob. 20ECh. 4.2 - Prob. 21ECh. 4.2 - Prob. 22ECh. 4.2 - Prob. 23ECh. 4.2 - Prob. 24ECh. 4.2 - Prob. 25ECh. 4.2 - Prob. 26ECh. 4.2 - Prob. 27ECh. 4.2 - In Exercises 2142, evaluate each expression...Ch. 4.2 - In Exercises 2142, evaluate each expression...Ch. 4.2 - Prob. 30ECh. 4.2 - Prob. 31ECh. 4.2 - Prob. 32ECh. 4.2 - Prob. 33ECh. 4.2 - Prob. 34ECh. 4.2 - Prob. 35ECh. 4.2 - Prob. 36ECh. 4.2 - Prob. 37ECh. 4.2 - Prob. 38ECh. 4.2 - Prob. 39ECh. 4.2 - Prob. 40ECh. 4.2 - Prob. 41ECh. 4.2 - Prob. 42ECh. 4.2 - Prob. 43ECh. 4.2 - Prob. 44ECh. 4.2 - Prob. 45ECh. 4.2 - Prob. 46ECh. 4.2 - Prob. 47ECh. 4.2 - Prob. 48ECh. 4.2 - Prob. 49ECh. 4.2 - Prob. 50ECh. 4.2 - Prob. 51ECh. 4.2 - Prob. 52ECh. 4.2 - Prob. 53ECh. 4.2 - Prob. 54ECh. 4.2 - Prob. 55ECh. 4.2 - Prob. 56ECh. 4.2 - Prob. 57ECh. 4.2 - Prob. 58ECh. 4.2 - Prob. 59ECh. 4.2 - Prob. 60ECh. 4.2 - Prob. 61ECh. 4.2 - Prob. 62ECh. 4.2 - Prob. 63ECh. 4.2 - Prob. 64ECh. 4.2 - Prob. 65ECh. 4.2 - Prob. 66ECh. 4.2 - Prob. 67ECh. 4.2 - Prob. 68ECh. 4.2 - Prob. 69ECh. 4.2 - Prob. 70ECh. 4.2 - Prob. 71ECh. 4.2 - Prob. 72ECh. 4.2 - Prob. 73ECh. 4.2 - The figure shows the graph of f(x) = ln x. In...Ch. 4.2 - Prob. 75ECh. 4.2 - Prob. 76ECh. 4.2 - Prob. 77ECh. 4.2 - Prob. 78ECh. 4.2 - Prob. 79ECh. 4.2 - Prob. 80ECh. 4.2 - Prob. 81ECh. 4.2 - In Exercises 81100, evaluate or simplify each...Ch. 4.2 - Prob. 83ECh. 4.2 - Prob. 84ECh. 4.2 - In Exercises 81100, evaluate or simplify each...Ch. 4.2 - In Exercises 81100, evaluate or simplify each...Ch. 4.2 - Prob. 87ECh. 4.2 - Prob. 88ECh. 4.2 - Prob. 89ECh. 4.2 - In Exercises 81100, evaluate or simplify each...Ch. 4.2 - Prob. 91ECh. 4.2 - Prob. 92ECh. 4.2 - Prob. 93ECh. 4.2 - Prob. 94ECh. 4.2 - Prob. 95ECh. 4.2 - Prob. 96ECh. 4.2 - Prob. 97ECh. 4.2 - Prob. 98ECh. 4.2 - Prob. 99ECh. 4.2 - Prob. 100ECh. 4.2 - Prob. 101ECh. 4.2 - Prob. 102ECh. 4.2 - Prob. 103ECh. 4.2 - Prob. 104ECh. 4.2 - Prob. 105ECh. 4.2 - Prob. 106ECh. 4.2 - Prob. 107ECh. 4.2 - Prob. 108ECh. 4.2 - Prob. 109ECh. 4.2 - Prob. 110ECh. 4.2 - Prob. 111ECh. 4.2 - Prob. 112ECh. 4.2 - Prob. 113ECh. 4.2 - Prob. 114ECh. 4.2 - Prob. 115ECh. 4.2 - Prob. 116ECh. 4.2 - Prob. 117ECh. 4.2 - Prob. 118ECh. 4.2 - Students in a psychology class took a final...Ch. 4.2 - Describe the relationship between an equation in...Ch. 4.2 - Prob. 121ECh. 4.2 - Prob. 122ECh. 4.2 - Describe the following property using words: logb...Ch. 4.2 - Prob. 124ECh. 4.2 - Prob. 125ECh. 4.2 - Prob. 126ECh. 4.2 - Prob. 127ECh. 4.2 - Prob. 128ECh. 4.2 - Prob. 129ECh. 4.2 - Prob. 130ECh. 4.2 - Prob. 131ECh. 4.2 - Prob. 132ECh. 4.2 - Prob. 133ECh. 4.2 - Prob. 134ECh. 4.2 - Prob. 135ECh. 4.2 - Make Sense? In Exercises 135138, determine whether...Ch. 4.2 - Prob. 137ECh. 4.2 - Prob. 138ECh. 4.2 - Prob. 139ECh. 4.2 - Prob. 140ECh. 4.2 - Prob. 141ECh. 4.2 - Prob. 142ECh. 4.2 - Prob. 143ECh. 4.2 - Without using a calculator, find the exact value...Ch. 4.2 - Prob. 145ECh. 4.2 - Prob. 146ECh. 4.2 - Prob. 147ECh. 4.2 - Prob. 148ECh. 4.2 - Prob. 149ECh. 4.2 - Prob. 150ECh. 4.2 - Exercises 150152 will help you prepare for the...Ch. 4.2 - Exercises 150152 will help you prepare for the...Ch. 4.3 - Prob. 1CPCh. 4.3 - Prob. 2CPCh. 4.3 - Prob. 3CPCh. 4.3 - Prob. 4CPCh. 4.3 - Prob. 5CPCh. 4.3 - Prob. 6CPCh. 4.3 - Prob. 7CPCh. 4.3 - Prob. 8CPCh. 4.3 - Prob. 1CVCCh. 4.3 - Prob. 2CVCCh. 4.3 - The power rule for logarithms states that logb M p...Ch. 4.3 - Prob. 4CVCCh. 4.3 - Prob. 1ECh. 4.3 - Prob. 2ECh. 4.3 - Prob. 3ECh. 4.3 - Prob. 4ECh. 4.3 - Prob. 5ECh. 4.3 - Prob. 6ECh. 4.3 - Prob. 7ECh. 4.3 - Prob. 8ECh. 4.3 - Prob. 9ECh. 4.3 - Prob. 10ECh. 4.3 - Prob. 11ECh. 4.3 - Prob. 12ECh. 4.3 - Prob. 13ECh. 4.3 - Prob. 14ECh. 4.3 - Prob. 15ECh. 4.3 - Prob. 16ECh. 4.3 - Prob. 17ECh. 4.3 - In Exercises 140, use properties of logarithms to...Ch. 4.3 - Prob. 19ECh. 4.3 - Prob. 20ECh. 4.3 - Prob. 21ECh. 4.3 - Prob. 22ECh. 4.3 - Prob. 23ECh. 4.3 - Prob. 24ECh. 4.3 - Prob. 25ECh. 4.3 - Prob. 26ECh. 4.3 - Prob. 27ECh. 4.3 - Prob. 28ECh. 4.3 - Prob. 29ECh. 4.3 - Prob. 30ECh. 4.3 - Prob. 31ECh. 4.3 - Prob. 32ECh. 4.3 - Prob. 33ECh. 4.3 - Prob. 34ECh. 4.3 - Prob. 35ECh. 4.3 - Prob. 36ECh. 4.3 - Prob. 37ECh. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - Prob. 40ECh. 4.3 - Prob. 41ECh. 4.3 - Prob. 42ECh. 4.3 - Prob. 43ECh. 4.3 - Prob. 44ECh. 4.3 - Prob. 45ECh. 4.3 - Prob. 46ECh. 4.3 - Prob. 47ECh. 4.3 - Prob. 48ECh. 4.3 - Prob. 49ECh. 4.3 - Prob. 50ECh. 4.3 - Prob. 51ECh. 4.3 - Prob. 52ECh. 4.3 - Prob. 53ECh. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Prob. 57ECh. 4.3 - Prob. 58ECh. 4.3 - Prob. 59ECh. 4.3 - Prob. 60ECh. 4.3 - In Exercises 4170, use properties of logarithms to...Ch. 4.3 - Prob. 62ECh. 4.3 - Prob. 63ECh. 4.3 - Prob. 64ECh. 4.3 - Prob. 65ECh. 4.3 - Prob. 66ECh. 4.3 - Prob. 67ECh. 4.3 - Prob. 68ECh. 4.3 - Prob. 69ECh. 4.3 - Prob. 70ECh. 4.3 - Prob. 71ECh. 4.3 - Prob. 72ECh. 4.3 - Prob. 73ECh. 4.3 - Prob. 74ECh. 4.3 - Prob. 75ECh. 4.3 - Prob. 76ECh. 4.3 - In Exercises 71-78, use common logarithms or...Ch. 4.3 - In Exercises 71-78, use common logarithms or...Ch. 4.3 - Prob. 79ECh. 4.3 - In Exercises 79-82, use a graphing utility and the...Ch. 4.3 - Prob. 81ECh. 4.3 - Prob. 82ECh. 4.3 - Prob. 83ECh. 4.3 - Prob. 84ECh. 4.3 - Prob. 85ECh. 4.3 - Prob. 86ECh. 4.3 - Prob. 87ECh. 4.3 - Prob. 88ECh. 4.3 - Prob. 89ECh. 4.3 - Prob. 90ECh. 4.3 - Prob. 91ECh. 4.3 - Prob. 92ECh. 4.3 - Prob. 93ECh. 4.3 - Prob. 94ECh. 4.3 - Prob. 95ECh. 4.3 - Prob. 96ECh. 4.3 - Prob. 97ECh. 4.3 - Prob. 98ECh. 4.3 - Prob. 99ECh. 4.3 - Prob. 100ECh. 4.3 - Prob. 101ECh. 4.3 - Prob. 102ECh. 4.3 - Prob. 103ECh. 4.3 - Prob. 104ECh. 4.3 - Prob. 105ECh. 4.3 - Prob. 106ECh. 4.3 - Prob. 107ECh. 4.3 - Prob. 108ECh. 4.3 - Prob. 109ECh. 4.3 - Prob. 110ECh. 4.3 - You overhear a student talking about a property of...Ch. 4.3 - Prob. 112ECh. 4.3 - Prob. 113ECh. 4.3 - Prob. 114ECh. 4.3 - Prob. 115ECh. 4.3 - Prob. 116ECh. 4.3 - Prob. 117ECh. 4.3 - Disprove each statement in Exercises 116120 by...Ch. 4.3 - Prob. 119ECh. 4.3 - Prob. 120ECh. 4.3 - Prob. 121ECh. 4.3 - Make Sense? In Exercises 121124, determine whether...Ch. 4.3 - Prob. 123ECh. 4.3 - Prob. 124ECh. 4.3 - Prob. 125ECh. 4.3 - Prob. 126ECh. 4.3 - In Exercises 125128, determine whether each...Ch. 4.3 - Prob. 128ECh. 4.3 - Prob. 129ECh. 4.3 - Prob. 130ECh. 4.3 - Prob. 131ECh. 4.3 - Prob. 132ECh. 4.3 - Prob. 133ECh. 4.3 - Prob. 134ECh. 4.3 - Prob. 135ECh. 4.3 - Prob. 136ECh. 4.3 - Prob. 137ECh. 4.3 - Prob. 138ECh. 4.3 - Prob. 139ECh. 4.4 - Solve: a. 53x6 = 125 b. 8x+2 = 4x3.Ch. 4.4 - Solve: a. 5x = 134 b. 10x = 8000.Ch. 4.4 - Solve: 7e2x 5 = 58. Find the solution set and...Ch. 4.4 - Prob. 4CPCh. 4.4 - Solve: e2x 8ex + 7 = 0. Find the solution set and...Ch. 4.4 - Prob. 6CPCh. 4.4 - Prob. 7CPCh. 4.4 - Prob. 8CPCh. 4.4 - Use the formula in Example 9 to answer this...Ch. 4.4 - How long, to the nearest tenth of a year, will it...Ch. 4.4 - Prob. 11CPCh. 4.4 - Fill in each blank so that the resulting statement...Ch. 4.4 - Prob. 2CVCCh. 4.4 - Prob. 3CVCCh. 4.4 - Fill in each blank so that the resulting statement...Ch. 4.4 - Prob. 5CVCCh. 4.4 - Prob. 6CVCCh. 4.4 - Prob. 7CVCCh. 4.4 - Prob. 8CVCCh. 4.4 - Fill in each blank so that the resulting statement...Ch. 4.4 - Fill in each blank so that the resulting statement...Ch. 4.4 - Prob. 11CVCCh. 4.4 - Prob. 1ECh. 4.4 - Prob. 2ECh. 4.4 - Prob. 3ECh. 4.4 - Prob. 4ECh. 4.4 - Prob. 5ECh. 4.4 - Prob. 6ECh. 4.4 - Prob. 7ECh. 4.4 - Prob. 8ECh. 4.4 - Prob. 9ECh. 4.4 - Prob. 10ECh. 4.4 - Prob. 11ECh. 4.4 - Prob. 12ECh. 4.4 - Prob. 13ECh. 4.4 - Prob. 14ECh. 4.4 - Prob. 15ECh. 4.4 - Prob. 16ECh. 4.4 - Prob. 17ECh. 4.4 - Prob. 18ECh. 4.4 - Prob. 19ECh. 4.4 - Prob. 20ECh. 4.4 - Prob. 21ECh. 4.4 - Prob. 22ECh. 4.4 - Prob. 23ECh. 4.4 - Prob. 24ECh. 4.4 - Prob. 25ECh. 4.4 - Prob. 26ECh. 4.4 - Prob. 27ECh. 4.4 - Prob. 28ECh. 4.4 - Prob. 29ECh. 4.4 - Prob. 30ECh. 4.4 - Prob. 31ECh. 4.4 - Prob. 32ECh. 4.4 - Prob. 33ECh. 4.4 - Prob. 34ECh. 4.4 - Prob. 35ECh. 4.4 - Prob. 36ECh. 4.4 - Prob. 37ECh. 4.4 - Prob. 38ECh. 4.4 - Solve each exponential equation in Exercises 2348....Ch. 4.4 - Prob. 40ECh. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Prob. 43ECh. 4.4 - Prob. 44ECh. 4.4 - Prob. 45ECh. 4.4 - Prob. 46ECh. 4.4 - Prob. 47ECh. 4.4 - Prob. 48ECh. 4.4 - Prob. 49ECh. 4.4 - Prob. 50ECh. 4.4 - Prob. 51ECh. 4.4 - Prob. 52ECh. 4.4 - Prob. 53ECh. 4.4 - Prob. 54ECh. 4.4 - Prob. 55ECh. 4.4 - Prob. 56ECh. 4.4 - Prob. 57ECh. 4.4 - Prob. 58ECh. 4.4 - Prob. 59ECh. 4.4 - Prob. 60ECh. 4.4 - Prob. 61ECh. 4.4 - Prob. 62ECh. 4.4 - Prob. 63ECh. 4.4 - Prob. 64ECh. 4.4 - Prob. 65ECh. 4.4 - Prob. 66ECh. 4.4 - Prob. 67ECh. 4.4 - Prob. 68ECh. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Prob. 70ECh. 4.4 - Prob. 71ECh. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Prob. 76ECh. 4.4 - Prob. 77ECh. 4.4 - Prob. 78ECh. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Prob. 80ECh. 4.4 - Prob. 81ECh. 4.4 - Prob. 82ECh. 4.4 - Prob. 83ECh. 4.4 - Prob. 84ECh. 4.4 - Prob. 85ECh. 4.4 - Prob. 86ECh. 4.4 - Prob. 87ECh. 4.4 - Prob. 88ECh. 4.4 - Prob. 89ECh. 4.4 - Solve each logarithmic equation in Exercises 4992....Ch. 4.4 - Prob. 91ECh. 4.4 - Prob. 92ECh. 4.4 - Prob. 93ECh. 4.4 - Prob. 94ECh. 4.4 - Prob. 95ECh. 4.4 - Prob. 96ECh. 4.4 - Prob. 97ECh. 4.4 - Prob. 98ECh. 4.4 - Prob. 99ECh. 4.4 - In Exercises 93102, solve each equation....Ch. 4.4 - In Exercises 93102, solve each equation....Ch. 4.4 - In Exercises 93102, solve each equation....Ch. 4.4 - Prob. 103ECh. 4.4 - The formula A=25.1e0.0187t models the population...Ch. 4.4 - Prob. 105ECh. 4.4 - Prob. 106ECh. 4.4 - Prob. 107ECh. 4.4 - Prob. 108ECh. 4.4 - Prob. 109ECh. 4.4 - Prob. 110ECh. 4.4 - Prob. 111ECh. 4.4 - Prob. 112ECh. 4.4 - In Exercises 111-114, complete the table for a...Ch. 4.4 - Prob. 114ECh. 4.4 - Prob. 115ECh. 4.4 - Prob. 116ECh. 4.4 - Prob. 117ECh. 4.4 - Prob. 118ECh. 4.4 - Prob. 119ECh. 4.4 - Prob. 120ECh. 4.4 - Prob. 121ECh. 4.4 - Prob. 122ECh. 4.4 - Prob. 123ECh. 4.4 - Prob. 124ECh. 4.4 - Prob. 125ECh. 4.4 - In Exercises 125-132, use your graphing utility to...Ch. 4.4 - Prob. 127ECh. 4.4 - Prob. 128ECh. 4.4 - Prob. 129ECh. 4.4 - Prob. 130ECh. 4.4 - In Exercises 125-132, use your graphing utility to...Ch. 4.4 - Prob. 132ECh. 4.4 - Prob. 133ECh. 4.4 - Prob. 137ECh. 4.4 - Prob. 138ECh. 4.4 - Prob. 139ECh. 4.4 - Make Sense? In Exercises 137140, determine whether...Ch. 4.4 - Prob. 141ECh. 4.4 - Prob. 142ECh. 4.4 - Prob. 143ECh. 4.4 - Prob. 144ECh. 4.4 - Prob. 145ECh. 4.4 - Prob. 146ECh. 4.4 - Prob. 147ECh. 4.4 - Prob. 148ECh. 4.4 - Use the graph of f to determine each of the...Ch. 4.4 - Prob. 151ECh. 4.4 - Prob. 152ECh. 4.4 - Prob. 153ECh. 4.4 - Exercises 153155 will help you prepare for the...Ch. 4.4 - U.S. soldiers fight Russian troops who have...Ch. 4.5 - In 2000, the population of Africa was 807 million...Ch. 4.5 - Prob. 2CPCh. 4.5 - Prob. 3CPCh. 4.5 - Table 4.7 shows the populations of various cities,...Ch. 4.5 - Prob. 5CPCh. 4.5 - Use the models f(x) = 0.074x + 2.294 and g(x) =...Ch. 4.5 - Rewrite y = 4(7.8)x in terms of base e. Express...Ch. 4.5 - Fill in each blank so that the resulting statement...Ch. 4.5 - Fill in each blank so that the resulting statement...Ch. 4.5 - Fill in each blank so that the resulting statement...Ch. 4.5 - For each of the scatter plots in Exercises 46,...Ch. 4.5 - For each of the scatter plots in Exercises 46,...Ch. 4.5 - For each of the scatter plots in Exercises 46,...Ch. 4.5 - Fill in each blank so that the resulting statement...Ch. 4.5 - Prob. 1ECh. 4.5 - Prob. 2ECh. 4.5 - Prob. 3ECh. 4.5 - The exponential models describe the population of...Ch. 4.5 - The exponential models describe the population of...Ch. 4.5 - Prob. 6ECh. 4.5 - Prob. 7ECh. 4.5 - About the size of New Jersey, Israel has seen its...Ch. 4.5 - Prob. 9ECh. 4.5 - In Exercises 9-14, complete the table. Round...Ch. 4.5 - Prob. 11ECh. 4.5 - Prob. 12ECh. 4.5 - Prob. 13ECh. 4.5 - Prob. 14ECh. 4.5 - Prob. 15ECh. 4.5 - Prob. 16ECh. 4.5 - Prob. 17ECh. 4.5 - Prob. 18ECh. 4.5 - Prob. 19ECh. 4.5 - Prob. 20ECh. 4.5 - Prob. 21ECh. 4.5 - Prob. 22ECh. 4.5 - Prob. 23ECh. 4.5 - Prob. 24ECh. 4.5 - In Exercises 21-26, complete the table. Round...Ch. 4.5 - Prob. 26ECh. 4.5 - Prob. 27ECh. 4.5 - Use the exponential decay model, A = A0ekt, to...Ch. 4.5 - Prob. 29ECh. 4.5 - Prob. 30ECh. 4.5 - Prob. 31ECh. 4.5 - Prob. 32ECh. 4.5 - Prob. 33ECh. 4.5 - Prob. 34ECh. 4.5 - Prob. 35ECh. 4.5 - Prob. 36ECh. 4.5 - Prob. 37ECh. 4.5 - Prob. 38ECh. 4.5 - We see from the calculator screen at the bottom of...Ch. 4.5 - We see from the calculator screen at the bottom of...Ch. 4.5 - We see from the calculator screen at the bottom of...Ch. 4.5 - Prob. 42ECh. 4.5 - Prob. 43ECh. 4.5 - Prob. 44ECh. 4.5 - Prob. 45ECh. 4.5 - Prob. 46ECh. 4.5 - Prob. 47ECh. 4.5 - Exercises 4752 present data in the form of tables....Ch. 4.5 - Prob. 49ECh. 4.5 - Prob. 50ECh. 4.5 - Prob. 51ECh. 4.5 - Prob. 52ECh. 4.5 - In Exercises 5356, rewrite the equation in terms...Ch. 4.5 - Prob. 54ECh. 4.5 - Prob. 55ECh. 4.5 - In Exercises 5356, rewrite the equation in terms...Ch. 4.5 - Nigeria has a growth rate of 0.025 or 2.5%....Ch. 4.5 - Prob. 58ECh. 4.5 - Prob. 59ECh. 4.5 - What is the half-life of a substance?Ch. 4.5 - Describe a difference between exponential growth...Ch. 4.5 - Describe the shape of a scatter plot that suggests...Ch. 4.5 - Prob. 63ECh. 4.5 - Would you prefer that your salary be modeled...Ch. 4.5 - Prob. 65ECh. 4.5 - Prob. 66ECh. 4.5 - Prob. 67ECh. 4.5 - In Example 1 on page 520, we used two data points...Ch. 4.5 - Prob. 69ECh. 4.5 - In Example 1 on page 520, we used two data points...Ch. 4.5 - Prob. 71ECh. 4.5 - Prob. 72ECh. 4.5 - Prob. 73ECh. 4.5 - Prob. 74ECh. 4.5 - Make Sense? In Exercises 7376, determine whether...Ch. 4.5 - Make Sense? In Exercises 7376, determine whether...Ch. 4.5 - The exponential growth models describe the...Ch. 4.5 - Prob. 78ECh. 4.5 - Prob. 79ECh. 4.5 - Prob. 80ECh. 4.5 - Prob. 81ECh. 4.5 - Prob. 83ECh. 4.5 - Prob. 84ECh. 4.5 - Prob. 85ECh. 4.5 - Exercises 8688 will help you prepare for the...Ch. 4.5 - Prob. 87ECh. 4.5 - Prob. 88ECh. 4 - In Exercises 1-5, graph f and g in the same...Ch. 4 - In Exercises 1-5, graph f and g in the same...Ch. 4 - In Exercises 1-5, graph f and g in the same...Ch. 4 - Prob. 4MCCh. 4 - Prob. 5MCCh. 4 - Prob. 6MCCh. 4 - Prob. 7MCCh. 4 - Prob. 8MCCh. 4 - Prob. 9MCCh. 4 - Prob. 10MCCh. 4 - Prob. 11MCCh. 4 - Prob. 12MCCh. 4 - In Exercises 10-20, evaluate each expression...Ch. 4 - Prob. 14MCCh. 4 - Prob. 15MCCh. 4 - Prob. 16MCCh. 4 - Prob. 17MCCh. 4 - In Exercises 10-20, evaluate each expression...Ch. 4 - Prob. 19MCCh. 4 - Prob. 20MCCh. 4 - Prob. 21MCCh. 4 - In Exercises 21-22, expand and evaluate numerical...Ch. 4 - Prob. 23MCCh. 4 - Prob. 24MCCh. 4 - Prob. 25MCCh. 4 - Use the formulas A=P(1+rn)nt and A=Pert to solve...Ch. 4 - Prob. 1RECh. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - In Exercises 59, graph f and g in the same...Ch. 4 - Prob. 9RECh. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 - Prob. 14RECh. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - In Exercises 1929, evaluate each expression...Ch. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - In Exercises 1929, evaluate each expression...Ch. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Prob. 33RECh. 4 - Prob. 34RECh. 4 - Prob. 35RECh. 4 - Prob. 36RECh. 4 - Prob. 37RECh. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 40RECh. 4 - Prob. 41RECh. 4 - Prob. 42RECh. 4 - Prob. 43RECh. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - Prob. 47RECh. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - In Exercises 5053, use properties of logarithms to...Ch. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - In Exercises 5859, use common logarithms or...Ch. 4 - In Exercises 5859, use common logarithms or...Ch. 4 - Prob. 60RECh. 4 - Prob. 61RECh. 4 - Prob. 62RECh. 4 - Prob. 63RECh. 4 - Prob. 64RECh. 4 - Prob. 65RECh. 4 - Prob. 66RECh. 4 - Prob. 67RECh. 4 - In Exercises 6473, solve each exponential...Ch. 4 - Prob. 69RECh. 4 - Prob. 70RECh. 4 - Prob. 71RECh. 4 - Prob. 72RECh. 4 - Prob. 73RECh. 4 - Prob. 74RECh. 4 - Prob. 75RECh. 4 - Prob. 76RECh. 4 - In Exercises 74-79, solve each logarithmic...Ch. 4 - Prob. 78RECh. 4 - Prob. 79RECh. 4 - Prob. 80RECh. 4 - Prob. 81RECh. 4 - Prob. 82RECh. 4 - Prob. 83RECh. 4 - Prob. 84RECh. 4 - Prob. 85RECh. 4 - Prob. 86RECh. 4 - Prob. 87RECh. 4 - Prob. 88RECh. 4 - Prob. 89RECh. 4 - Prob. 90RECh. 4 - Prob. 91RECh. 4 - Prob. 92RECh. 4 - Prob. 93RECh. 4 - Prob. 94RECh. 4 - Prob. 1TCh. 4 - Prob. 2TCh. 4 - Prob. 3TCh. 4 - Prob. 4TCh. 4 - Prob. 5TCh. 4 - Prob. 6TCh. 4 - Prob. 7TCh. 4 - Prob. 8TCh. 4 - Prob. 9TCh. 4 - Prob. 10TCh. 4 - Prob. 11TCh. 4 - Prob. 12TCh. 4 - Prob. 13TCh. 4 - Prob. 14TCh. 4 - Prob. 15TCh. 4 - Prob. 16TCh. 4 - Prob. 17TCh. 4 - Prob. 18TCh. 4 - Prob. 19TCh. 4 - Prob. 20TCh. 4 - Prob. 21TCh. 4 - Prob. 22TCh. 4 - Use the compound interest formulas to solve...Ch. 4 - Prob. 24TCh. 4 - Prob. 25TCh. 4 - The function A=82.3e0.004t models the population...Ch. 4 - Prob. 27TCh. 4 - Use the exponential decay model, A = A0ekt, to...Ch. 4 - Prob. 29TCh. 4 - Prob. 30TCh. 4 - Prob. 31TCh. 4 - Prob. 32TCh. 4 - Prob. 33TCh. 4 - Prob. 34TCh. 4 - Prob. 1CURCh. 4 - Prob. 2CURCh. 4 - Prob. 3CURCh. 4 - Prob. 4CURCh. 4 - Prob. 5CURCh. 4 - Prob. 6CURCh. 4 - Prob. 7CURCh. 4 - Prob. 8CURCh. 4 - Prob. 9CURCh. 4 - Prob. 10CURCh. 4 - Prob. 11CURCh. 4 - Prob. 12CURCh. 4 - Prob. 13CURCh. 4 - Prob. 14CURCh. 4 - Prob. 15CURCh. 4 - Prob. 16CURCh. 4 - you discover that the umber of hours you sleep...Ch. 4 - Prob. 18CURCh. 4 - Prob. 19CURCh. 4 - Prob. 20CUR
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Question 4 Find the value of the first element for the first row of the inverse matrix of matrix B. 3 Not yet answered B = Marked out of 5.00 · (³ ;) Flag question 7 [Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places] Answer:arrow_forwardQuestion 2 Not yet answered Multiply the following Matrices together: [77-4 A = 36 Marked out of -5 -5 5.00 B = 3 5 Flag question -6 -7 ABarrow_forwardAssume {u1, U2, u3, u4} does not span R³. Select the best statement. A. {u1, U2, u3} spans R³ if u̸4 is a linear combination of other vectors in the set. B. We do not have sufficient information to determine whether {u₁, u2, u3} spans R³. C. {U1, U2, u3} spans R³ if u̸4 is a scalar multiple of another vector in the set. D. {u1, U2, u3} cannot span R³. E. {U1, U2, u3} spans R³ if u̸4 is the zero vector. F. none of the abovearrow_forward
- Select the best statement. A. If a set of vectors includes the zero vector 0, then the set of vectors can span R^ as long as the other vectors are distinct. n B. If a set of vectors includes the zero vector 0, then the set of vectors spans R precisely when the set with 0 excluded spans Rª. ○ C. If a set of vectors includes the zero vector 0, then the set of vectors can span Rn as long as it contains n vectors. ○ D. If a set of vectors includes the zero vector 0, then there is no reasonable way to determine if the set of vectors spans Rn. E. If a set of vectors includes the zero vector 0, then the set of vectors cannot span Rn. F. none of the abovearrow_forwardWhich of the following sets of vectors are linearly independent? (Check the boxes for linearly independent sets.) ☐ A. { 7 4 3 13 -9 8 -17 7 ☐ B. 0 -8 3 ☐ C. 0 ☐ D. -5 ☐ E. 3 ☐ F. 4 THarrow_forward3 and = 5 3 ---8--8--8 Let = 3 U2 = 1 Select all of the vectors that are in the span of {u₁, u2, u3}. (Check every statement that is correct.) 3 ☐ A. The vector 3 is in the span. -1 3 ☐ B. The vector -5 75°1 is in the span. ГОЛ ☐ C. The vector 0 is in the span. 3 -4 is in the span. OD. The vector 0 3 ☐ E. All vectors in R³ are in the span. 3 F. The vector 9 -4 5 3 is in the span. 0 ☐ G. We cannot tell which vectors are i the span.arrow_forward
- (20 p) 1. Find a particular solution satisfying the given initial conditions for the third-order homogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y(3)+2y"-y-2y = 0; y(0) = 1, y'(0) = 2, y"(0) = 0; y₁ = e*, y2 = e¯x, y3 = e−2x (20 p) 2. Find a particular solution satisfying the given initial conditions for the second-order nonhomogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y"-2y-3y = 6; y(0) = 3, y'(0) = 11 yc = c₁ex + c2e³x; yp = −2 (60 p) 3. Find the general, and if possible, particular solutions of the linear systems of differential equations given below using the eigenvalue-eigenvector method. (See Section 7.3 in your textbook if you need a review of the subject.) = a) x 4x1 + x2, x2 = 6x1-x2 b) x=6x17x2, x2 = x1-2x2 c) x = 9x1+5x2, x2 = −6x1-2x2; x1(0) = 1, x2(0)=0arrow_forwardFind the perimeter and areaarrow_forwardAssume {u1, U2, us} spans R³. Select the best statement. A. {U1, U2, us, u4} spans R³ unless u is the zero vector. B. {U1, U2, us, u4} always spans R³. C. {U1, U2, us, u4} spans R³ unless u is a scalar multiple of another vector in the set. D. We do not have sufficient information to determine if {u₁, u2, 43, 114} spans R³. OE. {U1, U2, 3, 4} never spans R³. F. none of the abovearrow_forward
- Assume {u1, U2, 13, 14} spans R³. Select the best statement. A. {U1, U2, u3} never spans R³ since it is a proper subset of a spanning set. B. {U1, U2, u3} spans R³ unless one of the vectors is the zero vector. C. {u1, U2, us} spans R³ unless one of the vectors is a scalar multiple of another vector in the set. D. {U1, U2, us} always spans R³. E. {U1, U2, u3} may, but does not have to, span R³. F. none of the abovearrow_forwardLet H = span {u, v}. For each of the following sets of vectors determine whether H is a line or a plane. Select an Answer u = 3 1. -10 8-8 -2 ,v= 5 Select an Answer -2 u = 3 4 2. + 9 ,v= 6arrow_forwardSolve for the matrix X: X (2 7³) x + ( 2 ) - (112) 6 14 8arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
What is Ellipse?; Author: Don't Memorise;https://www.youtube.com/watch?v=nzwCInIMlU4;License: Standard YouTube License, CC-BY