Calculus Volume 1
17th Edition
ISBN: 9781938168024
Author: Strang, Gilbert
Publisher: OpenStax College
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 4.1, Problem 41E
You are walking to a bus stop at a right-angle corner. You move north at a rate of 2 m/sec and are 20 m south of the intersection. The bus navels west at a rate of 10 m/ sec away from the intersection - you have missed die bus! What is die rate at which the angle between you and the bus is changing when you are 20 m south of the intersection and the bus is 10 m west of the intersection?
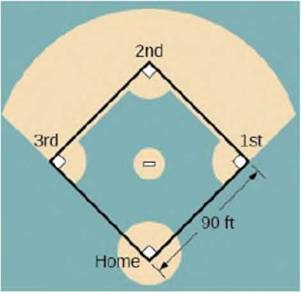
For the following exercises, refer to the figure of baseball diamond, which has sides of 90 ft.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Let’s say you’re on top of a cliff, which drops vertically 150m to the ocean below. You throw a ball with an initial speed of 8.40m/s at an angle of 20 above the horizontal. About how many meters is it from the base of the cliff to the point of impact? Use g=9.806m/s2 for gravity.
A rocket is rising at a constant speed of 5 mi/s. A person is filming from their car on a straight road at a speed of 13/12 mi/s. When the car passes directly under the rocket, the rocket is 3 miles above the car. How fast is the distance between the car and the rocketincreasing 2 seconds later? (Answer: 5.1 mi/s)
The tempature at any point on a cordinate plane is T=3x2+4y2+5.
What is the rate of change from the origin, considering it's the same in any direction? Why is it the same rate of change?
Chapter 4 Solutions
Calculus Volume 1
Ch. 4.1 - For the following exercises, find the quantities...Ch. 4.1 - For the following exercises, find the quantities...Ch. 4.1 - For the following exercises, find the quantities...Ch. 4.1 - For the following exercises, sketch the situation...Ch. 4.1 - For the following exercises, sketch the situation...Ch. 4.1 - A 25-ft ladder is leaning against a wall. If we...Ch. 4.1 - Two airplanes are flying in the air at the same...Ch. 4.1 - You and a friend are riding your bikes to a...Ch. 4.1 - Two buses are driving along parallel freeways that...Ch. 4.1 - A 6-ft-tall person walks away from a 10-ft...
Ch. 4.1 - Using the previous problem, what is the rate at...Ch. 4.1 - A 5-ft-tall person walks toward a wall at a rate...Ch. 4.1 - Using the previous problem, what is the rate at...Ch. 4.1 - A helicopter starting on the ground is rising...Ch. 4.1 - Using the previous problem, what is the rate at...Ch. 4.1 - For the following exercises, draw and label...Ch. 4.1 - For the following exercises, draw and label...Ch. 4.1 - For the following exercises, draw and label...Ch. 4.1 - For the following exercises, draw and label...Ch. 4.1 - For the following exercises, draw and label...Ch. 4.1 - For the following exercises, draw and label...Ch. 4.1 - For the following exercises, draw and label...Ch. 4.1 - For the following exercises, draw and label...Ch. 4.1 - For the following exercises, draw and label...Ch. 4.1 - For the following exercises, consider a tight cone...Ch. 4.1 - For the following exercises, consider a right cone...Ch. 4.1 - For the following exercises, consider a right cone...Ch. 4.1 - For the following exercises, consider a tight cone...Ch. 4.1 - For the following exercises, consider a right cone...Ch. 4.1 - A trough has ends shaped like isosceles triangles,...Ch. 4.1 - A tank is shaped like an upside-down square...Ch. 4.1 - For the following problems, consider a pool shaped...Ch. 4.1 - For the following problems, consider a pool shaped...Ch. 4.1 - For the following problems, consider a pool shaped...Ch. 4.1 - For the following problems, consider a pool shaped...Ch. 4.1 - For the following problems, consider a pool shaped...Ch. 4.1 - For the following exercises, draw the situations...Ch. 4.1 - For the following exercises, draw the situations...Ch. 4.1 - A lighthouse, L, is on an island 4 mi away from...Ch. 4.1 - Using the same setup as the previous problem,...Ch. 4.1 - You are walking to a bus stop at a right-angle...Ch. 4.1 - [T] A batter hits a ball toward third base at 75...Ch. 4.1 - [T] A batter hits a ball toward second base at 80...Ch. 4.1 - [T] A batter hits the ball and runs toward first...Ch. 4.1 - Runners start at first and second base. When the...Ch. 4.2 - What is the linear approximation for any generic...Ch. 4.2 - Determine the necessary conditions such that the...Ch. 4.2 - Explain why the linear approximation becomes less...Ch. 4.2 - When is the linear approximation exact?Ch. 4.2 - For the following exercises, find the linear...Ch. 4.2 - ]For the following exercises, find the linear...Ch. 4.2 - For the following exercises, find the linear...Ch. 4.2 - For the following exercises, find the linear...Ch. 4.2 - For the following exercises, find he linear...Ch. 4.2 - For the following exercises, find the linear...Ch. 4.2 - For the following exercises, compute the values...Ch. 4.2 - For the following exercises, compute the values...Ch. 4.2 - For the following exercises, compute the values...Ch. 4.2 - For the following exercises, compute the values...Ch. 4.2 - For the following exercises, compute the values...Ch. 4.2 - For the following exercises, compute the values...Ch. 4.2 - For the following exercises, determine the...Ch. 4.2 - For the following exercises, determine the...Ch. 4.2 - For the following exercises, determine the...Ch. 4.2 - For the following exercises, determine the...Ch. 4.2 - For the following exercises, determine the...Ch. 4.2 - For the following exercises, determine the...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the differential...Ch. 4.2 - For the following exercises, find the change in...Ch. 4.2 - For the following exercises, find the change in...Ch. 4.2 - For the following exercises, find the change in...Ch. 4.2 - For the following exercises, find the change in...Ch. 4.2 - For the following exercises, find the change in...Ch. 4.2 - For the following exercises, find the change in...Ch. 4.2 - For the following exercises, use differentials to...Ch. 4.2 - For the following exercises, use differentials to...Ch. 4.2 - For the following exercises, use differentials to...Ch. 4.2 - For the following exercises, confirm the...Ch. 4.2 - For the following exercises, confirm the...Ch. 4.2 - For the following exercises, confirm the...Ch. 4.3 - In precalculus, you learned a formula for the...Ch. 4.3 - If you are finding an absolute minimum over an...Ch. 4.3 - If you are examining a function over an interval...Ch. 4.3 - When you are checking for critical points, explain...Ch. 4.3 - Can you have a finite absolute maximum for...Ch. 4.3 - Can you have a finite absolute maximum for...Ch. 4.3 - Let m be the number of local minima and M be the...Ch. 4.3 - Is it possible to have more than one absolute...Ch. 4.3 - Is it possible to have no absolute minimum or...Ch. 4.3 - [T] Graph the function y=eax . For which values of...Ch. 4.3 - For the following exercises, determine where the...Ch. 4.3 - For the following exercises, determine where the...Ch. 4.3 - For the following exercises, determine where the...Ch. 4.3 - For the following exercises, determine where the...Ch. 4.3 - For the following problems, draw graphs of f(x),...Ch. 4.3 - For the following problems, draw graphs of f(x),...Ch. 4.3 - For the following problems, draw graphs of f(x),...Ch. 4.3 - For the following problems, draw graphs of f(x),...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the local and or...Ch. 4.3 - For the following exercises, find the local and/or...Ch. 4.3 - For the following exercises, find the local and/or...Ch. 4.3 - For the following exercises, find the local and or...Ch. 4.3 - For the following exercises, find the local and/or...Ch. 4.3 - For the following exercises, find the local and/or...Ch. 4.3 - For the following exercises, find the local and/or...Ch. 4.3 - For the following exercises, find the local and/or...Ch. 4.3 - For the following exercises, find the local and/or...Ch. 4.3 - For the following exercises, find the local and or...Ch. 4.3 - For the following exercises, find the local and or...Ch. 4.3 - For the following exercises, find the local and...Ch. 4.3 - For the following exercises, find the local and...Ch. 4.3 - For the following exercises, find the local and...Ch. 4.3 - For the following exercises, find the local and...Ch. 4.3 - For the following exercises, find the local and...Ch. 4.3 - For the following exercises, find the local and...Ch. 4.3 - For the following functions, use a calculator to...Ch. 4.3 - For the following functions, use a calculator to...Ch. 4.3 - For the following functions, use a calculator to...Ch. 4.3 - For the following functions, use a calculator to...Ch. 4.3 - For the following functions, use a calculator to...Ch. 4.3 - A company that produces cell phones has a cost...Ch. 4.3 - A ball is thrown into the air and its position is...Ch. 4.3 - For the following exercises, consider the...Ch. 4.3 - For the following exercises, consider the...Ch. 4.3 - Find the critical points, maxima, and minima for...Ch. 4.3 - Find the critical points, maxima, and minima for...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.3 - For the following exercises, find the critical...Ch. 4.4 - Why do you need continuity to apply the Mean Value...Ch. 4.4 - Why do you need differentiability to apply the...Ch. 4.4 - When are Rolle's theorem and the Mean Value...Ch. 4.4 - If you have a function with a discontinuity, is it...Ch. 4.4 - For the following exercises, determine over what...Ch. 4.4 - For the following exercises, determine over what...Ch. 4.4 - For the following exercises, determine over what...Ch. 4.4 - For the following exercises, determine over what...Ch. 4.4 - For the following exercises, determine over what...Ch. 4.4 - For the following exercises, graph the functions...Ch. 4.4 - For the following exercises, graph the functions...Ch. 4.4 - For the following exercises, graph the functions...Ch. 4.4 - For the following exercises, graph the functions...Ch. 4.4 - For the following exercises, use the Mean Value...Ch. 4.4 - For the following exercises, use the Mean Value...Ch. 4.4 - For the following exercises, use the Mean Value...Ch. 4.4 - For the following exercises, use the Mean Value...Ch. 4.4 - For the following exercises, use the Mean Value...Ch. 4.4 - For the following exercises, use the Mean Value...Ch. 4.4 - For the following exercises, show there is no c...Ch. 4.4 - For the following exercises, show there is no c...Ch. 4.4 - For the following exercises, show there is no c...Ch. 4.4 - f(x)=[x](Hint: This is called the floor function...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, determine whether the...Ch. 4.4 - For the following exercises, consider the roots of...Ch. 4.4 - For the following exercises, consider the roots of...Ch. 4.4 - For the following exercises, consider the roots of...Ch. 4.4 - For the following exercises, use a calculator to...Ch. 4.4 - For the following exercises, use a calculator to...Ch. 4.4 - For the following exercises, use a calculator to...Ch. 4.4 - For the following exercises, use a calculator to...Ch. 4.4 - For the following exercises, use a calculator to...Ch. 4.4 - At 10:17 a.m., you pass a police car at 55 mph...Ch. 4.4 - Two cars drive from one spotlight to the next,...Ch. 4.4 - Show that y=sec2x and y=tan2x have the same...Ch. 4.4 - Show that y=csc2x and y=cot2x have the same...Ch. 4.5 - If c is a critical point of f(x), when is there no...Ch. 4.5 - For the function y=x3 , is x=0 both an inflection...Ch. 4.5 - For the function y=x3 , is x=0 an inflection...Ch. 4.5 - Is it possible for a point c to be both an...Ch. 4.5 - Why do you need continuity for the first...Ch. 4.5 - Explain whether a concave-down function has to...Ch. 4.5 - Explain whether a polynomial of degree 2 can have...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, analyze the graphs of...Ch. 4.5 - For the following exercises, draw a graph that...Ch. 4.5 - For the following exercises, draw a graph that...Ch. 4.5 - For the following exercises, draw a graph that...Ch. 4.5 - For the following exercises, draw a graph that...Ch. 4.5 - For the following exercises, draw a graph that...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises. determine a....Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, determine intervals...Ch. 4.5 - For the following exercises, interpret the...Ch. 4.5 - For the following exercises, interpret the...Ch. 4.5 - For the following exercises, interpret the...Ch. 4.5 - For the following exercises, interpret the...Ch. 4.5 - For the following exercises, interpret the...Ch. 4.5 - For the following exercises, consider a...Ch. 4.5 - For the following exercises, consider a...Ch. 4.5 - For the following exercises, consider a...Ch. 4.5 - For the following exercises, consider a...Ch. 4.5 - For the following exercises, consider a...Ch. 4.6 - For the following exercises, examine the graphs....Ch. 4.6 - For the following exercises, examine the graphs....Ch. 4.6 - For the following exercises, examine the graphs....Ch. 4.6 - For the following exercises, examine the graphs....Ch. 4.6 - For the following exercises, examine the graphs....Ch. 4.6 - For the following functions f(x), determine...Ch. 4.6 - For the following functions f(x), determine...Ch. 4.6 - For the following functions f(x), determine...Ch. 4.6 - For the following functions f(x), determine...Ch. 4.6 - For the following functions f(x), determine...Ch. 4.6 - For the following exercises, evaluate the limit....Ch. 4.6 - For the following exercises, evaluate the limit....Ch. 4.6 - For the following exercises, evaluate the limit....Ch. 4.6 - For the following exercises, evaluate the limit....Ch. 4.6 - For the following exercises, evaluate the limit....Ch. 4.6 - For the following exercises, evaluate the limit....Ch. 4.6 - For the following exercises, evaluate the limit....Ch. 4.6 - For the following exercises, evaluate the limit....Ch. 4.6 - For the following exercises, evaluate the limit....Ch. 4.6 - ]For the following exercises, evaluate the limit....Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, find the horizontal...Ch. 4.6 - For the following exercises, graph the function on...Ch. 4.6 - For the following exercises, graph the function on...Ch. 4.6 - For the following exercises, graph the function on...Ch. 4.6 - For the following exercises, graph the function on...Ch. 4.6 - For the following exercises, graph the function on...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For the following exercises, draw a graph of the...Ch. 4.6 - For f(x)=P(x)Q(x) to have an asymptote at y = 2...Ch. 4.6 - For f(x)=P(x)Q(x) to have an asymptote at x = 0...Ch. 4.6 - If f' (x) has asymptotes at y = 3 and x = 1, then...Ch. 4.6 - Both f(x)1x1andg(x)=1( x1)2 have asymptotes at x =...Ch. 4.6 - True or false: Every ratio of polynomials has...Ch. 4.7 - For the following exercises, answer by proof,...Ch. 4.7 - For the following exercises, answer by proof,...Ch. 4.7 - For the following exercises, answer by proof,...Ch. 4.7 - For the following exercises, answer by proof,...Ch. 4.7 - For the following exercises, set up and evaluate...Ch. 4.7 - For the following exercises, set up and evaluate...Ch. 4.7 - For the following exercises, set up and evaluate...Ch. 4.7 - For the following exercises, set up and evaluate...Ch. 4.7 - For the following exercises, consider the...Ch. 4.7 - For the following exercises, consider the...Ch. 4.7 - For the following exercises, consider the...Ch. 4.7 - Two poles are connected by a wire that is also...Ch. 4.7 - You are moving into a new apartment and notice...Ch. 4.7 - A patient’s pulse measures 70 bpm, 80 bpm. then...Ch. 4.7 - In the previous problem, assume the patient was...Ch. 4.7 - You can inn at a speed of 6 mph and swim at a...Ch. 4.7 - Find a function that measures the total amount of...Ch. 4.7 - Find at what angle the lifeguard should swim to...Ch. 4.7 - A truck uses gas as g(v)=av+bv , where v...Ch. 4.7 - Find die cost per mile at speed v.Ch. 4.7 - Find the cheapest driving speed. pizzas for a...Ch. 4.7 - Find the profit function for the number of pizzas...Ch. 4.7 - Assume that R(x)=10x and C(x)=2x+x2 .How many...Ch. 4.7 - Assume that R(x)=15x , and C(x)=60+3x+12x2 . How...Ch. 4.7 - For the following exercises, consider a wire 4 ft...Ch. 4.7 - For the following exercises, consider a wire 4 ft...Ch. 4.7 - For the following exercises, consider two...Ch. 4.7 - For the following exercises, consider two...Ch. 4.7 - For the following exercises, consider two...Ch. 4.7 - For the following exercises, consider two...Ch. 4.7 - For the following exercises, draw the given...Ch. 4.7 - For the following exercises, draw the given...Ch. 4.7 - For the following exercises, draw the given...Ch. 4.7 - For the following exercises, draw the given...Ch. 4.7 - For the following exercises, draw the given...Ch. 4.7 - For the following exercises, draw the given...Ch. 4.7 - For the following exercises, consider the points...Ch. 4.7 - For the following exercises, consider the points...Ch. 4.7 - For the following exercises, consider the points...Ch. 4.7 - For the following exercises, consider the points...Ch. 4.7 - A window is composed of a semicircle placed on top...Ch. 4.7 - You have a garden row of 20 watermelon plants that...Ch. 4.7 - You are constructing a box for your cat to sleep...Ch. 4.7 - You are building five identical pens adjacent to...Ch. 4.7 - You are the manager of an apartment complex with...Ch. 4.8 - For the following exercises, evaluate the limit....Ch. 4.8 - For the following exercises, evaluate the limit....Ch. 4.8 - For the following exercises, evaluate the limit....Ch. 4.8 - For the following exercises, evaluate the limit....Ch. 4.8 - For the following exercises, evaluate the limit....Ch. 4.8 - For the following exercises, evaluate the limit...Ch. 4.8 - For the following exercises, determine whether you...Ch. 4.8 - For the following exercises, determine whether you...Ch. 4.8 - For the following exercises, determine whether you...Ch. 4.8 - For the following exercises, determine whether you...Ch. 4.8 - For the following exercises, determine whether you...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, evaluate the limits...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.8 - For the following exercises, use a calculator to...Ch. 4.9 - Let r = 0.5 and choose x0= 0.2. Either by hand or...Ch. 4.9 - What happens when r =2?Ch. 4.9 - For r = 3.2 and r = 3.5, calculate the first 100...Ch. 4.9 - Now let r = 4. Calculate the first 100 sequence...Ch. 4.9 - Repeat the process for r = 4, but let x0=0.201 ....Ch. 4.9 - For the following exercises, write Newton’s...Ch. 4.9 - For the following exercises, write Newton’s...Ch. 4.9 - For the following exercises, write Newton’s...Ch. 4.9 - For the following exercises, write Newton’s...Ch. 4.9 - For the following exercises, write Newton’s...Ch. 4.9 - For the following exercises, solve f(x) = 0 using...Ch. 4.9 - For the following exercises, solve f(x) = 0 using...Ch. 4.9 - For the following exercises, solve f(x) = 0 using...Ch. 4.9 - For the following exercises, start at x0=0.6and...Ch. 4.9 - For the following exercises, start at x0=0.6and...Ch. 4.9 - For the following exercises, start at x0=0.6and...Ch. 4.9 - For the following exercises, start at x0=0.6and...Ch. 4.9 - For the following exercises, start at x0=0.6and...Ch. 4.9 - For the following exercises, start at x0=0.6and...Ch. 4.9 - For the following exercises, start at x0=0.6and...Ch. 4.9 - For the following exercises, start at x0=0.6and...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, solve to four decimal...Ch. 4.9 - For the following exercises, use Newton’s method...Ch. 4.9 - For the following exercises, use Newton’s method...Ch. 4.9 - For the following exercises, use Newton’s method...Ch. 4.9 - For the following exercises, use Newton’s method...Ch. 4.9 - Newton’s method can be used to find maxima and...Ch. 4.9 - Newton’s method can be used to find maxima and...Ch. 4.9 - Newton’s method can be used to find maxima and...Ch. 4.9 - Newton’s method can be used to find maxima and...Ch. 4.9 - Newton’s method can be used to find maxima and...Ch. 4.9 - Newton’s method can be used to find maxima and...Ch. 4.9 - Newton’s method can be used to find maxima and...Ch. 4.9 - Newton’s method can be used to find maxima and...Ch. 4.9 - Newton’s method can be used to find maxima and...Ch. 4.9 - Minimum of f(x)=x4+x3+3x2+12x+6Ch. 4.9 - For the following exercises, use the specified...Ch. 4.9 - For the following exercises, use the specified...Ch. 4.9 - For the following exercises, use the specified...Ch. 4.9 - For the following exercises, use the specified...Ch. 4.9 - For the following exercises, use the secant...Ch. 4.9 - For the following exercises, use the secant...Ch. 4.9 - For the following exercises, use the secant...Ch. 4.9 - For the following exercises, use the secant...Ch. 4.9 - Why would you use the secant method over Newton's...Ch. 4.9 - For the following exercises, use both Newton’s...Ch. 4.9 - For the following exercises, use both Newton’s...Ch. 4.9 - For the following exercises, use both Newton’s...Ch. 4.9 - For the following exercises, use both Newton’s...Ch. 4.9 - For the following exercises, use both Newton’s...Ch. 4.9 - In the following exercises, consider Kepler's...Ch. 4.9 - In the following exercises, consider Kepler's...Ch. 4.9 - The following two exercises consider a bank...Ch. 4.9 - The fallowing two exercises consider a bank...Ch. 4.9 - The cost for printing a book can be given by the...Ch. 4.10 - For the following exercises, show that F(x) are...Ch. 4.10 - For the following exercises, show that F(x) are...Ch. 4.10 - For the following exercises, show that F(x) are...Ch. 4.10 - For the following exercises, show that F(x) are...Ch. 4.10 - For the following exercises, show that F(x) are...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For die following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, evaluate the...Ch. 4.10 - For the following exercises, evaluate the...Ch. 4.10 - For the following exercises, evaluate the integral...Ch. 4.10 - For the following exercises, evaluate the...Ch. 4.10 - For the following exercises, evaluate the...Ch. 4.10 - For the following exercises, evaluate the...Ch. 4.10 - For the following exercises, evaluate the...Ch. 4.10 - For the following exercises, evaluate the...Ch. 4.10 - For the following exercises, evaluate the...Ch. 4.10 - For the following exercises, solve the initial...Ch. 4.10 - For the following exercises, solve the initial...Ch. 4.10 - For the following exercises, solve the initial...Ch. 4.10 - For the following exercises, solve the initial...Ch. 4.10 - For the following exercises, solve the initial...Ch. 4.10 - For the following exercises, find two possible...Ch. 4.10 - For the following exercises, find two possible...Ch. 4.10 - For the following exercises, find two possible...Ch. 4.10 - For the following exercises, find two possible...Ch. 4.10 - For the following exercises, find two possible...Ch. 4.10 - A car is being driven at a rate of 40 mph when the...Ch. 4.10 - In the preceding problem, calculate how far the...Ch. 4.10 - You are merging onto the freeway, accelerating at...Ch. 4.10 - Based on the previous problem, how far does the...Ch. 4.10 - A car company wants to ensure its newest model can...Ch. 4.10 - A car company wants to ensure its newest model can...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, find the...Ch. 4.10 - For the following exercises, determine whether the...Ch. 4.10 - For the following exercises, determine whether the...Ch. 4.10 - For the following exercises, determine whether the...Ch. 4.10 - For the following exercises, determine whether the...Ch. 4 - True or False? Justify your answer with a proof or...Ch. 4 - True or False? Justify your answer with a proof or...Ch. 4 - True or False? Justify your answer with a proof or...Ch. 4 - True or False? Justify your answer with a proof or...Ch. 4 - Given the graph of f’, determine where f...Ch. 4 - The graph of f is given below. Draw f’.Ch. 4 - Find the linear approximation L(x) to y=x2+tan(x)...Ch. 4 - Find the differential of y=x25x6 and evaluate for...Ch. 4 - Find the critical points and the local and...Ch. 4 - Find the critical points and the local and...Ch. 4 - Determine over which intervals the following...Ch. 4 - Determine over which intervals the following...Ch. 4 - Determine over which intervals the following...Ch. 4 - Determine over which intervals the following...Ch. 4 - Evaluate the following limits. 539. limx3xx2+1x41Ch. 4 - Evaluate the following limits 540. limxcos(1x)Ch. 4 - Evaluate the following limits. 541. limx1x1sin(x)Ch. 4 - Evaluate the following limits. 542. limx(3x)1/xCh. 4 - Use Newton’s method to find the first two...Ch. 4 - Use Newton’s method to find the first two...Ch. 4 - Find the antiderivatives F(x) of the following...Ch. 4 - Find the antiderivatives F(x) of the following...Ch. 4 - Graph the following functions by hand. Make sure...Ch. 4 - Graph the following functions by hand. Make sure...Ch. 4 - A car is being compacted into a rectangular solid....Ch. 4 - A rocket is launched into space; its kinetic...Ch. 4 - The famous Regiomontanus' problem for angle...Ch. 4 - An airline sells tickets from Tokyo to Detroit for...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Use the Information in Example 6.3 to answer the following questions. a. Suppose a 15 to 18-year-old male from ...
Introductory Statistics
The solution of the linear programming problem, Maximize P=x1+2x2+5x3, Subject to x1+3x2+2x3≤60 ...
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
CHECK POINT 1 Write a word description of the set L = {a, b, c, d, e, f}.
Thinking Mathematically (7th Edition)
Use a math drawing to explain in your own words why multiplying the numerator and denominator of a fraction by ...
Mathematics for Elementary Teachers with Activities (5th Edition)
1. To end up with units of speed, you need to
a. multiply a distance by a time.
b. divide a distance by a ti...
Using & Understanding Mathematics: A Quantitative Reasoning Approach (7th Edition)
Of the 1000 first-year students at a certain college, 700 take mathematics courses, 300 take mathematics and ec...
Finite Mathematics & Its Applications (12th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- For the following exercises, find the slope of the lines that pass through each pair of points and determine whether the lines are parallel or perpendicular. 30. F=ma indicates that force (F) equals mass (m)times acceleration (a). Find the acceleration of a mass of 50 kg if a force of 12 N is exerted on it.arrow_forwardA child flies a kite at 90ft. The wind is carrying the kite horizontally away from the child at a rate of 30ft/sec. how fast is the string being paid out when the kite is 150ft away from the child?arrow_forwardPlease give me answer very fast in 5 min nidarrow_forward
- A baseball diamond is a square with side 90 feet. A batter hits the ball and runs toward first base with a speed of 24 ft/s. 90 ft (a) At what rate (in ft/s) is his distance from second base decreasing when he is halfway to first base? (Round your answer to one decimal place.) -8 X ft/s (b) At what rate (in ft/s) is his distance from third base increasing at the same moment? (Round your answer to one decimal place.) 13 X ft/sarrow_forwardDifferentiate r(t) = 5tcos t.arrow_forwardA bright light is sitting on the ground 20 feet from a wall. A 2ft tall dog begins to run from the wall to the bright light at a speed of 3 ft/s. How fast is the dog’s shadow (on the wall) growing when the dog is 15 feet from the wall?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Trigonometric Ratios; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9-eHMMpQC2k;License: Standard YouTube License, CC-BY