PRECALCULUS:...COMMON CORE ED.-W/ACCESS
10th Edition
ISBN: 9780134781839
Author: Demana
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Expert Solution & Answer
Chapter 4.1, Problem 40E
Solution
a.
To identify: The angle in degrees that describe the compass bearing SSE (south southeast)
Refer to the 16 compass bearing shown. North corresponds to an angle of
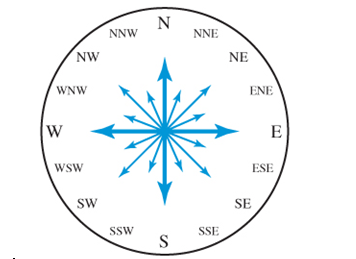
The angle is 202.5 degrees.
Given information:
North corresponds to an angle of
Explanation:
Consider the given information.
SSW represent the 9/16 of the 360-degree compass.
So, the angle is 202.5 degrees.
b.
To identify: The angle in degrees that describe the compass bearing WNW (west north west)
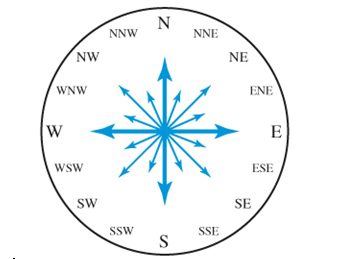
Refer to the 16 compass bearing shown. North corresponds to an angle of
The angle is 292.5 degrees.
Given information:
North corresponds to an angle of
Explanation:
Consider the given information.
WNW represent the 13/16 of the 360-degree compass.
So, the angle is 292.5 degrees.
c.
To identify: The angle in degrees that describe the compass bearing NNW (north north west)
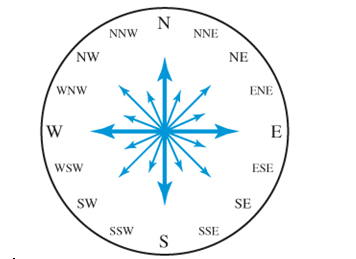
Refer to the 16 compass bearing shown. North corresponds to an angle of
The angle is 337.5 degrees.
Given information:
North corresponds to an angle of
Explanation:
Consider the given information.
NWN represent the 15/16 of the 360-degree compass.
So, the angle is 337.5 degrees.
Chapter 4 Solutions
PRECALCULUS:...COMMON CORE ED.-W/ACCESS
Ch. 4.1 - Prob. 1QRCh. 4.1 - Prob. 2QRCh. 4.1 - Prob. 3QRCh. 4.1 - Prob. 4QRCh. 4.1 - Prob. 5QRCh. 4.1 - Prob. 6QRCh. 4.1 - Prob. 7QRCh. 4.1 - Prob. 8QRCh. 4.1 - Prob. 9QRCh. 4.1 - Prob. 10QR
Ch. 4.1 - Prob. 1ECh. 4.1 - Prob. 2ECh. 4.1 - Prob. 3ECh. 4.1 - Prob. 4ECh. 4.1 - Prob. 5ECh. 4.1 - Prob. 6ECh. 4.1 - Prob. 7ECh. 4.1 - Prob. 8ECh. 4.1 - Prob. 9ECh. 4.1 - Prob. 10ECh. 4.1 - Prob. 11ECh. 4.1 - Prob. 12ECh. 4.1 - Prob. 13ECh. 4.1 - Prob. 14ECh. 4.1 - Prob. 15ECh. 4.1 - Prob. 16ECh. 4.1 - Prob. 17ECh. 4.1 - Prob. 18ECh. 4.1 - Prob. 19ECh. 4.1 - Prob. 20ECh. 4.1 - Prob. 21ECh. 4.1 - Prob. 22ECh. 4.1 - Prob. 23ECh. 4.1 - Prob. 24ECh. 4.1 - Prob. 25ECh. 4.1 - Prob. 26ECh. 4.1 - Prob. 27ECh. 4.1 - Prob. 28ECh. 4.1 - Prob. 29ECh. 4.1 - Prob. 30ECh. 4.1 - Prob. 31ECh. 4.1 - Prob. 32ECh. 4.1 - Prob. 33ECh. 4.1 - Prob. 34ECh. 4.1 - Prob. 35ECh. 4.1 - Prob. 36ECh. 4.1 - Prob. 37ECh. 4.1 - Prob. 38ECh. 4.1 - Prob. 39ECh. 4.1 - Prob. 40ECh. 4.1 - Prob. 41ECh. 4.1 - Prob. 42ECh. 4.1 - Prob. 43ECh. 4.1 - Prob. 44ECh. 4.1 - Prob. 45ECh. 4.1 - Prob. 46ECh. 4.1 - Prob. 47ECh. 4.1 - Prob. 48ECh. 4.1 - Prob. 49ECh. 4.1 - Prob. 50ECh. 4.1 - Prob. 51ECh. 4.1 - Prob. 52ECh. 4.1 - Prob. 53ECh. 4.1 - Prob. 54ECh. 4.1 - Prob. 55ECh. 4.1 - Prob. 56ECh. 4.1 - Prob. 57ECh. 4.1 - Prob. 58ECh. 4.1 - Prob. 59ECh. 4.1 - Prob. 60ECh. 4.1 - Prob. 61ECh. 4.1 - Prob. 62ECh. 4.1 - Prob. 63ECh. 4.1 - Prob. 64ECh. 4.1 - Prob. 65ECh. 4.1 - Prob. 66ECh. 4.1 - Prob. 67ECh. 4.1 - Prob. 68ECh. 4.1 - Prob. 69ECh. 4.1 - Prob. 70ECh. 4.1 - Prob. 71ECh. 4.1 - Prob. 72ECh. 4.1 - Prob. 73ECh. 4.1 - Prob. 74ECh. 4.2 - Prob. 1QRCh. 4.2 - Prob. 2QRCh. 4.2 - Prob. 3QRCh. 4.2 - Prob. 4QRCh. 4.2 - Prob. 5QRCh. 4.2 - Prob. 6QRCh. 4.2 - Prob. 7QRCh. 4.2 - Prob. 8QRCh. 4.2 - Prob. 9QRCh. 4.2 - Prob. 10QRCh. 4.2 - Prob. 1ECh. 4.2 - Prob. 2ECh. 4.2 - Prob. 3ECh. 4.2 - Prob. 4ECh. 4.2 - Prob. 5ECh. 4.2 - Prob. 6ECh. 4.2 - Prob. 7ECh. 4.2 - Prob. 8ECh. 4.2 - Prob. 9ECh. 4.2 - Prob. 10ECh. 4.2 - Prob. 11ECh. 4.2 - Prob. 12ECh. 4.2 - Prob. 13ECh. 4.2 - Prob. 14ECh. 4.2 - Prob. 15ECh. 4.2 - Prob. 16ECh. 4.2 - Prob. 17ECh. 4.2 - Prob. 18ECh. 4.2 - Prob. 19ECh. 4.2 - Prob. 20ECh. 4.2 - Prob. 21ECh. 4.2 - Prob. 22ECh. 4.2 - Prob. 23ECh. 4.2 - Prob. 24ECh. 4.2 - Prob. 25ECh. 4.2 - Prob. 26ECh. 4.2 - Prob. 27ECh. 4.2 - Prob. 28ECh. 4.2 - Prob. 29ECh. 4.2 - Prob. 30ECh. 4.2 - Prob. 31ECh. 4.2 - Prob. 32ECh. 4.2 - Prob. 33ECh. 4.2 - Prob. 34ECh. 4.2 - Prob. 35ECh. 4.2 - Prob. 36ECh. 4.2 - Prob. 37ECh. 4.2 - Prob. 38ECh. 4.2 - Prob. 39ECh. 4.2 - Prob. 40ECh. 4.2 - Prob. 41ECh. 4.2 - Prob. 42ECh. 4.2 - Prob. 43ECh. 4.2 - Prob. 44ECh. 4.2 - Prob. 45ECh. 4.2 - Prob. 46ECh. 4.2 - Prob. 47ECh. 4.2 - Prob. 48ECh. 4.2 - Prob. 49ECh. 4.2 - Prob. 50ECh. 4.2 - Prob. 51ECh. 4.2 - Prob. 52ECh. 4.2 - Prob. 53ECh. 4.2 - Prob. 54ECh. 4.2 - Prob. 55ECh. 4.2 - Prob. 56ECh. 4.2 - Prob. 57ECh. 4.2 - Prob. 58ECh. 4.2 - Prob. 59ECh. 4.2 - Prob. 60ECh. 4.2 - Prob. 61ECh. 4.2 - Prob. 62ECh. 4.2 - Prob. 63ECh. 4.2 - Prob. 64ECh. 4.2 - Prob. 65ECh. 4.2 - Prob. 66ECh. 4.2 - Prob. 67ECh. 4.2 - Prob. 68ECh. 4.2 - Prob. 69ECh. 4.2 - Prob. 70ECh. 4.2 - Prob. 71ECh. 4.2 - Prob. 72ECh. 4.2 - Prob. 73ECh. 4.2 - Prob. 74ECh. 4.2 - Prob. 75ECh. 4.2 - Prob. 76ECh. 4.2 - Prob. 77ECh. 4.2 - Prob. 78ECh. 4.3 - Prob. 1QRCh. 4.3 - Prob. 2QRCh. 4.3 - Prob. 3QRCh. 4.3 - Prob. 4QRCh. 4.3 - Prob. 5QRCh. 4.3 - Prob. 6QRCh. 4.3 - Prob. 7QRCh. 4.3 - Prob. 8QRCh. 4.3 - Prob. 9QRCh. 4.3 - Prob. 10QRCh. 4.3 - Prob. 1ECh. 4.3 - Prob. 2ECh. 4.3 - Prob. 3ECh. 4.3 - Prob. 4ECh. 4.3 - Prob. 5ECh. 4.3 - Prob. 6ECh. 4.3 - Prob. 7ECh. 4.3 - Prob. 8ECh. 4.3 - Prob. 9ECh. 4.3 - Prob. 10ECh. 4.3 - Prob. 11ECh. 4.3 - Prob. 12ECh. 4.3 - Prob. 13ECh. 4.3 - Prob. 14ECh. 4.3 - Prob. 15ECh. 4.3 - Prob. 16ECh. 4.3 - Prob. 17ECh. 4.3 - Prob. 18ECh. 4.3 - Prob. 19ECh. 4.3 - Prob. 20ECh. 4.3 - Prob. 21ECh. 4.3 - Prob. 22ECh. 4.3 - Prob. 23ECh. 4.3 - Prob. 24ECh. 4.3 - Prob. 25ECh. 4.3 - Prob. 26ECh. 4.3 - Prob. 27ECh. 4.3 - Prob. 28ECh. 4.3 - Prob. 29ECh. 4.3 - Prob. 30ECh. 4.3 - Prob. 31ECh. 4.3 - Prob. 32ECh. 4.3 - Prob. 33ECh. 4.3 - Prob. 34ECh. 4.3 - Prob. 35ECh. 4.3 - Prob. 36ECh. 4.3 - Prob. 37ECh. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - Prob. 40ECh. 4.3 - Prob. 41ECh. 4.3 - Prob. 42ECh. 4.3 - Prob. 43ECh. 4.3 - Prob. 44ECh. 4.3 - Prob. 45ECh. 4.3 - Prob. 46ECh. 4.3 - Prob. 47ECh. 4.3 - Prob. 48ECh. 4.3 - Prob. 49ECh. 4.3 - Prob. 50ECh. 4.3 - Prob. 51ECh. 4.3 - Prob. 52ECh. 4.3 - Prob. 53ECh. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Prob. 57ECh. 4.3 - Prob. 58ECh. 4.3 - Prob. 59ECh. 4.3 - Prob. 60ECh. 4.3 - Prob. 61ECh. 4.3 - Prob. 62ECh. 4.3 - Prob. 63ECh. 4.3 - Prob. 64ECh. 4.3 - Prob. 65ECh. 4.3 - Prob. 66ECh. 4.3 - Prob. 67ECh. 4.3 - Prob. 68ECh. 4.3 - Prob. 69ECh. 4.3 - Prob. 70ECh. 4.3 - Prob. 71ECh. 4.3 - Prob. 72ECh. 4.3 - Prob. 73ECh. 4.3 - Prob. 74ECh. 4.3 - Prob. 75ECh. 4.3 - Prob. 76ECh. 4.3 - Prob. 77ECh. 4.3 - Prob. 78ECh. 4.3 - Prob. 79ECh. 4.3 - Prob. 80ECh. 4.4 - Prob. 1QRCh. 4.4 - Prob. 2QRCh. 4.4 - Prob. 3QRCh. 4.4 - Prob. 4QRCh. 4.4 - Prob. 5QRCh. 4.4 - Prob. 6QRCh. 4.4 - Prob. 7QRCh. 4.4 - Prob. 8QRCh. 4.4 - Prob. 9QRCh. 4.4 - Prob. 10QRCh. 4.4 - Prob. 1ECh. 4.4 - Prob. 2ECh. 4.4 - Prob. 3ECh. 4.4 - Prob. 4ECh. 4.4 - Prob. 5ECh. 4.4 - Prob. 6ECh. 4.4 - Prob. 7ECh. 4.4 - Prob. 8ECh. 4.4 - Prob. 9ECh. 4.4 - Prob. 10ECh. 4.4 - Prob. 11ECh. 4.4 - Prob. 12ECh. 4.4 - Prob. 13ECh. 4.4 - Prob. 14ECh. 4.4 - Prob. 15ECh. 4.4 - Prob. 16ECh. 4.4 - Prob. 17ECh. 4.4 - Prob. 18ECh. 4.4 - Prob. 19ECh. 4.4 - Prob. 20ECh. 4.4 - Prob. 21ECh. 4.4 - Prob. 22ECh. 4.4 - Prob. 23ECh. 4.4 - Prob. 24ECh. 4.4 - Prob. 25ECh. 4.4 - Prob. 26ECh. 4.4 - Prob. 27ECh. 4.4 - Prob. 28ECh. 4.4 - Prob. 29ECh. 4.4 - Prob. 30ECh. 4.4 - Prob. 31ECh. 4.4 - Prob. 32ECh. 4.4 - Prob. 33ECh. 4.4 - Prob. 34ECh. 4.4 - Prob. 35ECh. 4.4 - Prob. 36ECh. 4.4 - Prob. 37ECh. 4.4 - Prob. 38ECh. 4.4 - Prob. 39ECh. 4.4 - Prob. 40ECh. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Prob. 43ECh. 4.4 - Prob. 44ECh. 4.4 - Prob. 45ECh. 4.4 - Prob. 46ECh. 4.4 - Prob. 47ECh. 4.4 - Prob. 48ECh. 4.4 - Prob. 49ECh. 4.4 - Prob. 50ECh. 4.4 - Prob. 51ECh. 4.4 - Prob. 52ECh. 4.4 - Prob. 53ECh. 4.4 - Prob. 54ECh. 4.4 - Prob. 55ECh. 4.4 - Prob. 56ECh. 4.4 - Prob. 57ECh. 4.4 - Prob. 58ECh. 4.4 - Prob. 59ECh. 4.4 - Prob. 60ECh. 4.4 - Prob. 61ECh. 4.4 - Prob. 62ECh. 4.4 - Prob. 63ECh. 4.4 - Prob. 64ECh. 4.4 - Prob. 65ECh. 4.4 - Prob. 66ECh. 4.4 - Prob. 67ECh. 4.4 - Prob. 68ECh. 4.4 - Prob. 69ECh. 4.4 - Prob. 70ECh. 4.4 - Prob. 71ECh. 4.4 - Prob. 72ECh. 4.4 - Prob. 73ECh. 4.4 - Prob. 74ECh. 4.4 - Prob. 75ECh. 4.4 - Prob. 76ECh. 4.4 - Prob. 77ECh. 4.4 - Prob. 78ECh. 4.4 - Prob. 79ECh. 4.4 - Prob. 80ECh. 4.4 - Prob. 81ECh. 4.4 - Prob. 82ECh. 4.4 - Prob. 83ECh. 4.4 - Prob. 84ECh. 4.4 - Prob. 85ECh. 4.4 - Prob. 86ECh. 4.4 - Prob. 87ECh. 4.4 - Prob. 88ECh. 4.4 - Prob. 89ECh. 4.4 - Prob. 90ECh. 4.4 - Prob. 91ECh. 4.4 - Prob. 92ECh. 4.4 - Prob. 93ECh. 4.4 - Prob. 94ECh. 4.4 - Prob. 95ECh. 4.4 - Prob. 96ECh. 4.4 - Prob. 97ECh. 4.5 - Prob. 1QRCh. 4.5 - Prob. 2QRCh. 4.5 - Prob. 3QRCh. 4.5 - Prob. 4QRCh. 4.5 - Prob. 5QRCh. 4.5 - Prob. 6QRCh. 4.5 - Prob. 7QRCh. 4.5 - Prob. 8QRCh. 4.5 - Prob. 9QRCh. 4.5 - Prob. 10QRCh. 4.5 - Prob. 1ECh. 4.5 - Prob. 2ECh. 4.5 - Prob. 3ECh. 4.5 - Prob. 4ECh. 4.5 - Prob. 5ECh. 4.5 - Prob. 6ECh. 4.5 - Prob. 7ECh. 4.5 - Prob. 8ECh. 4.5 - Prob. 9ECh. 4.5 - Prob. 10ECh. 4.5 - Prob. 11ECh. 4.5 - Prob. 12ECh. 4.5 - Prob. 13ECh. 4.5 - Prob. 14ECh. 4.5 - Prob. 15ECh. 4.5 - Prob. 16ECh. 4.5 - Prob. 17ECh. 4.5 - Prob. 18ECh. 4.5 - Prob. 19ECh. 4.5 - Prob. 20ECh. 4.5 - Prob. 21ECh. 4.5 - Prob. 22ECh. 4.5 - Prob. 23ECh. 4.5 - Prob. 24ECh. 4.5 - Prob. 25ECh. 4.5 - Prob. 26ECh. 4.5 - Prob. 27ECh. 4.5 - Prob. 28ECh. 4.5 - Prob. 29ECh. 4.5 - Prob. 30ECh. 4.5 - Prob. 31ECh. 4.5 - Prob. 32ECh. 4.5 - Prob. 33ECh. 4.5 - Prob. 34ECh. 4.5 - Prob. 35ECh. 4.5 - Prob. 36ECh. 4.5 - Prob. 37ECh. 4.5 - Prob. 38ECh. 4.5 - Prob. 39ECh. 4.5 - Prob. 40ECh. 4.5 - Prob. 41ECh. 4.5 - Prob. 42ECh. 4.5 - Prob. 43ECh. 4.5 - Prob. 44ECh. 4.5 - Prob. 45ECh. 4.5 - Prob. 46ECh. 4.5 - Prob. 47ECh. 4.5 - Prob. 48ECh. 4.5 - Prob. 49ECh. 4.5 - Prob. 50ECh. 4.5 - Prob. 51ECh. 4.5 - Prob. 52ECh. 4.5 - Prob. 53ECh. 4.5 - Prob. 54ECh. 4.5 - Prob. 55ECh. 4.5 - Prob. 56ECh. 4.5 - Prob. 57ECh. 4.5 - Prob. 58ECh. 4.5 - Prob. 59ECh. 4.5 - Prob. 60ECh. 4.5 - Prob. 61ECh. 4.5 - Prob. 62ECh. 4.5 - Prob. 63ECh. 4.5 - Prob. 64ECh. 4.5 - Prob. 65ECh. 4.5 - Prob. 66ECh. 4.6 - Prob. 1QRCh. 4.6 - Prob. 2QRCh. 4.6 - Prob. 3QRCh. 4.6 - Prob. 4QRCh. 4.6 - Prob. 5QRCh. 4.6 - Prob. 6QRCh. 4.6 - Prob. 7QRCh. 4.6 - Prob. 8QRCh. 4.6 - Prob. 9QRCh. 4.6 - Prob. 10QRCh. 4.6 - Prob. 1ECh. 4.6 - Prob. 2ECh. 4.6 - Prob. 3ECh. 4.6 - Prob. 4ECh. 4.6 - Prob. 5ECh. 4.6 - Prob. 6ECh. 4.6 - Prob. 7ECh. 4.6 - Prob. 8ECh. 4.6 - Prob. 9ECh. 4.6 - Prob. 10ECh. 4.6 - Prob. 11ECh. 4.6 - Prob. 12ECh. 4.6 - Prob. 13ECh. 4.6 - Prob. 14ECh. 4.6 - Prob. 15ECh. 4.6 - Prob. 16ECh. 4.6 - Prob. 17ECh. 4.6 - Prob. 18ECh. 4.6 - Prob. 19ECh. 4.6 - Prob. 20ECh. 4.6 - Prob. 21ECh. 4.6 - Prob. 22ECh. 4.6 - Prob. 23ECh. 4.6 - Prob. 24ECh. 4.6 - Prob. 25ECh. 4.6 - Prob. 26ECh. 4.6 - Prob. 27ECh. 4.6 - Prob. 28ECh. 4.6 - Prob. 29ECh. 4.6 - Prob. 30ECh. 4.6 - Prob. 31ECh. 4.6 - Prob. 32ECh. 4.6 - Prob. 33ECh. 4.6 - Prob. 34ECh. 4.6 - Prob. 35ECh. 4.6 - Prob. 36ECh. 4.6 - Prob. 37ECh. 4.6 - Prob. 38ECh. 4.6 - Prob. 39ECh. 4.6 - Prob. 40ECh. 4.6 - Prob. 41ECh. 4.6 - Prob. 42ECh. 4.6 - Prob. 43ECh. 4.6 - Prob. 44ECh. 4.6 - Prob. 45ECh. 4.6 - Prob. 46ECh. 4.6 - Prob. 47ECh. 4.6 - Prob. 48ECh. 4.6 - Prob. 49ECh. 4.6 - Prob. 50ECh. 4.6 - Prob. 51ECh. 4.6 - Prob. 52ECh. 4.6 - Prob. 53ECh. 4.6 - Prob. 54ECh. 4.6 - Prob. 55ECh. 4.6 - Prob. 56ECh. 4.6 - Prob. 57ECh. 4.6 - Prob. 58ECh. 4.6 - Prob. 59ECh. 4.6 - Prob. 60ECh. 4.6 - Prob. 61ECh. 4.6 - Prob. 62ECh. 4.6 - Prob. 63ECh. 4.6 - Prob. 64ECh. 4.6 - Prob. 65ECh. 4.6 - Prob. 66ECh. 4.6 - Prob. 67ECh. 4.6 - Prob. 68ECh. 4.6 - Prob. 69ECh. 4.6 - Prob. 70ECh. 4.6 - Prob. 71ECh. 4.6 - Prob. 72ECh. 4.6 - Prob. 73ECh. 4.6 - Prob. 74ECh. 4.6 - Prob. 75ECh. 4.6 - Prob. 76ECh. 4.6 - Prob. 77ECh. 4.6 - Prob. 78ECh. 4.6 - Prob. 79ECh. 4.6 - Prob. 80ECh. 4.6 - Prob. 81ECh. 4.6 - Prob. 82ECh. 4.6 - Prob. 83ECh. 4.6 - Prob. 84ECh. 4.6 - Prob. 85ECh. 4.6 - Prob. 86ECh. 4.6 - Prob. 87ECh. 4.6 - Prob. 88ECh. 4.6 - Prob. 89ECh. 4.6 - Prob. 90ECh. 4.6 - Prob. 91ECh. 4.6 - Prob. 92ECh. 4.6 - Prob. 93ECh. 4.6 - Prob. 94ECh. 4.6 - Prob. 95ECh. 4.6 - Prob. 96ECh. 4.7 - Prob. 1QRCh. 4.7 - Prob. 2QRCh. 4.7 - Prob. 3QRCh. 4.7 - Prob. 4QRCh. 4.7 - Prob. 5QRCh. 4.7 - Prob. 6QRCh. 4.7 - Prob. 7QRCh. 4.7 - Prob. 8QRCh. 4.7 - Prob. 9QRCh. 4.7 - Prob. 10QRCh. 4.7 - Prob. 1ECh. 4.7 - Prob. 2ECh. 4.7 - Prob. 3ECh. 4.7 - Prob. 4ECh. 4.7 - Prob. 5ECh. 4.7 - Prob. 6ECh. 4.7 - Prob. 7ECh. 4.7 - Prob. 8ECh. 4.7 - Prob. 9ECh. 4.7 - Prob. 10ECh. 4.7 - Prob. 11ECh. 4.7 - Prob. 12ECh. 4.7 - Prob. 13ECh. 4.7 - Prob. 14ECh. 4.7 - Prob. 15ECh. 4.7 - Prob. 16ECh. 4.7 - Prob. 17ECh. 4.7 - Prob. 18ECh. 4.7 - Prob. 19ECh. 4.7 - Prob. 20ECh. 4.7 - Prob. 21ECh. 4.7 - Prob. 22ECh. 4.7 - Prob. 23ECh. 4.7 - Prob. 24ECh. 4.7 - Prob. 25ECh. 4.7 - Prob. 26ECh. 4.7 - Prob. 27ECh. 4.7 - Prob. 28ECh. 4.7 - Prob. 29ECh. 4.7 - Prob. 30ECh. 4.7 - Prob. 31ECh. 4.7 - Prob. 32ECh. 4.7 - Prob. 33ECh. 4.7 - Prob. 34ECh. 4.7 - Prob. 35ECh. 4.7 - Prob. 36ECh. 4.7 - Prob. 37ECh. 4.7 - Prob. 38ECh. 4.7 - Prob. 39ECh. 4.7 - Prob. 40ECh. 4.7 - Prob. 41ECh. 4.7 - Prob. 42ECh. 4.7 - Prob. 43ECh. 4.7 - Prob. 44ECh. 4.7 - Prob. 45ECh. 4.7 - Prob. 46ECh. 4.7 - Prob. 47ECh. 4.7 - Prob. 48ECh. 4.7 - Prob. 49ECh. 4.7 - Prob. 50ECh. 4.7 - Prob. 51ECh. 4.7 - Prob. 52ECh. 4.7 - Prob. 53ECh. 4.7 - Prob. 54ECh. 4.7 - Prob. 55ECh. 4.7 - Prob. 56ECh. 4.7 - Prob. 57ECh. 4.7 - Prob. 58ECh. 4.7 - Prob. 59ECh. 4.7 - Prob. 60ECh. 4.7 - Prob. 61ECh. 4.7 - Prob. 62ECh. 4.7 - Prob. 63ECh. 4.7 - Prob. 64ECh. 4.7 - Prob. 65ECh. 4.7 - Prob. 66ECh. 4.7 - Prob. 67ECh. 4.7 - Prob. 68ECh. 4.7 - Prob. 69ECh. 4.7 - Prob. 70ECh. 4.7 - Prob. 71ECh. 4.7 - Prob. 72ECh. 4.8 - Prob. 1QRCh. 4.8 - Prob. 2QRCh. 4.8 - Prob. 3QRCh. 4.8 - Prob. 4QRCh. 4.8 - Prob. 5QRCh. 4.8 - Prob. 6QRCh. 4.8 - Prob. 7QRCh. 4.8 - Prob. 8QRCh. 4.8 - Prob. 9QRCh. 4.8 - Prob. 10QRCh. 4.8 - Prob. 1ECh. 4.8 - Prob. 2ECh. 4.8 - Prob. 3ECh. 4.8 - Prob. 4ECh. 4.8 - Prob. 5ECh. 4.8 - Prob. 6ECh. 4.8 - Prob. 7ECh. 4.8 - Prob. 8ECh. 4.8 - Prob. 9ECh. 4.8 - Prob. 10ECh. 4.8 - Prob. 11ECh. 4.8 - Prob. 12ECh. 4.8 - Prob. 13ECh. 4.8 - Prob. 14ECh. 4.8 - Prob. 15ECh. 4.8 - Prob. 16ECh. 4.8 - Prob. 17ECh. 4.8 - Prob. 18ECh. 4.8 - Prob. 19ECh. 4.8 - Prob. 20ECh. 4.8 - Prob. 21ECh. 4.8 - Prob. 22ECh. 4.8 - Prob. 23ECh. 4.8 - Prob. 24ECh. 4.8 - Prob. 25ECh. 4.8 - Prob. 26ECh. 4.8 - Prob. 27ECh. 4.8 - Prob. 28ECh. 4.8 - Prob. 29ECh. 4.8 - Prob. 30ECh. 4.8 - Prob. 31ECh. 4.8 - Prob. 32ECh. 4.8 - Prob. 33ECh. 4.8 - Prob. 34ECh. 4.8 - Prob. 35ECh. 4.8 - Prob. 36ECh. 4.8 - Prob. 37ECh. 4.8 - Prob. 38ECh. 4.8 - Prob. 39ECh. 4.8 - Prob. 40ECh. 4.8 - Prob. 41ECh. 4.8 - Prob. 42ECh. 4.8 - Prob. 43ECh. 4.8 - Prob. 44ECh. 4.8 - Prob. 45ECh. 4.8 - Prob. 46ECh. 4.8 - Prob. 47ECh. 4.8 - Prob. 48ECh. 4.8 - Prob. 49ECh. 4.8 - Prob. 50ECh. 4.8 - Prob. 51ECh. 4 - Prob. 1RECh. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - Prob. 8RECh. 4 - Prob. 9RECh. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 - Prob. 14RECh. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - Prob. 23RECh. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - Prob. 28RECh. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Prob. 33RECh. 4 - Prob. 34RECh. 4 - Prob. 35RECh. 4 - Prob. 36RECh. 4 - Prob. 37RECh. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 40RECh. 4 - Prob. 41RECh. 4 - Prob. 42RECh. 4 - Prob. 43RECh. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - Prob. 47RECh. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - Prob. 50RECh. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - Prob. 58RECh. 4 - Prob. 59RECh. 4 - Prob. 60RECh. 4 - Prob. 61RECh. 4 - Prob. 62RECh. 4 - Prob. 63RECh. 4 - Prob. 64RECh. 4 - Prob. 65RECh. 4 - Prob. 66RECh. 4 - Prob. 67RECh. 4 - Prob. 68RECh. 4 - Prob. 69RECh. 4 - Prob. 70RECh. 4 - Prob. 71RECh. 4 - Prob. 72RECh. 4 - Prob. 73RECh. 4 - Prob. 74RECh. 4 - Prob. 75RECh. 4 - Prob. 76RECh. 4 - Prob. 77RECh. 4 - Prob. 78RECh. 4 - Prob. 79RECh. 4 - Prob. 80RECh. 4 - Prob. 81RECh. 4 - Prob. 82RECh. 4 - Prob. 83RECh. 4 - Prob. 84RECh. 4 - Prob. 85RECh. 4 - Prob. 86RECh. 4 - Prob. 87RECh. 4 - Prob. 88RECh. 4 - Prob. 89RECh. 4 - Prob. 90RECh. 4 - Prob. 91RECh. 4 - Prob. 92RECh. 4 - Prob. 93RECh. 4 - Prob. 94RECh. 4 - Prob. 95RECh. 4 - Prob. 96RECh. 4 - Prob. 97RECh. 4 - Prob. 98RECh. 4 - Prob. 99RECh. 4 - Prob. 100RECh. 4 - Prob. 101RECh. 4 - Prob. 102RECh. 4 - Prob. 103RECh. 4 - Prob. 104RECh. 4 - Prob. 105RECh. 4 - Prob. 106RE
Knowledge Booster
Similar questions
- (10 points) Let f(x, y, z) = ze²²+y². Let E = {(x, y, z) | x² + y² ≤ 4,2 ≤ z ≤ 3}. Calculate the integral f(x, y, z) dv. Earrow_forward(12 points) Let E={(x, y, z)|x²+ y² + z² ≤ 4, x, y, z > 0}. (a) (4 points) Describe the region E using spherical coordinates, that is, find p, 0, and such that (x, y, z) (psin cos 0, psin sin 0, p cos) € E. (b) (8 points) Calculate the integral E xyz dV using spherical coordinates.arrow_forward(10 points) Let f(x, y, z) = ze²²+y². Let E = {(x, y, z) | x² + y² ≤ 4,2 ≤ z < 3}. Calculate the integral y, f(x, y, z) dV.arrow_forward
- (14 points) Let f: R3 R and T: R3. →R³ be defined by f(x, y, z) = ln(x²+ y²+2²), T(p, 0,4)=(psin cos 0, psin sin, pcos). (a) (4 points) Write out the composition g(p, 0, 4) = (foT)(p,, ) explicitly. Then calculate the gradient Vg directly, i.e. without using the chain rule. (b) (4 points) Calculate the gradient Vf(x, y, z) where (x, y, z) = T(p, 0,4). (c) (6 points) Calculate the derivative matrix DT(p, 0, p). Then use the Chain Rule to calculate Vg(r,0,4).arrow_forward(10 points) Let S be the upper hemisphere of the unit sphere x² + y²+2² = 1. Let F(x, y, z) = (x, y, z). Calculate the surface integral J F F-dS. Sarrow_forward(8 points) Calculate the following line integrals. (a) (4 points) F Fds where F(x, y, z) = (x, y, xy) and c(t) = (cost, sint, t), tЄ [0,π] . (b) (4 points) F. Fds where F(x, y, z) = (√xy, e³, xz) where c(t) = (t², t², t), t = [0, 1] .arrow_forward
- review help please and thank you!arrow_forward(10 points) Let S be the surface that is part of the sphere x² + y²+z² = 4 lying below the plane 2√3 and above the plane z-v -√3. Calculate the surface area of S.arrow_forward(8 points) Let D = {(x, y) | 0 ≤ x² + y² ≤4}. Calculate == (x² + y²)³/2dA by making a change of variables to polar coordinates, i.e. x=rcos 0, y = r sin 0.arrow_forward
- x² - y² (10 points) Let f(x,y): = (a) (6 points) For each vector u = (1, 2), calculate the directional derivative Duƒ(1,1). (b) (4 points) Determine all unit vectors u for which Duf(1, 1) = 0.arrow_forwardSolve : X + sin x = 0. By the false positioning numerical methodarrow_forwardSolve: X + sin X = 0 by the false positionining numerical methodarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning