
Represent the maps given in Exercises 37-40 by graphs as we did in Example 6. Recall that we join two vertices by an edge if and only if the states that they represent share a stretch of common border
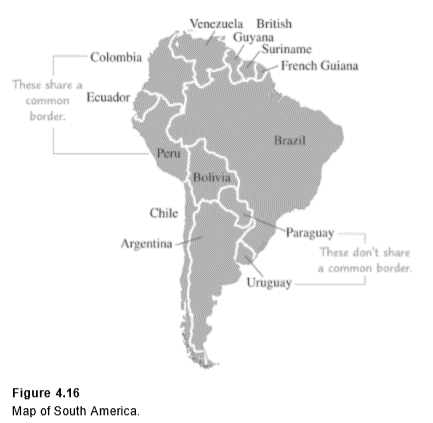
Example 6 Solving the Four-Color Problem for South America
Model the map of South America by a graph and use this graph to color the map using at most four colors.
Solution: In this problem, we have a set of countries, some of which are related in that they share a common border. Therefore, we can model this situation by a graph.
We will represent each country by a vertex; if two countries share a common border, we draw an edge between the corresponding vertices. This graph appears in Figure 4.17 .
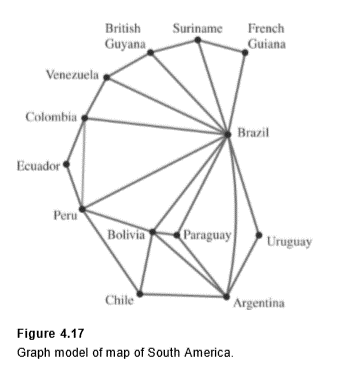
Note that we connect the vertices representing Peru and Colombia with an edge because they share a common boundary. We do not connect the vertices representing Argentina and Peru, because they have no boundary in common.
We can rephrase the map-coloring question now as follows: Using four or fewer colors, can we color the vertices of a graph so that no two vertices of the same edge receive the same color? It is easier to think about coloring a graph than it is to think about coloring the original map.
We show one coloring using four colors in Figure 4.18 and another coloring that I generated on my iPad using a graph theory app called Graphynx. Notice that Graphynx again had to use four colors to color the graph.
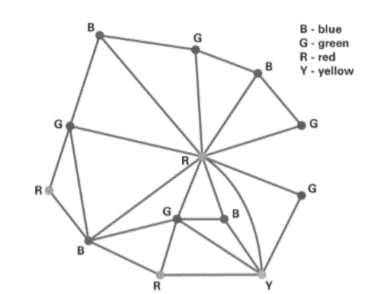
Figure 4.18 Coloring of graph of South America.
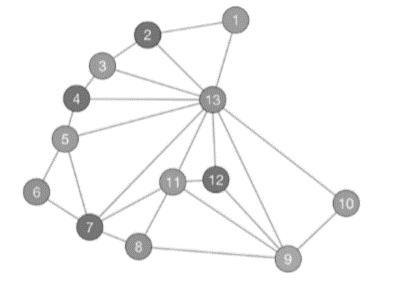
Graphynx coloring of graph of South America.
Want to see the full answer?
Check out a sample textbook solution
Chapter 4 Solutions
Mathematics All Around (6th Edition)
- 5. [10 marks] Determine whether the graph below has a perfect matching. Explain why your answer is correct. ข พarrow_forward(c) Utilize Fubini's Theorem to demonstrate that E(X)= = (1- F(x))dx.arrow_forward(c) Describe the positive and negative parts of a random variable. How is the integral defined for a general random variable using these components?arrow_forward
- Let k ≥ 1, and let G be a k-regular bipartite graph with bipartition X, Y . Prove that |X| is the minimum size of a vertex cover in G.arrow_forward3. [10 marks] Let Go = (V,E) and G₁ = (V,E₁) be two graphs on the same set of vertices. Let (V, EU E1), so that (u, v) is an edge of H if and only if (u, v) is an edge of Go or of G1 (or of both). H = (a) Show that if Go and G₁ are both Eulerian and En E₁ = Ø (i.e., Go and G₁ have no edges in common), then H is also Eulerian. (b) Give an example where Go and G₁ are both Eulerian, but H is not Eulerian.arrow_forward26. (a) Provide an example where X, X but E(X,) does not converge to E(X).arrow_forward
- (b) Demonstrate that if X and Y are independent, then it follows that E(XY) E(X)E(Y);arrow_forward(d) Under what conditions do we say that a random variable X is integrable, specifically when (i) X is a non-negative random variable and (ii) when X is a general random variable?arrow_forward29. State the Borel-Cantelli Lemmas without proof. What is the primary distinction between Lemma 1 and Lemma 2?arrow_forward
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





