
Concept explainers
(a)
The
(a)
Answer to Problem 23P
Solution: The provided values, that is,
Explanation of Solution
Given: The provided table consists of values of x and y, where x represents the average annual hours spent by a person in traffic delay, y represents the average annual gallons of fuel wasted per person due to traffic delay. The data consists of 8 data pairs, thus n is 8.
Calculation: Follow the steps given below in MS Excel to obtain the scatter plot of the data.
Step 1: Enter the data into an MS Excel sheet. The screenshot is given below.
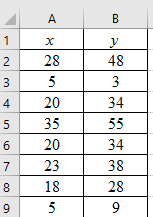
Step 2: Select the data and click on ‘Insert’. Go to charts and select the chart type ‘Scatter’.
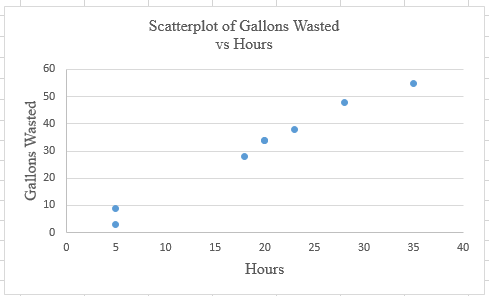
Step 3: Select the first plot and then click ‘add chart element’ provided in the left corner of the menu bar. Insert the ‘Axis titles’ and ‘Chart title’. The scatter plot for the provided data is shown below:
To calculate
| 28 | 48 | 784 | 2304 | 1344 |
| 5 | 3 | 25 | 9 | 15 |
| 20 | 34 | 400 | 1156 | 680 |
| 35 | 55 | 1225 | 3025 | 1925 |
| 20 | 34 | 400 | 1156 | 680 |
| 23 | 38 | 529 | 1444 | 874 |
| 18 | 28 | 324 | 784 | 504 |
| 5 | 9 | 25 | 81 | 45 |
The provided values,
Now, the value of
Substituting the values in the above formula. Thus:
Therefore, the correlation coefficient is 0.991.
(b)
The averages
(b)
Answer to Problem 23P
Solution: The values for data set 1 are
The values for data set 2 are
Explanation of Solution
Given: The provided table consists of values of x and y, where x represents the average annual hours spent by a person in traffic delay, y represents the average annual gallons of fuel wasted per person due to traffic delay.
The second table consists of x and y values where, x represent the annual hours lost by a person spent in traffic delay, y represents the annual gallons of fuel wasted by that person in traffic delay.
The data sets consist of 8 data pairs, thus n is 8 for both the data sets.
The provided values of data set 1 are,
The provided values of data set 2 are,
Calculation:
The value of
The value of
The standard deviation of x for data set 1 can be calculated as,
The standard deviation of
The value of
The value of
The standard deviation of
The standard deviation of
For the second data set, that is, for the variables based on single individuals, the standard deviations
The values
(c)
The scatter plot, whether the provided values of
(c)
Answer to Problem 23P
Solution: The provided values, that is,
Explanation of Solution
The provided table consists of values of x and y, where x represents the average annual hours spent by a person in traffic delay, y represents the average annual gallons of fuel wasted per person due to traffic delay.
The data sets consist of 8 data pairs, thus n is 8.
Calculation: Follow the steps given below in MS Excel to obtain the scatter plot of the data.
Step 1: Enter the data into an MS Excel sheet. The screenshot is given below.
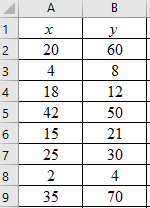
Step 2: Select the data and click on ‘Insert’. Go to charts and select the chart type ‘Scatter’.

Step 3: Select the first plot and then click ‘add chart element’ provided in the left corner of the menu bar. Insert the ‘Axis titles’ and ‘Chart title’. The scatter plot for the provided data is shown below:
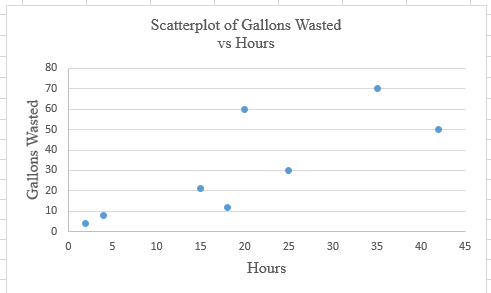
Calculation: The calculation for
| 20 | 60 | 400 | 3600 | 1200 |
| 4 | 8 | 16 | 64 | 32 |
| 18 | 12 | 324 | 144 | 216 |
| 42 | 50 | 1764 | 2500 | 2100 |
| 15 | 21 | 225 | 441 | 315 |
| 25 | 30 | 625 | 900 | 750 |
| 2 | 4 | 4 | 16 | 8 |
| 35 | 70 | 1225 | 4900 | 2450 |
The provided values,
Now, the value of
Substituting the values in the above formula. Thus:
Therefore, the correlation coefficient is 0.794.
(d)
Comparison between the values of r that are calculated in part (a) and part (c), whether the data for average have a higher correlation coefficient than the data for individual measurement or not, and the reason for it.
(d)
Answer to Problem 23P
Solution: Yes, the data for average has a higher correlation coefficient than the data for individual measurement because, according to the central limit theorem, the standard deviation of averages will be smaller than the standard deviation of individual values.
Explanation of Solution
Given: The values of correlation coefficient from part (a) and part (b) are 0.991 and 0.794, respectively.
It can be seen that
According to the central limit theorem, the standard deviation is smaller for the
Want to see more full solutions like this?
Chapter 4 Solutions
UNDERSTANDING BASIC STATISTICS (LOOSE)
- 1. If a firm spends more on advertising, is it likely to increase sales? Data on annual sales (in $100,000s) and advertising expenditures (in $10,000s) were collected for 20 firms in order to estimate the model Sales = Po + B₁Advertising + ε. A portion of the regression results is shown in the accompanying table. Intercept Advertising Standard Coefficients Error t Stat p-value -7.42 1.46 -5.09 7.66E-05 0.42 0.05 8.70 7.26E-08 a. Interpret the estimated slope coefficient. b. What is the sample regression equation? C. Predict the sales for a firm that spends $500,000 annually on advertising.arrow_forwardCan you help me solve problem 38 with steps im stuck.arrow_forwardHow do the samples hold up to the efficiency test? What percentages of the samples pass or fail the test? What would be the likelihood of having the following specific number of efficiency test failures in the next 300 processors tested? 1 failures, 5 failures, 10 failures and 20 failures.arrow_forward
- The battery temperatures are a major concern for us. Can you analyze and describe the sample data? What are the average and median temperatures? How much variability is there in the temperatures? Is there anything that stands out? Our engineers’ assumption is that the temperature data is normally distributed. If that is the case, what would be the likelihood that the Safety Zone temperature will exceed 5.15 degrees? What is the probability that the Safety Zone temperature will be less than 4.65 degrees? What is the actual percentage of samples that exceed 5.25 degrees or are less than 4.75 degrees? Is the manufacturing process producing units with stable Safety Zone temperatures? Can you check if there are any apparent changes in the temperature pattern? Are there any outliers? A closer look at the Z-scores should help you in this regard.arrow_forwardNeed help pleasearrow_forwardPlease conduct a step by step of these statistical tests on separate sheets of Microsoft Excel. If the calculations in Microsoft Excel are incorrect, the null and alternative hypotheses, as well as the conclusions drawn from them, will be meaningless and will not receive any points. 4. One-Way ANOVA: Analyze the customer satisfaction scores across four different product categories to determine if there is a significant difference in means. (Hints: The null can be about maintaining status-quo or no difference among groups) H0 = H1=arrow_forward
- Please conduct a step by step of these statistical tests on separate sheets of Microsoft Excel. If the calculations in Microsoft Excel are incorrect, the null and alternative hypotheses, as well as the conclusions drawn from them, will be meaningless and will not receive any points 2. Two-Sample T-Test: Compare the average sales revenue of two different regions to determine if there is a significant difference. (Hints: The null can be about maintaining status-quo or no difference among groups; if alternative hypothesis is non-directional use the two-tailed p-value from excel file to make a decision about rejecting or not rejecting null) H0 = H1=arrow_forwardPlease conduct a step by step of these statistical tests on separate sheets of Microsoft Excel. If the calculations in Microsoft Excel are incorrect, the null and alternative hypotheses, as well as the conclusions drawn from them, will be meaningless and will not receive any points 3. Paired T-Test: A company implemented a training program to improve employee performance. To evaluate the effectiveness of the program, the company recorded the test scores of 25 employees before and after the training. Determine if the training program is effective in terms of scores of participants before and after the training. (Hints: The null can be about maintaining status-quo or no difference among groups; if alternative hypothesis is non-directional, use the two-tailed p-value from excel file to make a decision about rejecting or not rejecting the null) H0 = H1= Conclusion:arrow_forwardPlease conduct a step by step of these statistical tests on separate sheets of Microsoft Excel. If the calculations in Microsoft Excel are incorrect, the null and alternative hypotheses, as well as the conclusions drawn from them, will be meaningless and will not receive any points. The data for the following questions is provided in Microsoft Excel file on 4 separate sheets. Please conduct these statistical tests on separate sheets of Microsoft Excel. If the calculations in Microsoft Excel are incorrect, the null and alternative hypotheses, as well as the conclusions drawn from them, will be meaningless and will not receive any points. 1. One Sample T-Test: Determine whether the average satisfaction rating of customers for a product is significantly different from a hypothetical mean of 75. (Hints: The null can be about maintaining status-quo or no difference; If your alternative hypothesis is non-directional (e.g., μ≠75), you should use the two-tailed p-value from excel file to…arrow_forward
- Please conduct a step by step of these statistical tests on separate sheets of Microsoft Excel. If the calculations in Microsoft Excel are incorrect, the null and alternative hypotheses, as well as the conclusions drawn from them, will be meaningless and will not receive any points. 1. One Sample T-Test: Determine whether the average satisfaction rating of customers for a product is significantly different from a hypothetical mean of 75. (Hints: The null can be about maintaining status-quo or no difference; If your alternative hypothesis is non-directional (e.g., μ≠75), you should use the two-tailed p-value from excel file to make a decision about rejecting or not rejecting null. If alternative is directional (e.g., μ < 75), you should use the lower-tailed p-value. For alternative hypothesis μ > 75, you should use the upper-tailed p-value.) H0 = H1= Conclusion: The p value from one sample t-test is _______. Since the two-tailed p-value is _______ 2. Two-Sample T-Test:…arrow_forwardPlease conduct a step by step of these statistical tests on separate sheets of Microsoft Excel. If the calculations in Microsoft Excel are incorrect, the null and alternative hypotheses, as well as the conclusions drawn from them, will be meaningless and will not receive any points. What is one sample T-test? Give an example of business application of this test? What is Two-Sample T-Test. Give an example of business application of this test? .What is paired T-test. Give an example of business application of this test? What is one way ANOVA test. Give an example of business application of this test? 1. One Sample T-Test: Determine whether the average satisfaction rating of customers for a product is significantly different from a hypothetical mean of 75. (Hints: The null can be about maintaining status-quo or no difference; If your alternative hypothesis is non-directional (e.g., μ≠75), you should use the two-tailed p-value from excel file to make a decision about rejecting or not…arrow_forwardThe data for the following questions is provided in Microsoft Excel file on 4 separate sheets. Please conduct a step by step of these statistical tests on separate sheets of Microsoft Excel. If the calculations in Microsoft Excel are incorrect, the null and alternative hypotheses, as well as the conclusions drawn from them, will be meaningless and will not receive any points. What is one sample T-test? Give an example of business application of this test? What is Two-Sample T-Test. Give an example of business application of this test? .What is paired T-test. Give an example of business application of this test? What is one way ANOVA test. Give an example of business application of this test? 1. One Sample T-Test: Determine whether the average satisfaction rating of customers for a product is significantly different from a hypothetical mean of 75. (Hints: The null can be about maintaining status-quo or no difference; If your alternative hypothesis is non-directional (e.g., μ≠75), you…arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt


