CALCULUS APPLIED APPROACH >PRINT UGRADE<
10th Edition
ISBN: 9780357667231
Author: Larson
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 4.1, Problem 22E
HOW DO YOU SEE IT? Match the exponential function with its graph. Explain your reasoning. [The graphs are labeled (i), (ii), (in), (iv), (v), and (vi).]
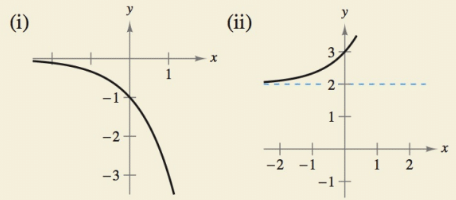
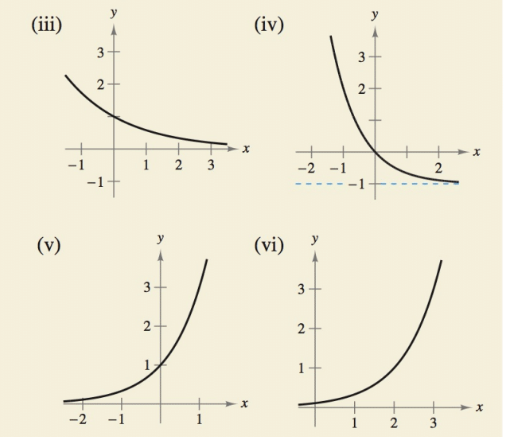
(a)
(b)
(c)
(d)
(e)
(f)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Model the data using an exponential function f(x)
f(x) =
X
0
f(x) 64
1
16
2
4
=
Abx.
What is the exponential function of the graph shown below?
Provide your answer below:
f(x) =
-2.
-2
-5
-6
-8
-9
-10
-11
-12
-13
-14
-15
-16
-17
2.
Model the data using an exponential function f (x) = Ab"
|0 1
2
f(x)
| 500
250
125
O f(x) = 500"
O f (x) = 500(0.5)*
O f (x) = 250(2)"
O f (æ) = 500(2)*
Chapter 4 Solutions
CALCULUS APPLIED APPROACH >PRINT UGRADE<
Ch. 4.1 - Use the properties of exponents to simplify each...Ch. 4.1 - Use the properties of exponents to simplify each...Ch. 4.1 - Use the formula for the ratio of carbon isotopes...Ch. 4.1 - Prob. 4CPCh. 4.1 - Prob. 5CPCh. 4.1 - Prob. 1SWUCh. 4.1 - Prob. 2SWUCh. 4.1 - Prob. 3SWUCh. 4.1 - Prob. 4SWUCh. 4.1 - Prob. 5SWU
Ch. 4.1 - Prob. 6SWUCh. 4.1 - Prob. 7SWUCh. 4.1 - Prob. 8SWUCh. 4.1 - Prob. 9SWUCh. 4.1 - Prob. 10SWUCh. 4.1 - In Exercises 7-12, evaluate each expression....Ch. 4.1 - Prob. 12SWUCh. 4.1 - Prob. 13SWUCh. 4.1 - Prob. 14SWUCh. 4.1 - Prob. 15SWUCh. 4.1 - Prob. 16SWUCh. 4.1 - Prob. 17SWUCh. 4.1 - Prob. 18SWUCh. 4.1 - Applying Properties of Exponents In Exercises 14,...Ch. 4.1 - Prob. 2ECh. 4.1 - Applying Properties of Exponents In Exercises 14,...Ch. 4.1 - Prob. 4ECh. 4.1 - Prob. 5ECh. 4.1 - Prob. 6ECh. 4.1 - Graphing Exponential Functions In Exercises 718,...Ch. 4.1 - Prob. 8ECh. 4.1 - Graphing Exponential Functions In Exercises 7-18,...Ch. 4.1 - Prob. 10ECh. 4.1 - Graphing Exponential Functions In Exercises 7-18,...Ch. 4.1 - Prob. 12ECh. 4.1 - Graphing Exponential Functions In Exercises 7-18,...Ch. 4.1 - Prob. 14ECh. 4.1 - Prob. 15ECh. 4.1 - Prob. 16ECh. 4.1 - Prob. 17ECh. 4.1 - Prob. 18ECh. 4.1 - Population Growth The resident populations P (in...Ch. 4.1 - Sales The sales S (in billions of dollars) for...Ch. 4.1 - Prob. 21ECh. 4.1 - HOW DO YOU SEE IT? Match the exponential function...Ch. 4.1 - Prob. 23ECh. 4.1 - Inflation Rate Repeat Exercise 23 using an annual...Ch. 4.1 - Prob. 25ECh. 4.1 - Drug Concentration Immediately following an...Ch. 4.1 - Prob. 27ECh. 4.2 - Complete the table of values for g(x)=ex. Then...Ch. 4.2 - A bacterial culture is growing according to the...Ch. 4.2 - Find the balance in an account when $2000 is...Ch. 4.2 - Repeat Example 4 using a nominal rate of 7.Ch. 4.2 - Checkpoint 5 Worked-out solution available at...Ch. 4.2 - In Exercises 1-4, discuss the continuity of the...Ch. 4.2 - In Exercises 1-4, discuss the continuity of the...Ch. 4.2 - In Exercises 1-4, discuss the continuity of the...Ch. 4.2 - In Exercises 1-4, discuss the continuity of the...Ch. 4.2 - In Exercises 5-12, find the horizontal asymptote...Ch. 4.2 - In Exercises 5-12, find the horizontal asymptote...Ch. 4.2 - In Exercises 5-12, find the horizontal asymptote...Ch. 4.2 - In Exercises 5-12, find the horizontal asymptote...Ch. 4.2 - In Exercises 5-12, find the horizontal asymptote...Ch. 4.2 - In Exercises 5-12, find the horizontal asymptote...Ch. 4.2 - In Exercises 5-12, find the horizontal asymptote...Ch. 4.2 - In Exercises 5-12, find the horizontal asymptote...Ch. 4.2 - Prob. 1ECh. 4.2 - Applying Properties of Exponents In Exercises 14,...Ch. 4.2 - Applying Properties of Exponents In Exercises 14,...Ch. 4.2 - Applying Properties of Exponents In Exercises 14,...Ch. 4.2 - Matching In Exercises 5-10, match the function...Ch. 4.2 - Matching In Exercises 5-10, match the function...Ch. 4.2 - Matching In Exercises 5-10, match the function...Ch. 4.2 - Matching In Exercises 5-10, match the function...Ch. 4.2 - Matching In Exercises 5-10, match the function...Ch. 4.2 - Matching In Exercises 5-10, match the function...Ch. 4.2 - Graphing Natural Exponential Functions In...Ch. 4.2 - Graphing Natural Exponential Functions In...Ch. 4.2 - Graphing Natural Exponential Functions In...Ch. 4.2 - Graphing Natural Exponential Functions In...Ch. 4.2 - Graphing Natural Exponential Functions In...Ch. 4.2 - Graphing Natural Exponential Functions In...Ch. 4.2 - Graphing Functions In Exercises 1724, use a...Ch. 4.2 - Graphing Functions In Exercises 1724, use a...Ch. 4.2 - Graphing Functions In Exercises 17-24, use a...Ch. 4.2 - Graphing Functions In Exercises 17-24, use a...Ch. 4.2 - Graphing Functions In Exercises 17-24, use a...Ch. 4.2 - Graphing Functions In Exercises 17-24, use a...Ch. 4.2 - Graphing Functions In Exercises 17-24, use a...Ch. 4.2 - Graphing Functions In Exercises 17-24, use a...Ch. 4.2 - Graphing Exponential Functions Use a graphing...Ch. 4.2 - Graphing Logistic Growth Functions Use a graphing...Ch. 4.2 - Finding Present Value In Exercises 31-34, complete...Ch. 4.2 - Finding Present Value In Exercises 31-34, complete...Ch. 4.2 - Finding Present Value In Exercises 31-34, complete...Ch. 4.2 - Finding Present Value In Exercises 31-34, complete...Ch. 4.2 - Finding Present Value In Exercises 31-34, complete...Ch. 4.2 - Finding Present Value In Exercises 31-34, complete...Ch. 4.2 - Finding Present Value In Exercises 31-34, complete...Ch. 4.2 - Finding Present Value In Exercises 3134, complete...Ch. 4.2 - Trust Fund You deposit $15,000 in a trust fund for...Ch. 4.2 - Trust Fund A deposit of $10,000 is made in a trust...Ch. 4.2 - Effective Rate Find the effective rate of interest...Ch. 4.2 - Prob. 38ECh. 4.2 - Present Value How much should be deposited in an...Ch. 4.2 - Present Value How much should be deposited in an...Ch. 4.2 - Demand The demand function for a product is...Ch. 4.2 - Demand The demand function for a product is...Ch. 4.2 - Prob. 43ECh. 4.2 - Consumer Awareness An automobile gets 28 miles per...Ch. 4.2 - Prob. 45ECh. 4.2 - Prob. 46ECh. 4.2 - Prob. 47ECh. 4.2 - Prob. 48ECh. 4.2 - Prob. 49ECh. 4.2 - Learning Theory In a typing class, the average...Ch. 4.2 - Prob. 51ECh. 4.3 - Find the slopes of the tangent lines to the graph...Ch. 4.3 - Differentiate each function. a. f(x)=e3x b....Ch. 4.3 - Prob. 3CPCh. 4.3 - Prob. 4CPCh. 4.3 - The demand function for a product is modeled by...Ch. 4.3 - Graph the normal probability density function...Ch. 4.3 - Prob. 1SWUCh. 4.3 - Prob. 2SWUCh. 4.3 - Prob. 3SWUCh. 4.3 - Prob. 4SWUCh. 4.3 - Prob. 5SWUCh. 4.3 - Prob. 6SWUCh. 4.3 - Prob. 7SWUCh. 4.3 - Prob. 8SWUCh. 4.3 - Prob. 9SWUCh. 4.3 - Prob. 10SWUCh. 4.3 - Differentiating Exponential Functions In Exercises...Ch. 4.3 - Prob. 2ECh. 4.3 - Differentiating Exponential Functions In Exercises...Ch. 4.3 - Prob. 4ECh. 4.3 - Differentiating Exponential Functions In Exercises...Ch. 4.3 - Prob. 6ECh. 4.3 - Differentiating Exponential Functions In Exercises...Ch. 4.3 - Prob. 8ECh. 4.3 - Differentiating Exponential Functions In Exercises...Ch. 4.3 - Prob. 10ECh. 4.3 - Differentiating Exponential Functions In Exercises...Ch. 4.3 - Prob. 12ECh. 4.3 - Differentiating Exponential Functions In Exercises...Ch. 4.3 - Prob. 14ECh. 4.3 - Differentiating Exponential Functions In Exercises...Ch. 4.3 - Prob. 16ECh. 4.3 - Prob. 17ECh. 4.3 - Prob. 18ECh. 4.3 - Prob. 19ECh. 4.3 - Prob. 20ECh. 4.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 4.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 4.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 4.3 - Prob. 24ECh. 4.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 4.3 - Prob. 26ECh. 4.3 - Finding Derivatives Implicitly In Exercises 27-30,...Ch. 4.3 - Prob. 28ECh. 4.3 - Finding Derivatives Implicitly In Exercises 27-30,...Ch. 4.3 - Prob. 30ECh. 4.3 - Finding Second Derivatives In Exercises 31-34,...Ch. 4.3 - Prob. 32ECh. 4.3 - Finding Second Derivatives In Exercises 31-34,...Ch. 4.3 - Prob. 34ECh. 4.3 - Analyzing a Graph In Exercises 35-38, analyze and...Ch. 4.3 - Analyzing a Graph In Exercises 35-38, analyze and...Ch. 4.3 - Prob. 37ECh. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - Prob. 40ECh. 4.3 - Prob. 41ECh. 4.3 - Prob. 42ECh. 4.3 - Catenary A power cable that is suspended between...Ch. 4.3 - Maximum Revenue The demand function for a product...Ch. 4.3 - Depreciation The value V (in dollars) of an item...Ch. 4.3 - Prob. 46ECh. 4.3 - Compound Interest The balance A (in dollars) in a...Ch. 4.3 - Learning Theory The average typing speed N (in...Ch. 4.3 - Prob. 49ECh. 4.3 - Prob. 50ECh. 4.3 - Prob. 51ECh. 4.3 - Prob. 52ECh. 4.3 - Prob. 53ECh. 4.3 - Prob. 1QYCh. 4.3 - Prob. 2QYCh. 4.3 - Prob. 3QYCh. 4.3 - Prob. 4QYCh. 4.3 - Prob. 5QYCh. 4.3 - Prob. 6QYCh. 4.3 - Prob. 7QYCh. 4.3 - Prob. 8QYCh. 4.3 - Prob. 9QYCh. 4.3 - Prob. 10QYCh. 4.3 - Prob. 11QYCh. 4.3 - Prob. 12QYCh. 4.3 - Prob. 13QYCh. 4.3 - Prob. 14QYCh. 4.3 - Prob. 15QYCh. 4.3 - Prob. 16QYCh. 4.3 - Prob. 17QYCh. 4.3 - How much should be deposited in an account paying...Ch. 4.3 - Prob. 19QYCh. 4.3 - Prob. 20QYCh. 4.3 - Prob. 21QYCh. 4.3 - Prob. 22QYCh. 4.3 - Find an equation of the tangent line to the graph...Ch. 4.3 - Prob. 24QYCh. 4.3 - The demand function for a product is modeled by...Ch. 4.4 - Complete the table and sketch the graph of...Ch. 4.4 - Prob. 2CPCh. 4.4 - Prob. 3CPCh. 4.4 - Prob. 4CPCh. 4.4 - Prob. 5CPCh. 4.4 - Prob. 6CPCh. 4.4 - Prob. 7CPCh. 4.4 - Prob. 1SWUCh. 4.4 - Prob. 2SWUCh. 4.4 - Prob. 3SWUCh. 4.4 - Prob. 4SWUCh. 4.4 - Prob. 5SWUCh. 4.4 - Prob. 6SWUCh. 4.4 - Prob. 7SWUCh. 4.4 - Prob. 8SWUCh. 4.4 - Prob. 9SWUCh. 4.4 - Prob. 10SWUCh. 4.4 - Logarithmic and Exponential Forms of Equations In...Ch. 4.4 - Logarithmic and Exponential Forms of Equations In...Ch. 4.4 - Logarithmic and Exponential Forms of Equations In...Ch. 4.4 - Logarithmic and Exponential Forms of Equations In...Ch. 4.4 - Logarithmic and Exponential Forms of Equations In...Ch. 4.4 - Prob. 6ECh. 4.4 - Logarithmic and Exponential Forms of Equations In...Ch. 4.4 - Prob. 8ECh. 4.4 - Prob. 9ECh. 4.4 - Prob. 10ECh. 4.4 - Prob. 11ECh. 4.4 - Prob. 12ECh. 4.4 - Graphing Logarithmic Functions In Exercises 1320,...Ch. 4.4 - Prob. 14ECh. 4.4 - Prob. 15ECh. 4.4 - Prob. 16ECh. 4.4 - Graphing Logarithmic Functions In Exercises 1320,...Ch. 4.4 - Graphing Logarithmic Functions In Exercises 1320,...Ch. 4.4 - Prob. 19ECh. 4.4 - Prob. 20ECh. 4.4 - Applying Inverse Properties In Exercises 2126,...Ch. 4.4 - Prob. 22ECh. 4.4 - Prob. 23ECh. 4.4 - Prob. 24ECh. 4.4 - Applying Inverse Properties In Exercises 2126,...Ch. 4.4 - Prob. 26ECh. 4.4 - Prob. 27ECh. 4.4 - Prob. 28ECh. 4.4 - Expanding Logarithmic Expressions In Exercises...Ch. 4.4 - Prob. 30ECh. 4.4 - Prob. 31ECh. 4.4 - Expanding Logarithmic Expressions In Exercises...Ch. 4.4 - Prob. 33ECh. 4.4 - Prob. 34ECh. 4.4 - Expanding Logarithmic Expressions In Exercises...Ch. 4.4 - Prob. 36ECh. 4.4 - Prob. 37ECh. 4.4 - Prob. 38ECh. 4.4 - Condensing Logarithmic Expressions In Exercises...Ch. 4.4 - Prob. 40ECh. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Condensing Logarithmic Expressions In Exercises...Ch. 4.4 - Prob. 44ECh. 4.4 - Prob. 45ECh. 4.4 - Prob. 46ECh. 4.4 - Solving Exponential and Logarithmic Equations In...Ch. 4.4 - Prob. 48ECh. 4.4 - Solving Exponential and Logarithmic Equations In...Ch. 4.4 - Prob. 50ECh. 4.4 - Prob. 51ECh. 4.4 - Prob. 52ECh. 4.4 - Prob. 53ECh. 4.4 - Prob. 54ECh. 4.4 - Prob. 55ECh. 4.4 - Prob. 56ECh. 4.4 - Solving Exponential and Logarithmic Equations In...Ch. 4.4 - Prob. 58ECh. 4.4 - Prob. 59ECh. 4.4 - Prob. 60ECh. 4.4 - Solving Exponential and Logarithmic Equations In...Ch. 4.4 - Prob. 62ECh. 4.4 - Prob. 63ECh. 4.4 - Prob. 64ECh. 4.4 - Prob. 65ECh. 4.4 - Solving Exponential and Logarithmic Equations In...Ch. 4.4 - Solving Exponential and Logarithmic Equations In...Ch. 4.4 - Prob. 68ECh. 4.4 - Inverse Functions In Exercises 69-72, analytically...Ch. 4.4 - Inverse Functions In Exercises 69-72, analytically...Ch. 4.4 - Prob. 71ECh. 4.4 - Prob. 72ECh. 4.4 - Compound Interest In Exercises 73 and 74, $3000 is...Ch. 4.4 - Compound Interest In Exercises 73 and 74, $3000 is...Ch. 4.4 - Compound Interest A deposit of $1000 is made in an...Ch. 4.4 - Prob. 76ECh. 4.4 - Population Growth The population P (in thousands)...Ch. 4.4 - Population Growth The population P (in thousands)...Ch. 4.4 - Prob. 79ECh. 4.4 - Prob. 80ECh. 4.4 - Prob. 81ECh. 4.4 - Prob. 82ECh. 4.4 - Learning Theory Students in a mathematics class...Ch. 4.4 - HOW DO YOU SEE IT? The graph shows the percents of...Ch. 4.4 - Prob. 85ECh. 4.4 - Prob. 86ECh. 4.4 - Prob. 87ECh. 4.4 - Prob. 88ECh. 4.4 - Prob. 89ECh. 4.4 - Prob. 90ECh. 4.4 - Prob. 91ECh. 4.4 - Prob. 92ECh. 4.4 - Prob. 93ECh. 4.4 - Prob. 94ECh. 4.4 - Prob. 95ECh. 4.4 - Prob. 96ECh. 4.4 - Finance You are investing P dollars at an annual...Ch. 4.4 - Prob. 98ECh. 4.5 - Find the derivative of f(x)=ln5xCh. 4.5 - Prob. 2CPCh. 4.5 - Prob. 3CPCh. 4.5 - Prob. 4CPCh. 4.5 - Prob. 5CPCh. 4.5 - Prob. 6CPCh. 4.5 - Prob. 7CPCh. 4.5 - Prob. 8CPCh. 4.5 - Prob. 9CPCh. 4.5 - Prob. 10CPCh. 4.5 - Prob. 1SWUCh. 4.5 - Prob. 2SWUCh. 4.5 - Prob. 3SWUCh. 4.5 - Prob. 4SWUCh. 4.5 - Prob. 5SWUCh. 4.5 - Prob. 6SWUCh. 4.5 - Prob. 7SWUCh. 4.5 - Prob. 8SWUCh. 4.5 - Prob. 9SWUCh. 4.5 - Prob. 10SWUCh. 4.5 - Differentiating Logarithmic Functions In Exercises...Ch. 4.5 - Prob. 2ECh. 4.5 - Prob. 3ECh. 4.5 - Prob. 4ECh. 4.5 - Differentiating Logarithmic Functions In Exercises...Ch. 4.5 - Prob. 6ECh. 4.5 - Differentiating Logarithmic Functions In Exercises...Ch. 4.5 - Prob. 8ECh. 4.5 - Prob. 9ECh. 4.5 - Prob. 10ECh. 4.5 - Differentiating Logarithmic Functions In Exercises...Ch. 4.5 - Prob. 12ECh. 4.5 - Prob. 13ECh. 4.5 - Prob. 14ECh. 4.5 - Differentiating Logarithmic Functions In Exercises...Ch. 4.5 - Prob. 16ECh. 4.5 - Prob. 17ECh. 4.5 - Prob. 18ECh. 4.5 - Differentiating Logarithmic Functions In Exercises...Ch. 4.5 - Prob. 20ECh. 4.5 - Differentiating Logarithmic Functions In Exercises...Ch. 4.5 - Prob. 22ECh. 4.5 - Prob. 23ECh. 4.5 - Prob. 24ECh. 4.5 - Prob. 25ECh. 4.5 - Evaluating Logarithms In Exercises 23-28, evaluate...Ch. 4.5 - Prob. 27ECh. 4.5 - Prob. 28ECh. 4.5 - Prob. 29ECh. 4.5 - Prob. 30ECh. 4.5 - Prob. 31ECh. 4.5 - Prob. 32ECh. 4.5 - Prob. 33ECh. 4.5 - Prob. 34ECh. 4.5 - Differentiating Functions of Other Bases In...Ch. 4.5 - Prob. 36ECh. 4.5 - Prob. 37ECh. 4.5 - Prob. 38ECh. 4.5 - Prob. 39ECh. 4.5 - Prob. 40ECh. 4.5 - Prob. 41ECh. 4.5 - Prob. 42ECh. 4.5 - Differentiating Functions of Others Bases In...Ch. 4.5 - Differentiating Functions of Others Bases In...Ch. 4.5 - Prob. 45ECh. 4.5 - Prob. 46ECh. 4.5 - Prob. 47ECh. 4.5 - Prob. 48ECh. 4.5 - Finding an Equation of a Tangent Line In Exercises...Ch. 4.5 - Prob. 50ECh. 4.5 - Finding an Equation of a Tangent Line In Exercises...Ch. 4.5 - Prob. 52ECh. 4.5 - Prob. 53ECh. 4.5 - Prob. 54ECh. 4.5 - Prob. 55ECh. 4.5 - Prob. 56ECh. 4.5 - Prob. 57ECh. 4.5 - Prob. 58ECh. 4.5 - Prob. 59ECh. 4.5 - Prob. 60ECh. 4.5 - Prob. 61ECh. 4.5 - Prob. 62ECh. 4.5 - Prob. 63ECh. 4.5 - Chemistry The temperatures T (inF) at which water...Ch. 4.5 - Finding Relative Extrema In Exercises 65-68, find...Ch. 4.5 - Prob. 66ECh. 4.5 - Finding Relative Extrema In Exercises 65-68, find...Ch. 4.5 - Prob. 68ECh. 4.5 - Prob. 69ECh. 4.5 - Prob. 70ECh. 4.5 - Prob. 71ECh. 4.5 - Prob. 72ECh. 4.5 - Demand In Exercises 73 and 74, find dx/dp for the...Ch. 4.5 - Prob. 74ECh. 4.5 - Demand Solve the demand function in Exercise 73...Ch. 4.5 - Demand Solve the demand function in Exercise 74...Ch. 4.5 - Minimum Average Cost The cost of producing x units...Ch. 4.5 - Minimum Average Cost The cost of producing x units...Ch. 4.5 - Prob. 79ECh. 4.5 - HOW DO YOU SEE IT? The graph shows the temperature...Ch. 4.5 - Home Mortgage The term t (in years) of a $200,000...Ch. 4.5 - Prob. 82ECh. 4.5 - Prob. 83ECh. 4.6 - Checkpoint 1 Worked-out solution available at...Ch. 4.6 - Checkpoint 2 Worked-out solution available at...Ch. 4.6 - Checkpoint 3 Worked-out solution available at...Ch. 4.6 - Prob. 4CPCh. 4.6 - Prob. 1SWUCh. 4.6 - Prob. 2SWUCh. 4.6 - Prob. 3SWUCh. 4.6 - Prob. 4SWUCh. 4.6 - Prob. 5SWUCh. 4.6 - Prob. 6SWUCh. 4.6 - Prob. 7SWUCh. 4.6 - Prob. 8SWUCh. 4.6 - In Exercises 9-12, simplify the expression. eln4Ch. 4.6 - Prob. 10SWUCh. 4.6 - Prob. 11SWUCh. 4.6 - Prob. 12SWUCh. 4.6 - Prob. 1ECh. 4.6 - Prob. 2ECh. 4.6 - Modeling Exponential Growth and Decay In Exercises...Ch. 4.6 - Prob. 4ECh. 4.6 - Prob. 5ECh. 4.6 - Prob. 6ECh. 4.6 - Determining Exponential Growth and Decay In...Ch. 4.6 - Determining Exponential Growth and Decay In...Ch. 4.6 - Prob. 9ECh. 4.6 - Determining Exponential Growth and Decay In...Ch. 4.6 - Prob. 11ECh. 4.6 - Prob. 12ECh. 4.6 - Prob. 13ECh. 4.6 - Prob. 14ECh. 4.6 - Prob. 15ECh. 4.6 - Prob. 16ECh. 4.6 - Radioactive Decay What percent of a present amount...Ch. 4.6 - Radioactive Decay Find the half-life of a...Ch. 4.6 - Carbon Dating Carbon-14 (14C) dating assumes that...Ch. 4.6 - Prob. 20ECh. 4.6 - Prob. 21ECh. 4.6 - Prob. 22ECh. 4.6 - Population Growth The number of a certain type of...Ch. 4.6 - Prob. 24ECh. 4.6 - Modeling Compound Interest In Exercises 25-32,...Ch. 4.6 - Prob. 26ECh. 4.6 - Prob. 27ECh. 4.6 - Prob. 28ECh. 4.6 - Prob. 29ECh. 4.6 - Prob. 30ECh. 4.6 - Prob. 31ECh. 4.6 - Prob. 32ECh. 4.6 - Finding Present Value In Exercises 33 and 34,...Ch. 4.6 - Prob. 34ECh. 4.6 - Prob. 35ECh. 4.6 - Prob. 36ECh. 4.6 - Investment: Rule of 70 Verify that the time...Ch. 4.6 - Investment: Rule of 70 Use the Rule of 70 from...Ch. 4.6 - Prob. 39ECh. 4.6 - Population The table shows the populations P (in...Ch. 4.6 - Prob. 41ECh. 4.6 - Sales The cumulative sales S (in thousands of...Ch. 4.6 - Prob. 43ECh. 4.6 - Prob. 44ECh. 4.6 - Revenue A small business assumes that the demand...Ch. 4.6 - Prob. 46ECh. 4 - Applying Properties of Exponents In Exercises 1...Ch. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - Prob. 8RECh. 4 - Prob. 9RECh. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 - Prob. 14RECh. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - Prob. 23RECh. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - Prob. 28RECh. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Biology A lake is stocked with 500 fish, and the...Ch. 4 - Medicine On a college campus of 5000 students, the...Ch. 4 - Prob. 35RECh. 4 - Prob. 36RECh. 4 - Prob. 37RECh. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 40RECh. 4 - Prob. 41RECh. 4 - Prob. 42RECh. 4 - Prob. 43RECh. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - Prob. 47RECh. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - Prob. 50RECh. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - Prob. 58RECh. 4 - Prob. 59RECh. 4 - Prob. 60RECh. 4 - Prob. 61RECh. 4 - Prob. 62RECh. 4 - Prob. 63RECh. 4 - Prob. 64RECh. 4 - Prob. 65RECh. 4 - Prob. 66RECh. 4 - Prob. 67RECh. 4 - Prob. 68RECh. 4 - Prob. 69RECh. 4 - Prob. 70RECh. 4 - Prob. 71RECh. 4 - Prob. 72RECh. 4 - Prob. 73RECh. 4 - Prob. 74RECh. 4 - Prob. 75RECh. 4 - Prob. 76RECh. 4 - Prob. 77RECh. 4 - Prob. 78RECh. 4 - Prob. 79RECh. 4 - Prob. 80RECh. 4 - Prob. 81RECh. 4 - Hourly Earnings The average hourly wages w (in...Ch. 4 - Prob. 83RECh. 4 - Prob. 84RECh. 4 - Prob. 85RECh. 4 - Prob. 86RECh. 4 - Prob. 87RECh. 4 - Prob. 88RECh. 4 - Prob. 89RECh. 4 - Prob. 90RECh. 4 - Prob. 91RECh. 4 - Prob. 92RECh. 4 - Prob. 93RECh. 4 - Prob. 94RECh. 4 - Prob. 95RECh. 4 - Prob. 96RECh. 4 - Prob. 97RECh. 4 - Prob. 98RECh. 4 - Prob. 99RECh. 4 - Prob. 100RECh. 4 - Prob. 101RECh. 4 - Prob. 102RECh. 4 - Prob. 103RECh. 4 - Prob. 104RECh. 4 - Prob. 105RECh. 4 - Prob. 106RECh. 4 - Prob. 107RECh. 4 - Prob. 108RECh. 4 - Prob. 109RECh. 4 - Prob. 110RECh. 4 - Prob. 111RECh. 4 - Prob. 112RECh. 4 - Prob. 113RECh. 4 - Prob. 114RECh. 4 - Prob. 115RECh. 4 - Prob. 116RECh. 4 - Music The numbers of music albums downloaded D (in...Ch. 4 - Minimum Average Cost The cost of producing x units...Ch. 4 - Prob. 119RECh. 4 - Prob. 120RECh. 4 - Prob. 121RECh. 4 - Prob. 122RECh. 4 - Prob. 123RECh. 4 - Prob. 124RECh. 4 - Prob. 125RECh. 4 - Prob. 126RECh. 4 - Prob. 127RECh. 4 - Prob. 128RECh. 4 - Prob. 129RECh. 4 - Prob. 130RECh. 4 - Prob. 131RECh. 4 - Population Growth The number of a certain type of...Ch. 4 - Prob. 1TYSCh. 4 - Prob. 2TYSCh. 4 - Prob. 3TYSCh. 4 - Prob. 4TYSCh. 4 - Prob. 5TYSCh. 4 - Prob. 6TYSCh. 4 - Prob. 7TYSCh. 4 - Prob. 8TYSCh. 4 - Prob. 9TYSCh. 4 - In Exercises 5-10, sketch the graph of the...Ch. 4 - Prob. 11TYSCh. 4 - Prob. 12TYSCh. 4 - Prob. 13TYSCh. 4 - Prob. 14TYSCh. 4 - Prob. 15TYSCh. 4 - Prob. 16TYSCh. 4 - Prob. 17TYSCh. 4 - Prob. 18TYSCh. 4 - Prob. 19TYSCh. 4 - Prob. 20TYSCh. 4 - Prob. 21TYSCh. 4 - Prob. 22TYSCh. 4 - Prob. 23TYSCh. 4 - Prob. 24TYSCh. 4 - Prob. 25TYSCh. 4 - Prob. 26TYSCh. 4 - The sales S (in billions of dollars) of organic...Ch. 4 - Prob. 28TYSCh. 4 - Prob. 29TYS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Which of the following statements is an exponential function? A y=14x+2 (B) y=(6x)² Ⓒ y=(2x+5)3 Dy=2x³(3x² +9)arrow_forwardA deposit of $100 is placed in a savings account. Each month, the amount deposited is doubled. Write the function that models the exponential change between the number of months, t, and the amount of money deposited in the savings account, a(t). O a(t) = 2.100¹ Oa(t) = 100 - 2¹ O a(t) = 100 O a(t)= ()* (1) = 1 1/2 ² 1 · 100¹arrow_forwardMatch the exponential function with one of the graphs labeled I or II. f(x) = 3× + 1 y y 4 3 1 -3 -2 -1 1 2 3 -3 -2 -1 1 3 The graph of f(x) = 3× + 1 is graph I. The graph of f(x) = 3× + 1 is graph II.arrow_forward
- 3 Safin designed and launched an app. One week after he launched the app, it had 8 400 users. Four weeks after he launched the app, it had 23 050 users. The user growth followed the model of an exponential function of the form f(x) = acx, where x: the time elapsed since the app was launched, in weeks f (x): the number of users A company tried to buy Safin's app when it reached 50 000 users. Hoping to make more money, Safin waited and finally sold the app when it reached 400 000 users. To the nearest tenth, how many weeks after the original offer did Safin sell his app?arrow_forward2. A population of bacteria grows exponentially. Initially there was 1500 bacteria. After five hours there was 4500 bacteria. Find a function of time, N (t), which represents the bacteria's population size. (i) Find the population size after ten hours; (ii) Find the time when the population size was 3,000.arrow_forwardThe amount of money in an investment is modeled by the function A(t) = 650(0.7969)'. The variable A represents the investment balance in dollars, and t the number of years since 2001. (A) In 2001, the balance was $ (B) The amount of money in the investment is increasing exponentially (C) The annual rate of change in the balance is r = or r = %. (D) In the year 2009 the investment balance will equal Round answer to the nearest penny. %24arrow_forward
- 1/4.2 Fill in the table of values for each function, then plot your points to graph each curve together on the grid to the right: f(x) = ex f(x) = 4x f(x) = 6* a. x|f(x) = 2x -2 -1 0 b. As the base, b, increases, what happens to the graphs? c. For all of these exponential functions (where b > 1), what's the domain? d. For all of these exponential functions (where b > 1), what's the range? e. For all of these exponential functions (where b > 1), what's the y-intercept? f. For all of these exponential functions (where b > 1), are the graphs increasing or decreasing? g. For all of these exponential functions (where b > 1), is the asymptote vertical or horizontal? h. State the equation of the asymptote:arrow_forwardModel the data using an exponential function f(x) Ab %3D f(x) 125 25 2) 5. 1.arrow_forward2) The value of a plot of land increases 5% every year. The value is $300,000 now, and the owner wants to sell it when the value is at least $400,000. Shanna writes an exponential function of the form, V (t) = a - &, to model the value, V, of the land in t years. The value of b is (A) 1.005 B 1.05 C) 1.5 and the domain is A 0arrow_forwardHow would I solve what f(number inserted) equals?arrow_forwardThe function f(x) = 16(2)x represents the growth of a bee population every year in a remote swamp. Jennifer wants to manipulate the formula to an equivalent form that calculates two times a year, not just once a year. Which function is correct for Jennifer's purpose, and what is the new growth rate? f(x) = 16(2)x; growth rate 200% f(x) = 16(2)2x; growth rate 8% f(x) = 16(1.41)x; growth rate 8% f(x) = 16(1.41)2x; growth rate 41%arrow_forwardarrow_back_iosarrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY