
Numerical Analysis
10th Edition
ISBN: 9781305253667
Author: Richard L. Burden, J. Douglas Faires, Annette M. Burden
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 4.1, Problem 1ES
Use the forward-difference formulas and backward-difference formulas to determine each missing entry in the following tables.
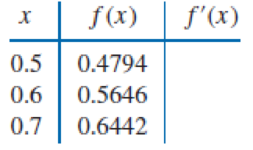
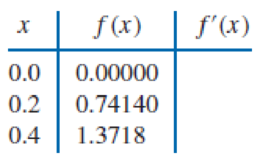
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Remix
4. Direction Fields/Phase Portraits. Use the given direction fields to plot solution curves
to each of the given initial value problems.
(a)
x = x+2y
1111
y = -3x+y
with x(0) = 1, y(0) = -1
(b) Consider the initial value problem corresponding to the given phase portrait.
x = y
y' = 3x + 2y
Draw two "straight line solutions"
passing through (0,0)
(c) Make guesses for the equations of the straight line solutions: y = ax.
It was homework
No chatgpt pls will upvote
Chapter 4 Solutions
Numerical Analysis
Ch. 4.1 - Use the forward-difference formulas and...Ch. 4.1 - The data in Exercise 1 were taken from the...Ch. 4.1 - Use the most accurate three-point formula to...Ch. 4.1 - Use the most accurate three-point formula to...Ch. 4.1 - The data in Exercise 5 were taken from the...Ch. 4.1 - The data in Exercise 6 were taken from the...Ch. 4.1 - Prob. 9ESCh. 4.1 - Use the formulas given in this section to...Ch. 4.1 - The data in Exercise 9 were taken from the...Ch. 4.1 - Prob. 12ES
Ch. 4.1 - Use the following data and the knowledge that the...Ch. 4.1 - Prob. 14ESCh. 4.1 - Prob. 15ESCh. 4.1 - Prob. 16ESCh. 4.1 - Prob. 17ESCh. 4.1 - Prob. 18ESCh. 4.1 - Prob. 19ESCh. 4.1 - Prob. 20ESCh. 4.1 - Prob. 21ESCh. 4.1 - In a circuit with impressed voltage (t) and...Ch. 4.1 - In Exercise 9 of Section 3.4, data were given...Ch. 4.1 - Derive an O(h4) five-point formula to approximate...Ch. 4.1 - Use the formula derived in Exercise 24 and the...Ch. 4.1 - a. Analyze the round-off errors, as in Example 4,...Ch. 4.1 - Derive a method for approximating f (x0) whose...Ch. 4.1 - Consider the function e(h)=h+h26M, where M is a...Ch. 4.1 - Prob. 1DQCh. 4.1 - Prob. 2DQCh. 4.2 - Apply the extrapolation process described in...Ch. 4.2 - Add another line to the extrapolation table in...Ch. 4.2 - The following data give approximations to the...Ch. 4.2 - Prob. 6ESCh. 4.2 - Prob. 7ESCh. 4.2 - The forward-difference formula can be expressed as...Ch. 4.2 - Prob. 9ESCh. 4.2 - Prob. 10ESCh. 4.2 - Prob. 11ESCh. 4.2 - Prob. 12ESCh. 4.2 - Prob. 13ESCh. 4.3 - Approximate the following integrals using the...Ch. 4.3 - Approximate the following integrals using the...Ch. 4.3 - Find a bound for the error in Exercise 1 using the...Ch. 4.3 - Prob. 4ESCh. 4.3 - Repeat Exercise 1 using Simpsons rule. 1....Ch. 4.3 - Prob. 6ESCh. 4.3 - Prob. 7ESCh. 4.3 - Prob. 8ESCh. 4.3 - Prob. 9ESCh. 4.3 - Prob. 10ESCh. 4.3 - Prob. 11ESCh. 4.3 - Prob. 12ESCh. 4.3 - The Trapezoidal rule applied to 02f(x)dx gives the...Ch. 4.3 - Prob. 14ESCh. 4.3 - Approximate the following integrals using formulas...Ch. 4.3 - Prob. 17ESCh. 4.3 - Suppose that the data of Exercise 17 have...Ch. 4.3 - Prob. 19ESCh. 4.3 - Prob. 20ESCh. 4.3 - The quadrature formula...Ch. 4.3 - The quadrature formula...Ch. 4.3 - Find the constants c0, c1, and x1 so that the...Ch. 4.3 - Find the constants x0, x1, and c1 so that the...Ch. 4.3 - Prob. 25ESCh. 4.3 - Prob. 26ESCh. 4.3 - Prob. 27ESCh. 4.3 - Derive Simpsons Three-Eighths rule (the closed...Ch. 4.3 - Prob. 1DQCh. 4.3 - Prob. 2DQCh. 4.4 - Use the Composite Trapezoidal rule with the...Ch. 4.4 - Prob. 2ESCh. 4.4 - Use the Composite Simpsons rule to approximate the...Ch. 4.4 - Prob. 4ESCh. 4.4 - Prob. 5ESCh. 4.4 - Prob. 6ESCh. 4.4 - Prob. 7ESCh. 4.4 - Prob. 8ESCh. 4.4 - Prob. 9ESCh. 4.4 - Prob. 10ESCh. 4.4 - Determine the values of n and h required to...Ch. 4.4 - Repeat Exercise 11 for the integral 0x2cosxdx. 11....Ch. 4.4 - Determine the values of n and h required to...Ch. 4.4 - Repeat Exercise 13 for the integral 12xlnxdx. 13....Ch. 4.4 - Prob. 15ESCh. 4.4 - Prob. 17ESCh. 4.4 - A car laps a race track in 84 seconds. The speed...Ch. 4.4 - Prob. 19ESCh. 4.4 - Prob. 20ESCh. 4.4 - Prob. 21ESCh. 4.4 - Prob. 23ESCh. 4.4 - Prob. 24ESCh. 4.4 - Prob. 25ESCh. 4.4 - Prob. 26ESCh. 4.4 - Prob. 1DQCh. 4.4 - Prob. 2DQCh. 4.5 - Use Romberg integration to compute R3, 3 for the...Ch. 4.5 - Use Romberg integration to compute R3, 3 for the...Ch. 4.5 - Prob. 3ESCh. 4.5 - Prob. 4ESCh. 4.5 - Use the following data to approximate 15f(x)dx as...Ch. 4.5 - Prob. 9ESCh. 4.5 - Prob. 10ESCh. 4.5 - Prob. 11ESCh. 4.5 - Romberg integration for approximating 01f(x)dx...Ch. 4.5 - Prob. 15ESCh. 4.5 - Prob. 18ESCh. 4.5 - Prob. 19ESCh. 4.5 - Prob. 1DQCh. 4.5 - Prob. 4DQCh. 4.6 - Prob. 1ESCh. 4.6 - Prob. 2ESCh. 4.6 - Prob. 11ESCh. 4.6 - Prob. 12ESCh. 4.6 - Could Romberg integration replace Simpsons rule in...Ch. 4.7 - Approximate the following integrals using Gaussian...Ch. 4.7 - Approximate the following integrals using Gaussian...Ch. 4.7 - Repeat Exercise 1 with n = 3. 1. Approximate the...Ch. 4.7 - Repeat Exercise 2 with n = 3. 2. Approximate the...Ch. 4.7 - Repeat Exercise 1 with n = 4. 1. Approximate the...Ch. 4.7 - Repeat Exercise 2 with n = 4. 2. Approximate the...Ch. 4.7 - Repeat Exercise 1 with n = 5. 1. Approximate the...Ch. 4.7 - Repeat Exercise 2 with n = 5. 2. Approximate the...Ch. 4.7 - Describe the differences and similarities between...Ch. 4.7 - Prob. 2DQCh. 4.8 - Prob. 1DQCh. 4.8 - Prob. 2DQCh. 4.8 - Prob. 3DQCh. 4.8 - Prob. 4DQCh. 4.9 - Suppose a body of mass m is traveling vertically...Ch. 4.9 - The Laguerre polynomials {L0(x), L1(x) ...} form...Ch. 4.9 - Prob. 7ESCh. 4.9 - Prob. 8ESCh. 4.9 - Prob. 9ESCh. 4.9 - Prob. 1DQCh. 4.9 - Prob. 2DQ
Additional Math Textbook Solutions
Find more solutions based on key concepts
Length of a Guy Wire A communications tower is located at the top of a steep hill, as shown. The angle of incli...
Precalculus: Mathematics for Calculus (Standalone Book)
Let F be a continuous distribution function. If U is uniformly distributed on (0,1), find the distribution func...
A First Course in Probability (10th Edition)
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
1. How is a sample related to a population?
Elementary Statistics: Picturing the World (7th Edition)
Teacher Salaries
The following data from several years ago represent salaries (in dollars) from a school distri...
Elementary Statistics: A Step By Step Approach
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- (7) (12 points) Let F(x, y, z) = (y, x+z cos yz, y cos yz). Ꮖ (a) (4 points) Show that V x F = 0. (b) (4 points) Find a potential f for the vector field F. (c) (4 points) Let S be a surface in R3 for which the Stokes' Theorem is valid. Use Stokes' Theorem to calculate the line integral Jos F.ds; as denotes the boundary of S. Explain your answer.arrow_forward(3) (16 points) Consider z = uv, u = x+y, v=x-y. (a) (4 points) Express z in the form z = fog where g: R² R² and f: R² → R. (b) (4 points) Use the chain rule to calculate Vz = (2, 2). Show all intermediate steps otherwise no credit. (c) (4 points) Let S be the surface parametrized by T(x, y) = (x, y, ƒ (g(x, y)) (x, y) = R². Give a parametric description of the tangent plane to S at the point p = T(x, y). (d) (4 points) Calculate the second Taylor polynomial Q(x, y) (i.e. the quadratic approximation) of F = (fog) at a point (a, b). Verify that Q(x,y) F(a+x,b+y). =arrow_forward(6) (8 points) Change the order of integration and evaluate (z +4ry)drdy . So S√ ² 0arrow_forward
- (10) (16 points) Let R>0. Consider the truncated sphere S given as x² + y² + (z = √15R)² = R², z ≥0. where F(x, y, z) = −yi + xj . (a) (8 points) Consider the vector field V (x, y, z) = (▼ × F)(x, y, z) Think of S as a hot-air balloon where the vector field V is the velocity vector field measuring the hot gasses escaping through the porous surface S. The flux of V across S gives the volume flow rate of the gasses through S. Calculate this flux. Hint: Parametrize the boundary OS. Then use Stokes' Theorem. (b) (8 points) Calculate the surface area of the balloon. To calculate the surface area, do the following: Translate the balloon surface S by the vector (-15)k. The translated surface, call it S+ is part of the sphere x² + y²+z² = R². Why do S and S+ have the same area? ⚫ Calculate the area of S+. What is the natural spherical parametrization of S+?arrow_forward(1) (8 points) Let c(t) = (et, et sint, et cost). Reparametrize c as a unit speed curve starting from the point (1,0,1).arrow_forward(9) (16 points) Let F(x, y, z) = (x² + y − 4)i + 3xyj + (2x2 +z²)k = - = (x²+y4,3xy, 2x2 + 2²). (a) (4 points) Calculate the divergence and curl of F. (b) (6 points) Find the flux of V x F across the surface S given by x² + y²+2² = 16, z ≥ 0. (c) (6 points) Find the flux of F across the boundary of the unit cube E = [0,1] × [0,1] x [0,1].arrow_forward
- (8) (12 points) (a) (8 points) Let C be the circle x² + y² = 4. Let F(x, y) = (2y + e²)i + (x + sin(y²))j. Evaluate the line integral JF. F.ds. Hint: First calculate V x F. (b) (4 points) Let S be the surface r² + y² + z² = 4, z ≤0. Calculate the flux integral √(V × F) F).dS. Justify your answer.arrow_forwardDetermine whether the Law of Sines or the Law of Cosines can be used to find another measure of the triangle. a = 13, b = 15, C = 68° Law of Sines Law of Cosines Then solve the triangle. (Round your answers to four decimal places.) C = 15.7449 A = 49.9288 B = 62.0712 × Need Help? Read It Watch Itarrow_forward(4) (10 points) Evaluate √(x² + y² + z²)¹⁄² exp[}(x² + y² + z²)²] dV where D is the region defined by 1< x² + y²+ z² ≤4 and √√3(x² + y²) ≤ z. Note: exp(x² + y²+ 2²)²] means el (x²+ y²+=²)²]¸arrow_forward
- (2) (12 points) Let f(x,y) = x²e¯. (a) (4 points) Calculate Vf. (b) (4 points) Given x directional derivative 0, find the line of vectors u = D₁f(x, y) = 0. (u1, 2) such that the - (c) (4 points) Let u= (1+3√3). Show that Duƒ(1, 0) = ¦|▼ƒ(1,0)| . What is the angle between Vf(1,0) and the vector u? Explain.arrow_forwardFind the missing values by solving the parallelogram shown in the figure. (The lengths of the diagonals are given by c and d. Round your answers to two decimal places.) a b 29 39 66.50 C 17.40 d 0 54.0 126° a Ꮎ b darrow_forwardAnswer the following questions related to the following matrix A = 3 ³).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY
Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY
Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY