
(a)
Plot of wave function as a function of
(a)
Answer to Problem 46CP
The wave function was plotted as a function of
Explanation of Solution
Write the given wave function of the electron.
Here,
Write the formula to calculate the probability of finding a particle in a certain range.
Here,
Refer equation (I) and plot the wave function as a function of
Figure 1 below shows the plot of wave function.
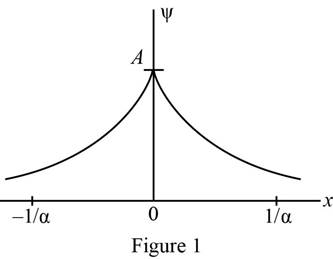
Conclusion:
The wave function was plotted as a function of
(b)
Plot of probability density as a function of
(b)
Answer to Problem 46CP
The probability density was plotted as a function of
Explanation of Solution
Write the given wave function of the electron.
Here,
Write the formula to calculate the probability of finding a particle in a certain range.
Here,
Refer equation (II) and plot the probability density as a function of
Figure 2 below shows the plot of wave function.
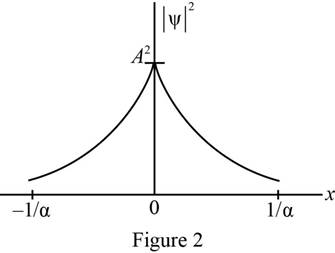
Conclusion:
The probability density was plotted as a function of
(c)
To show that
(c)
Answer to Problem 46CP
The
Explanation of Solution
Write the given wave function of the electron.
Here,
For the wave function to be a reasonable wave function, there are set of condition.
The
As
The
The
Conclusion:
The
(d)
To normalize the wave function.
(d)
Answer to Problem 46CP
The normalization constant of the given wave function is
Explanation of Solution
Write the given wave function of the electron.
Here,
Write the condition for normalized wave function.
The wave function is symmetric. Thus re-write the above condition.
Substitute equation (I) in the above equation.
Conclusion:
The normalization constant of the given wave function is
(e)
The probability of finding the electron in the range
(e)
Answer to Problem 46CP
The probability of finding the particle in the range
Explanation of Solution
Refer section (d) and write the given normalized wave function of the electron.
Here,
Write the formula to calculate the probability of finding a particle in a certain range.
Here,
Refer equation (II) in equation (III) to determine probability in range
Conclusion:
The probability of finding the particle in the range
Want to see more full solutions like this?
Chapter 40 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Multi-term
- The Fiero, which is 4.70 m long, starts at 10.0˚C while in the upper atmosphere but when it goes into space the temperature would be about -270.3˚C. How much should the steel siding of the Fiero shrink due to this temperature change? The coefficient of thermal linear expansion for steel is 11.0⋅10−6⋅10^-6 C-1arrow_forwardQuestion 3 of 17 L X L L T 0.5/ In the figure above, three uniform thin rods, each of length L, form an inverted U. The vertical rods each have a mass m; the horizontal rod has a mass 3m. NOTE: Express your answer in terms of the variables given. (a) What is the x coordinate of the system's center of mass? xcom L 2 (b) What is the y coordinate of the system's center of mass? Ycom 45 L X Q Search MD bp Narrow_forwardSketch the harmonic on graphing paper.arrow_forward
- Exercise 1: (a) Using the explicit formulae derived in the lectures for the (2j+1) × (2j + 1) repre- sentation matrices Dm'm, (J/h), derive the 3 × 3 matrices corresponding to the case j = 1. (b) Verify that they satisfy the so(3) Lie algebra commutation relation: [D(Î₁/ħ), D(Î₂/h)]m'm₁ = iƊm'm² (Ĵ3/h). (c) Prove the identity 3 Dm'm,(β) = Σ (D(Ρ)D(Ρ))m'¡m; · i=1arrow_forwardSketch the harmonic.arrow_forwardFor number 11 please sketch the harmonic on graphing paper.arrow_forward
- # E 94 20 13. Time a) What is the frequency of the above wave? b) What is the period? c) Highlight the second cycle d) Sketch the sine wave of the second harmonic of this wave % 7 & 5 6 7 8 * ∞ Y U 9 0 0 P 150arrow_forwardShow work using graphing paperarrow_forwardCan someone help me answer this physics 2 questions. Thank you.arrow_forward
- Four capacitors are connected as shown in the figure below. (Let C = 12.0 μF.) a C 3.00 με Hh. 6.00 με 20.0 με HE (a) Find the equivalent capacitance between points a and b. 5.92 HF (b) Calculate the charge on each capacitor, taking AV ab = 16.0 V. 20.0 uF capacitor 94.7 6.00 uF capacitor 67.6 32.14 3.00 µF capacitor capacitor C ☑ με με The 3 µF and 12.0 uF capacitors are in series and that combination is in parallel with the 6 μF capacitor. What quantity is the same for capacitors in parallel? μC 32.14 ☑ You are correct that the charge on this capacitor will be the same as the charge on the 3 μF capacitor. μCarrow_forwardIn the pivot assignment, we observed waves moving on a string stretched by hanging weights. We noticed that certain frequencies produced standing waves. One such situation is shown below: 0 ст Direct Measurement ©2015 Peter Bohacek I. 20 0 cm 10 20 30 40 50 60 70 80 90 100 Which Harmonic is this? Do NOT include units! What is the wavelength of this wave in cm with only no decimal places? If the speed of this wave is 2500 cm/s, what is the frequency of this harmonic (in Hz, with NO decimal places)?arrow_forwardFour capacitors are connected as shown in the figure below. (Let C = 12.0 µF.) A circuit consists of four capacitors. It begins at point a before the wire splits in two directions. On the upper split, there is a capacitor C followed by a 3.00 µF capacitor. On the lower split, there is a 6.00 µF capacitor. The two splits reconnect and are followed by a 20.0 µF capacitor, which is then followed by point b. (a) Find the equivalent capacitance between points a and b. µF(b) Calculate the charge on each capacitor, taking ΔVab = 16.0 V. 20.0 µF capacitor µC 6.00 µF capacitor µC 3.00 µF capacitor µC capacitor C µCarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





