
Concept explainers
(a)
The value of
Answer to Problem 74QAP
The value of
Explanation of Solution
Given data:
Formula Used:
Newton's second law:
Calculation:
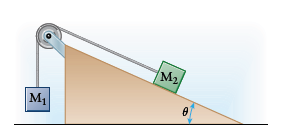
We'll use two different but related coordinate systems for the two blocks. For block
We can draw free-body diagrams and apply Newton's second law in component form for both blocks.
The tension acting on each block will be identical in magnitude.
Since block
Since, both blocks are at rest, which means the acceleration of each block is zero and we can calculate
.
Free-body diagram of
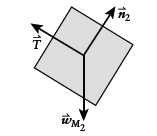
Newton's second law for
Free-body diagram of
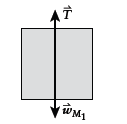
Conclusion:
For two blocks to be in equilibrium the value of
(b)
The magnitude of acceleration of two blocks if the system can move.
Answer to Problem 74QAP
The magnitude of acceleration of two blocks
Explanation of Solution
Given data:
Formula Used:
Newton's second law:
Calculation:
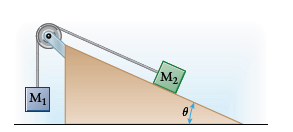
We'll use two different but related coordinate systems for the two blocks. For block
We can draw free-body diagrams and apply Newton's second law in component form for both blocks.
The tension acting on each block will be identical in magnitude.
Since block
Since,
The magnitude of the acceleration will be the same for each block because they are joined together with a string.
Free-body diagram of

Free-body diagram of
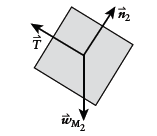
Newton's second law for
Conclusion:
If the system can move the magnitude of acceleration of two blocks is
(c)
The direction of
Answer to Problem 74QAP
The direction of
Explanation of Solution
Given data:
Formula Used:
Newton's second law:
Calculation:
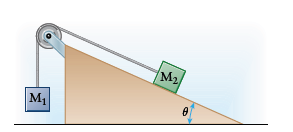
We'll use two different but related coordinate systems for the two blocks. For block
We can draw free-body diagrams and apply Newton's second law in component form for both blocks.
The tension acting on each block will be identical in magnitude.
Since block
Since,
Free-body diagram of
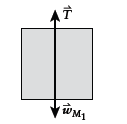
Free-body diagram of
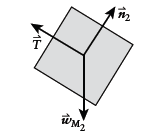
Newton's second law for
Since
Conclusion:
As we have value of
(d)
The distance to which block
Answer to Problem 74QAP
The distance to which block
Explanation of Solution
Given data:
Formula Used:
Newton's second law:
And
Calculation:
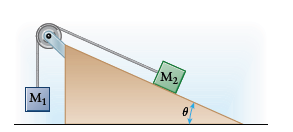
We'll use two different but related coordinate systems for the two blocks. For block
We can draw free-body diagrams and apply Newton's second law in component form for both blocks.
The tension acting on each block will be identical in magnitude.
Since block
Since,
If the acceleration is constant, we can use the constant acceleration equations to calculate how far
Free-body diagram of
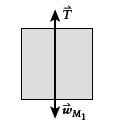
Free-body diagram of
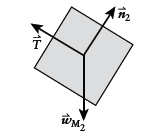
Newton's second law for
By using the constant acceleration equations to calculate how far
Conclusion:
Thus in
Want to see more full solutions like this?
Chapter 4 Solutions
COLLEGE PHYSICS,VOLUME 1
- The angle between the axes of two polarizing filters is 19.0°. By how much does the second filter reduce the intensity of the light coming through the first? I = 0.106 40 xarrow_forwardAn oil slick on water is 82.3 nm thick and illuminated by white light incident perpendicular to its surface. What color does the oil appear (what is the most constructively reflected wavelength, in nanometers), given its index of refraction is 1.43? (Assume the index of refraction of water is 1.33.) wavelength color 675 × nm red (1 660 nm)arrow_forwardA 1.50 μF capacitor is charging through a 16.0 Ω resistor using a 15.0 V battery. What will be the current when the capacitor has acquired 1/4 of its maximum charge? Please explain all stepsarrow_forward
- In the circuit shown in the figure (Figure 1), the 6.0 Ω resistor is consuming energy at a rate of 24 J/s when the current through it flows as shown. What are the polarity and emf of the battery E, assuming it has negligible internal resistance? Please explain all steps. I know you need to use the loop rule, but I keep getting the answer wrong.arrow_forwardIf you connect a 1.8 F and a 2.6 F capacitor in series, what will be the equivalent capacitance?arrow_forwardSuppose that a particular heart defibrillator uses a 1.5 x 10-5 Farad capacitor. If it is charged up to a voltage of 7300 volts, how much energy is stored in the capacitor? Give your answer as the number of Joules.arrow_forward
- The voltage difference across an 8.3 nanometer thick cell membrane is 6.5 x 10-5volts. What is the magnitude of the electric field inside this cell membrane? (Assume the field is uniform, and give your answer as the number of Volts per meter... which is the same as the number of Newtons per Coulomb.)arrow_forwardThree identical capacitors are connected in parallel. When this parallel assembly of capacitors is connected to a 12 volt battery, a total of 3.1 x 10-5 coulombs flows through the battery. What is the capacitance of one individual capacitor? (Give your answer as the number of Farads.)arrow_forwardSuppose you construct your own capacitor by placing two parallel plates at a distance 0.27 meters apart. The plates each have a surface area of 0.64 square meters. What is the capacitance of this setup? (Give your answer as the number of Farads.)arrow_forward
- Draw a diagram with the new arrows. No they do not point all towards the center.arrow_forwardExample In Canada, the Earth has B = 0.5 mŢ, pointing north, 70.0° below the horizontal. a) Find the magnetic force on an oxygen ion (O2) moving due east at 250 m/s b) Compare the |FB| to |FE| due to Earth's fair- weather electric field (150 V/m downward).arrow_forwardFour charges, qa, qb, qa, and qd are fixed at the corners of a square. A charge q that is free to move located at the exact center of the square. Classify the scenarios described according to the force that would be exerted on the center charge q. Assume in each case that q is a positive charge. Do not assume that the fixed charges have equal magnitudes unless the scenario defines such an equality. qa Яс q %b Force is zero Force is to the left Force is to the right Force is undeterminedarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





