Chapter 4, Problem 51P

To determine

Find the force in each bar and mention the force is tension or compression of the bars in the truss.

Explanation of Solution

Assumptions:

• Consider the state of bars as tension (T) where the force is pulling the bar and as compression (C) where the force is pushing the bar.
• The sign of the force in the bar is positive when the force is in tension and negative when the force is in compression.
• Consider the force indicating right side as positive and left side as negative in horizontal components of forces.
• Consider the force indicating upward is taken as positive and downward as negative in vertical components of forces.
• Consider clockwise moment as negative and anti-clock wise moment as positive wherever applicable.

Show the free-body diagram of the entire truss as in Figure 1.

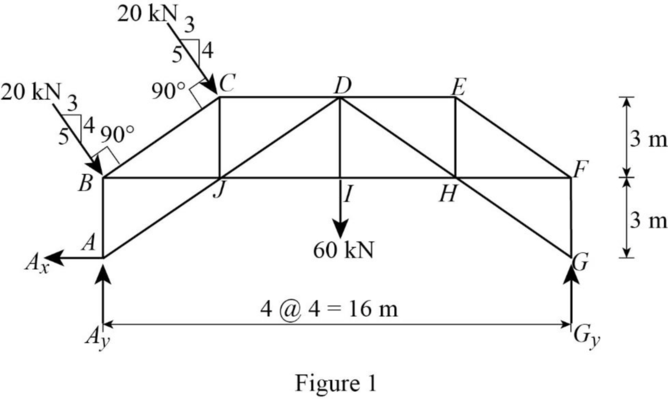
Find the horizontal reaction at point A by resolving the horizontal component of forces.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ -A_x+20\left(\frac{3}{5}\right)+20\left(\frac{3}{5}\right)=0\\ -A_x+12+12=0\\ A_x=24\text{kN}(\leftarrow )\end{array}$

Find the vertical reaction at point G by taking moment about point A.

$\begin{array}{l}{\displaystyle \sum M_A=0}\\ G_y\left(16\right)-60\left(8\right)-20\left(\frac{4}{5}\right)\left(4\right)-20\left(\frac{3}{5}\right)\left(6\right)-20\left(\frac{3}{5}\right)\left(3\right)=0\\ 16G_y-480-64-72-36=0\\ G_y=40.75\text{kN}(\uparrow )\end{array}$

Find the vertical reaction at point A by resolving the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ A_y-20\left(\frac{4}{5}\right)-20\left(\frac{4}{5}\right)-60+G_y=0\\ A_y-16-16-60+40.75=0\\ A_y=51.25\text{kN}(\uparrow )\end{array}$

Consider the joint G;

Show the forces acting at the joint G as in Figure 2.

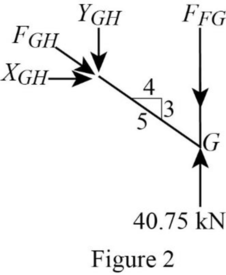
Resolve the horizontal component of forces.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ X_{GH}=0\end{array}$

Use the proportion:

$\begin{array}{l}\frac{X_{GH}}{4}=\frac{Y_{GH}}{3}=\frac{F_{GH}}{5}\\ \frac{0}{4}=\frac{Y_{GH}}{3}=\frac{F_{GH}}{5}\\ Y_{GH}=0\\ F_{GH}=0\end{array}$

Resolve the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ -Y_{GH}-F_{FG}+40.75=0\\ -0-F_{FG}+40.75=0\\ F_{FG}=40.75\text{kN}\left(\text{C}\right)\end{array}$

Consider the joint F;

Show the forces acting at the joint F as in Figure 3.

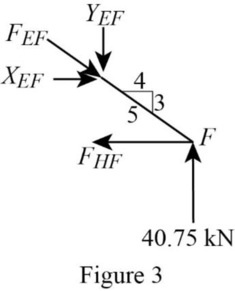
Resolve the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ 40.75-Y_{EF}=0\\ Y_{EF}=40.75\text{kN}\end{array}$

Use the proportion:

$\begin{array}{l}\frac{X_{EF}}{4}=\frac{Y_{EF}}{3}=\frac{F_{EF}}{5}\\ \frac{X_{EF}}{4}=\frac{40.75}{3}=\frac{F_{EF}}{5}\\ X_{EF}=54.33\text{kN}\\ F_{EF}=67.92\text{kN}\left(\text{C}\right)\end{array}$

Resolve the horizontal component of forces.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ X_{EF}-F_{HF}=0\\ 54.33-F_{HF}=0\\ F_{HF}=54.33\text{kN}\left(\text{T}\right)\end{array}$

Consider the joint E;

Show the forces acting at the joint E as in Figure 4.

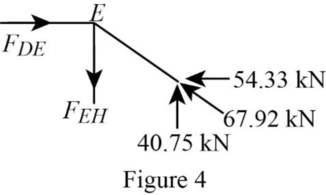
Resolve the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ 40.75-F_{EH}=0\\ F_{EH}=40.75\text{kN}\left(\text{T}\right)\end{array}$

Resolve the horizontal component of forces.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ F_{DE}-54.33=0\\ F_{DE}=54.33\text{kN}\left(\text{C}\right)\end{array}$

Consider the joint H;

Show the forces acting at the joint H as in Figure 5.

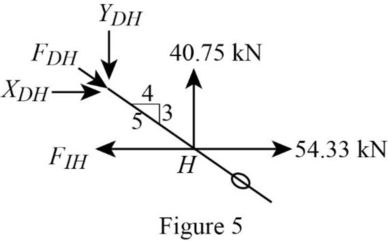
Resolve the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ 40.75-Y_{DH}=0\\ Y_{DH}=40.75\text{kN}\end{array}$

Use the proportion:

$\begin{array}{l}\frac{X_{DH}}{4}=\frac{Y_{DH}}{3}=\frac{F_{DH}}{5}\\ \frac{X_{DH}}{4}=\frac{40.75}{3}=\frac{F_{DH}}{5}\\ X_{DH}=54.33\text{kN}\\ F_{DH}=67.92\text{kN}\left(\text{C}\right)\end{array}$

Resolve the horizontal component of forces.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ -F_{IH}+54.33+X_{DH}=0\\ -F_{IH}+54.33+54.33=0\\ F_{IH}=108.66\text{kN}\left(\text{T}\right)\end{array}$

Consider the joint I;

Show the forces acting at the joint I as in Figure 6.

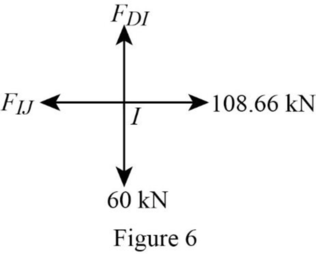
Resolve the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ -60+F_{DI}=0\\ F_{DI}=60\text{kN}\left(\text{T}\right)\end{array}$

Resolve the horizontal component of forces.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ -F_{IJ}+108.66=0\\ F_{IJ}=108.66\text{kN}\left(\text{T}\right)\end{array}$

Consider the joint D;

Show the forces acting at the joint D as in Figure 7.

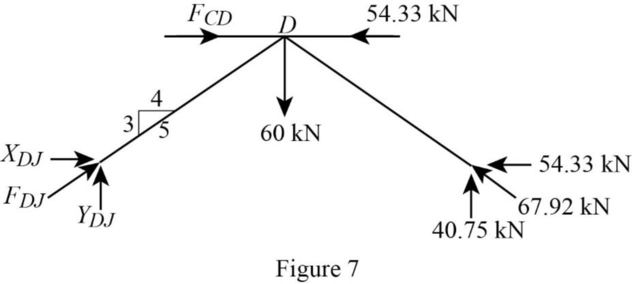
Resolve the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ -60+Y_{DJ}+40.75=0\\ Y_{DJ}=19.25\text{kN}\end{array}$

Use the proportion:

$\begin{array}{l}\frac{X_{DJ}}{4}=\frac{Y_{DJ}}{3}=\frac{F_{DJ}}{5}\\ \frac{X_{DJ}}{4}=\frac{19.25}{3}=\frac{F_{DJ}}{5}\\ X_{DJ}=25.67\text{kN}\\ F_{DJ}=32.08\text{kN}\left(\text{C}\right)\end{array}$

Resolve the horizontal component of forces.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ F_{CD}+X_{DJ}-54.33-54.33=0\\ F_{CD}+25.67-108.66=0\\ F_{CD}=83\text{kN}\left(\text{C}\right)\end{array}$

Consider the joint C;

Show the forces acting at the joint C as in Figure 8.

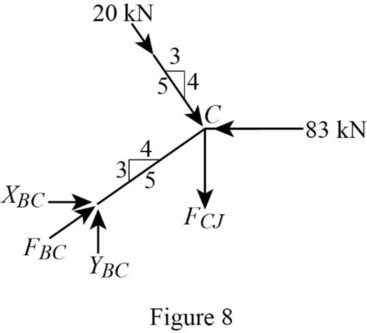
Resolve the horizontal component of forces.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ -83+20\left(\frac{3}{5}\right)+X_{BC}=0\\ X_{BC}=71\text{kN}\end{array}$

Use the proportion:

$\begin{array}{l}\frac{X_{BC}}{4}=\frac{Y_{BC}}{3}=\frac{F_{BC}}{5}\\ \frac{71}{4}=\frac{Y_{BC}}{3}=\frac{F_{BC}}{5}\\ Y_{BC}=53.25\text{kN}\\ F_{BC}=88.75\text{kN}\left(\text{C}\right)\end{array}$

Resolve the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ -20\left(\frac{4}{5}\right)-F_{CJ}+Y_{BC}=0\\ -16-F_{CJ}+53.25=0\\ F_{CJ}=37.25\text{kN}\left(\text{T}\right)\end{array}$

Consider the joint J;

Show the forces acting at the joint J as in Figure 9.

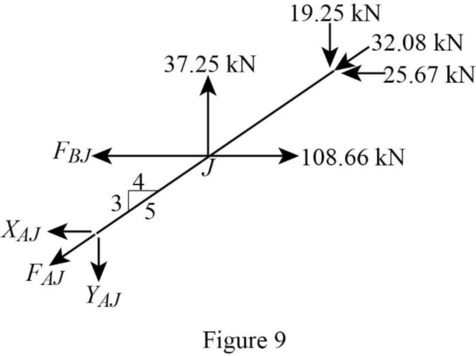
Resolve the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ 37.25-19.25-Y_{AJ}=0\\ Y_{AJ}=18\text{kN}\end{array}$

Use the proportion:

$\begin{array}{l}\frac{X_{AJ}}{4}=\frac{Y_{AJ}}{3}=\frac{F_{AJ}}{5}\\ \frac{X_{AJ}}{4}=\frac{18}{3}=\frac{F_{AJ}}{5}\\ X_{AJ}=24\text{kN}\\ F_{AJ}=30\text{kN}\left(\text{T}\right)\end{array}$

Resolve the horizontal component of forces.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ -F_{BJ}-X_{AJ}-25.67+108.66=0\\ -F_{BJ}-24-25.67+108.66=0\\ F_{BJ}=59\text{kN}\left(\text{T}\right)\end{array}$

Consider the joint A;

Show the forces acting at the joint A as in Figure 10.

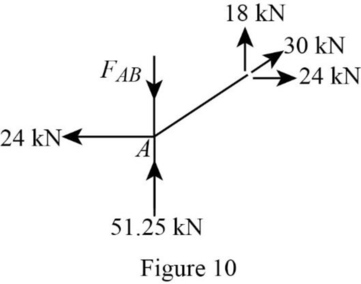
Resolve the vertical component of forces.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ 51.25+18-F_{AB}=0\\ F_{AB}=69.25\text{kN}\left(\text{C}\right)\end{array}$

Show the forces in the bars of the truss as in Figure 11.