
Concept explainers
(a)
Interpretation:
It is to be identified whether the two structures in a given pair are constitutional isomers.
Concept introduction:
Constitutional isomers are also knows as structural isomers having the same molecular formula but differing in their connectivity. In order to identify if the two given structures are constitutional isomers, some steps needs to be followed. Start by identifying the longest continuous chain or largest ring of carbons that contains the
Answer to Problem 4.50P
The two structures in a given pair are not constitutional isomers as they have the same connectivity of atoms.
Explanation of Solution
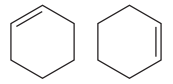
The two structures in the given pair are

Both the above structures contain the largest carbon ring consisting of six carbon atoms. The ring contains one double bond. Both the structures have the same molecular formula.
Both the structures do not have any substituent attached to the root. For cyclic structures containing
The two structures do not differ in their connectivity and, hence, are not constitutional isomers.
Constitutional isomers have the same molecular formula but differ in their connectivity.
(b)
Interpretation:
It is to be identified whether the two structures in a given pair are constitutional isomers.
Concept introduction:
Constitutional isomers are also knows as structural isomers having the same molecular formula but differing in their connectivity. In order to identify if the two given structures are constitutional isomers, some steps needs to be followed. Start by identifying the longest continuous chain or largest ring of carbons that contains the functional group. Number the carbon atoms involved in the root including the functional group such that the carbon atoms in the functional group receive the lowest possible locator numbers. Also, the substituents attached to the root get the lower possible locator numbers. If two given structures differ in the size of the longest continuous chain, ring or the numbers assigned to the carbon atoms involved in the multiple bonds, the numbers assigned to the carbon atoms to which any substituent is attached, or the identities of the substituents attached to the same-numbered carbon atoms, then the two structures must be constitutional isomers of each other. Otherwise, the molecules have the same connectivity and are not constitutional isomers.
Answer to Problem 4.50P
The two structures in a given pair are constitutional isomers as they have different connectivity of atoms.
Explanation of Solution
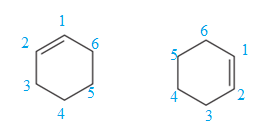
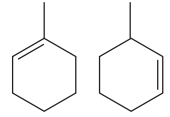
The two structures in the given pair are

Both the above structures contain the largest carbon ring consisting of six carbon atoms. The ring contains one double bond and one methyl substituent. Both the structures have the same molecular formula. For cycloalkenes, the carbon atoms bearing
For the structure on the left, the numbering can be done so as to give the lowest possible number for the substituent attached. It can be done as
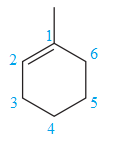
For the structure on the right, the numbering can be done so as to give the lowest possible number for the substituent attached. It can be done as
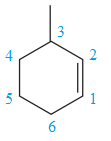
Note that the position of the substituent is different in both the structures. Thus, the two must be constitutional isomers of each other.
Constitutional isomers have the same molecular formula but differ in their connectivity.
(c)
Interpretation:
It is to be identified whether the two structures in a given pair are constitutional isomers.
Concept introduction:
Constitutional isomers are also knows as structural isomers having the same molecular formula but differing in their connectivity. In order to identify if the two given structures are constitutional isomers, some steps needs to be followed. Start by identifying the longest continuous chain or largest ring of carbons that contains the functional group. Number the carbon atoms involved in the root including the functional group such that the carbon atoms in the functional group receive the lowest possible locator numbers. Also, the substituents attached to the root get the lower possible locator numbers. If two given structures differ in the size of the longest continuous chain, ring or the numbers assigned to the carbon atoms involved in the multiple bonds, the numbers assigned to the carbon atoms to which any substituent is attached, or the identities of the substituents attached to the same-numbered carbon atoms, then the two structures must be constitutional isomers of each other. Otherwise, the molecules have the same connectivity and are not constitutional isomers.
Answer to Problem 4.50P
The two structures in a given pair are not constitutional isomers as they have the same connectivity of atoms.
Explanation of Solution
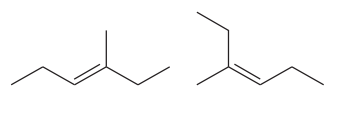
The two structures in the given pair are

The longest continuous chain of carbon atoms in each molecule has six carbons. The molecular formula for both the structures is the same. The carbon atoms are numbered 1 through 6 so that the first methyl group is encountered on C3 carbon atom as shown below:
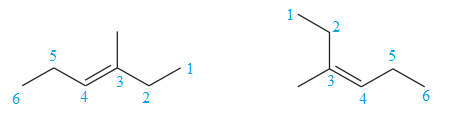
Because the methyl group is attached to C3 carbon atoms in both the molecules, the molecules have the same connectivity of atoms and therefore are not constitutional isomers.
Constitutional isomers have the same molecular formula but differ in their connectivity.
(d)
Interpretation:
It is to be identified whether the two structures in a given pair are constitutional isomers.
Concept introduction:
Constitutional isomers are also knows as structural isomers having the same molecular formula but differing in their connectivity. In order to identify if the two given structures are constitutional isomers, some steps needs to be followed. Start by identifying the longest continuous chain or largest ring of carbons that contains the functional group. Number the carbon atoms involved in the root including the functional group such that the carbon atoms in the functional group receive the lowest possible locator numbers. Also, the substituents attached to the root get the lower possible locator numbers. If two given structures differ in the size of the longest continuous chain, ring or the numbers assigned to the carbon atoms involved in the multiple bonds, the numbers assigned to the carbon atoms to which any substituent is attached, or the identities of the substituents attached to the same-numbered carbon atoms, then the two structures must be constitutional isomers of each other. Otherwise, the molecules have the same connectivity and are not constitutional isomers.
Answer to Problem 4.50P
The two structures in a given pair are not constitutional isomers as they have the same connectivity of atoms.
Explanation of Solution
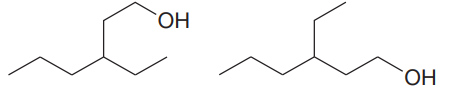
The two structures in the given pair are

The longest continuous chain of carbon atoms in each molecule has six carbons. The molecular formula for both the structures is the same. The carbon atoms are numbered 1 through 6 so that the carbon atoms to which
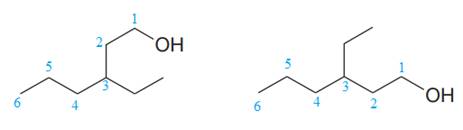
Because the ethyl group is attached to C3 carbon atoms in both the molecules, the molecules have the same connectivity of atoms and therefore are not constitutional isomers.
Constitutional isomers have the same molecular formula but differ in their connectivity.
(e)
Interpretation:
It is to be identified whether the two structures in a given pair are constitutional isomers.
Concept introduction:
Constitutional isomers are also knows as structural isomers having the same molecular formula but differing in their connectivity. In order to identify if the two given structures are constitutional isomers, some steps needs to be followed. Start by identifying the longest continuous chain or largest ring of carbons that contains the functional group. Number the carbon atoms involved in the root including the functional group such that the carbon atoms in the functional group receive the lowest possible locator numbers. Also, the substituents attached to the root get the lower possible locator numbers. If two given structures differ in the size of the longest continuous chain, ring or the numbers assigned to the carbon atoms involved in the multiple bonds, the numbers assigned to the carbon atoms to which any substituent is attached, or the identities of the substituents attached to the same-numbered carbon atoms, then the two structures must be constitutional isomers of each other. Otherwise, the molecules have the same connectivity and are not constitutional isomers.
Answer to Problem 4.50P
The two structures in a given pair are constitutional isomers as they have different connectivity of atoms.

Explanation of Solution
The two structures in the given pair are

Both the above structures contain the largest carbon ring consisting of six carbon atoms. The ring contains double bonds. Both the structures have the same molecular formula.
Both the structures do not have any substituent attached to the root. For cyclic structures containing

Note that there are three double bonds for the ring on the left and two for the ring on the right. The two structures differ in their connectivity and, hence, are constitutional isomers.
Constitutional isomers have the same molecular formula but differ in their connectivity.
(g)
Interpretation:
It is to be identified whether the two structures in a given pair are constitutional isomers.
Concept introduction:
Constitutional isomers are also knows as structural isomers having the same molecular formula but differing in their connectivity. In order to identify if the two given structures are constitutional isomers, some steps needs to be followed. Start by identifying the longest continuous chain or largest ring of carbons that contains the functional group. Number the carbon atoms involved in the root including the functional group such that the carbon atoms in the functional group receive the lowest possible locator numbers. Also, the substituents attached to the root get the lower possible locator numbers. If two given structures differ in the size of the longest continuous chain, ring or the numbers assigned to the carbon atoms involved in the multiple bonds, the numbers assigned to the carbon atoms to which any substituent is attached, or the identities of the substituents attached to the same-numbered carbon atoms, then the two structures must be constitutional isomers of each other. Otherwise, the molecules have the same connectivity and are not constitutional isomers.
Answer to Problem 4.50P
The two structures in a given pair are not constitutional isomers as they have different molecular formula.
Explanation of Solution
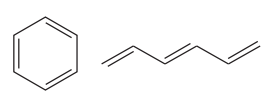
The two structures in the given pair are

Out of the two gives compounds, one is a ring of six carbon atoms, while the other is a straight chain of six carbon atoms. Though both the structures have the root with six carbon
Constitutional isomers have the same molecular formula but differ in their connectivity.
(h)
Interpretation:
It is to be identified whether the two structures in a given pair are constitutional isomers.
Concept introduction:
Constitutional isomers are also knows as structural isomers having the same molecular formula but differing in their connectivity. In order to identify if the two given structures are constitutional isomers, some steps needs to be followed. Start by identifying the longest continuous chain or largest ring of carbons that contains the functional group. Number the carbon atoms involved in the root including the functional group such that the carbon atoms in the functional group receive the lowest possible locator numbers. Also, the substituents attached to the root get the lower possible locator numbers. If two given structures differ in the size of the longest continuous chain, ring or the numbers assigned to the carbon atoms involved in the multiple bonds, the numbers assigned to the carbon atoms to which any substituent is attached, or the identities of the substituents attached to the same-numbered carbon atoms, then the two structures must be constitutional isomers of each other. Otherwise, the molecules have the same connectivity and are not constitutional isomers.
Answer to Problem 4.50P
The two structures in a given pair are constitutional isomers as they have different connectivity of atoms.
Explanation of Solution
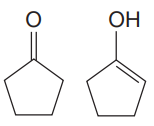
The two structures in the given pair are

Both the above structures contain the largest carbon ring consisting of five carbon atoms. Both the structures have the same molecular formula.
The ring on the left can be numbered in such a way so that the double bonded carbon atom gets the lowest possible locator number.
The ring on the right can be numbered in such a way that each of the double bonded carbon atom gets C1 and C2 numbers. The numbering for both the structures is shown below:
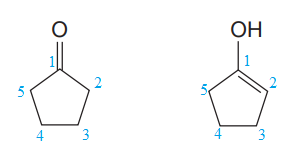
The ring on the left has
Note that the connectivity of the two structures is different.
Thus, the two must be constitutional isomers of each other.
Constitutional isomers have the same molecular formula but differ in their connectivity.
Want to see more full solutions like this?
Chapter 4 Solutions
ORGANIC CHEMISTRY PRINCIPLES & MECHANISM
- 19) Which metal is most commonly used in galvanization to protect steel structures from oxidation? Lead a. b. Tin C. Nickel d. Zinc 20) The following molecule is an example of a: R₁ R2- -N-R3 a. Secondary amine b. Secondary amide c. Tertiary amine d. Tertiary amidearrow_forwardpls helparrow_forwardIndicate the product of the reaction OH OH CH3-CC- Ph + H2SO4 a 20°C | CH3 Pharrow_forward
- 35) Complete the following equation by drawing the line the structure of the products that are formed. Please note that in some cases more than one product is possible. You must draw all possible products to recive full marks! a. ethanol + 2-propanol + H2SO4 → b. OH conc. H2SO4 CH2 H3C CH + K2Cr2O7 C. d. H3C A pressure CH3 + H2 CH Pt catalystarrow_forward21) The rate of reaction depends upon: a. the concentration and nature of reactants b. the temperature of the reaction C. whether or not a catalyst was used d. all of the above 22) A Maxwell-Boltzmann curve shows the distribution of molecular energies in a reaction system. When the temperature in this system is increased, the peak is a. higher and further to the right. b. higher and further to the left. c. lower and further to the right. d. lower and further to the left. 23) Which of the following correctly describes the reaction represented by the reaction below? CaCO3 (s) + energy → CaO (s) + CO2 (g) a. It is exothermic and the potential energy is greater in the reactants than the products. b. c. It is exothermic and the potential energy is greater in the products than the reactants. It is endothermic and the potential energy is greater in the products than the reactants. d. It is endothermic and the potential energy is equal for the products and reactants.arrow_forwardpls helparrow_forward
- 27) Draw the energy level diagram and write the full and shorthand electron configuration for a neutral sulfur atom.arrow_forwardIndicate whether these compounds are isomers, enantiomers, or tautomers. OCH OCH محمد ممدarrow_forward30) Substance A to E below are listed with several of their properties. The identities of the substances are identified in random order below: Iron, ethane, ethanol, sodium nitrate, graphite First classify each substance as either a polar covalent compound, non-polar covalent compound, ionic compound, metallic solid, or network solid. Write your predictions in the sixth coloumn of the chart, under "type of substance." Then, identify the identity of the substance in the last coloumn. Substance Melting Point Boiling Point Solubility in H₂O Electrical Conductivity Type of Substance Identity of Substance (°C) (°C) as: Solid, Liquids, Solution A -182 -88 Insoluble No/No/- B 1538 2862 Insoluble Yes/Yes/- C 308 380 Soluble Yes/Yes/Yes Ꭰ 3456 Insoluble No/-/- E -114 78 Soluble No/No/Noarrow_forward
 Living By Chemistry: First Edition TextbookChemistryISBN:9781559539418Author:Angelica StacyPublisher:MAC HIGHERChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co
Living By Chemistry: First Edition TextbookChemistryISBN:9781559539418Author:Angelica StacyPublisher:MAC HIGHERChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co Chemistry for Today: General, Organic, and Bioche...ChemistryISBN:9781305960060Author:Spencer L. Seager, Michael R. Slabaugh, Maren S. HansenPublisher:Cengage Learning
Chemistry for Today: General, Organic, and Bioche...ChemistryISBN:9781305960060Author:Spencer L. Seager, Michael R. Slabaugh, Maren S. HansenPublisher:Cengage Learning
 Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning





