
Concept explainers
Calculate the gas pressure inside the platinum capsule after
Answer to Problem 4.35P
Gas pressure is
Explanation of Solution
When Radium-226 decay, it emits a particles each a particle is a helium nucleus with 2 electrons and forms helium gas which produces pressure in a capsule.
226 Ra emits 4 alpha particles per decay immediately after secular equilibrium and there is the formation of the fifth a particle.
The fraction of
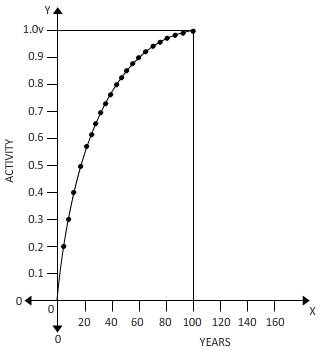
Above carve shows a fraction of a to helium over 100 years.
Fraction=Area under curve/Total area
=
Integrating from
Fraction=
Four alpha particles emitted over
We know that,
To calculate the fraction of decay
Rearranging, (1) and (2)
Hence
To calculate helium atoms formed over
We have,
The dimension of the capsule,
The molecular weight of RaBr2,
The volume of RaBr2 is,
Volume available for gas=volume of capsule-volume of RaBr2
According to Ideal gas low
The pressure of helium formed by the decay of radium is 22.3 atmospheres. But originally capsule contains an air of 1 atmospheric pressure. Hence this initial pressure must be considered.
Thus, pressure=
Conclusion:
We can conclude about this problem that, when Radium-226 decays. It emits a particles having helium nucleus with two electrons and produces helium gas. Ideal gas law is used to calculate the pressure of helium gas. The gas pressure inside the capsule is 23.3 atm due to the formation of helium gas by the decay of radium.
Want to see more full solutions like this?
Chapter 4 Solutions
EBK INTRODUCTION TO HEALTH PHYSICS, FIF
- Pls help ASAParrow_forwardFind the integral expression for the magnetic force on a wire carrying 3.5 amps current on the z axis with length2 meters on end at the origin and the other at z=4. Magnetic field is B = 4(zy+4) i - (z-3) j + 20(x+2)/(z-3) k.Don’t take the integral. Integral should contain only x-y-z as variables not rarrow_forwardPls help ASAParrow_forward
- 9. Light of wavelength 442 nm is sent through a single slit with a width of 884 nm. At what angle does the first dark fringe occur? a. 30.0° b. 45.0° C. 60.0° d. 90.0° 10. Light travels through a single-slit and forms an interference pattern. The spacing of the dark fringes on one side of the pattern is 1.44 cm. What is the width of the central maximum? a. 0.720 cm 1.44 cm b. C. 2.88 cm d. 4.32 cmarrow_forwardPls help ASAParrow_forwardd. when the index of refraction of medium A is equal to the index of refraction of medium B 7. What is the term for the bending of a wave front as it passes an obstacle? a. interference b. reflection C. d. diffraction refraction 8. A ray of light travels from air into a soap film on a layer of glass, as shown right. Which statement about ray 1 is true? a. There is no inversion at either surface. b. There is an inversion the surface between air and soap, but not soap and glass. C. There is no inversion at the surface between air and soap, incident light ray 1 ray 2 ray 3 but there is one at the surface between soap and glass. d. There is an inversion at both surfaces. air = nair 1.00 soap film nfilm = 1.35 glass = nglass 1.50arrow_forward
- A circular wire with radius 0.4 meters in on x-y plane. There is a constant Magnetic field with 14T strengthtowards z-axis. Find the magnitude of the electromotive force and the direction of the current for a) B decreasesto 10T in 5 seconds. B) B is rotated by 45 degrees and the area doubles in 4 seconds.arrow_forwardWrite the expression for the magnetic flux inside a region om x-z plane at y=0 bounded by z=3x z=0 x=5 x=7due to a magnetic field B = f(x,y,z) i +g(x,y,z) j + h(x,y,z) karrow_forwardExplain mutual inductance of two loops facing one another and compare with one loop inside the other.arrow_forward
- Two very long wires carry each 3 amps current in the same direction along the z-axis (outward). First is at x=0y=0 current is upward. Second at x=0 y=3 current is also upward. Find the net magnetic field at x=4 y=3.arrow_forwardFind the integral expression for the magnetic field at x=5 y=6 due to a wire on the x axis with length 5 meters onend at x=0 and the other at x=5. Don’t take the integralarrow_forwardTwo very long wires carry current along y-axis. First is at x=0 0.45 amps current is upward. Second at x=5 currentwith 0.65 amps current downward. Find the net magnetic a) Two meters to the left of the first wire. b) Twometers to the right of the first wire. a) Two meters to the right of the second wire. b) Two meters to the right ofthe second wire.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





