
Education The following table shows the enrollments for the four divisions of a college. There are 50 new overhead projectors that are to be apportioned among the divisions based on the enrollments.
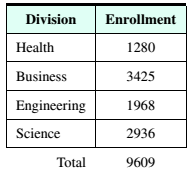
a. Use the Hamilton method to determine the number of projectors to be apportioned to each division.
b. Use the Jefferson method to determine the number of projectors to be apportioned to each division.
c. Use the Webster method to determine the number of projectors to be apportioned to each division.
(a)
Use the Hamilton method to determine tile number of projectors to be apportioned to each division.
Answer to Problem 1RE
Hence, the projectors to be apportioned each division Health, Business, Engineering, and Science is
Explanation of Solution
Given Information:
Number of overhead projectors
Concept used:
Calculation:
Since there is a total 50 new overhead projectors should be apportioned standard divisor is calculated by total number of enrollments divided by total number of new over head projectors that are to be apportioned, formula for standard divisor is,
Therefore,
Under the Hamilton plan, divide the enrollments of each division by the standard divisor and round the quotient down to a whole number
| Divisions | Enrollments | Quotient | Standard Quota |
| Health | | | |
| Business | | | |
| Engineering | | | |
| Science | | | |
| Total | | ||
When this happen the Hamilton plan calls for revisiting the calculation of the quotients and assigning an additional representative to the divisions with the largest decimal remaindeí process is continued until the number of representatives equals the number required by divisions. For divisions we have.
| Divisions | Enrollments | Quotient | Standard Quota | Number of overhead projectors |
| Health | | | | |
| Business | | | | |
| Engineering | | | | |
| Science | | | | |
| | |
Hence, the projectors to be apportioned each division Health, Business, Engineering, and Science is
Conclusion:
Hence, the projectors to be apportioned each division Health, Business, Engineering, and Science is
(b)
Use the Jefferson method to determine the number of projectors to be apportioned to each division.
Answer to Problem 1RE
The projectors to be apportioned each division Health, Business, Engineering, and Science is
Explanation of Solution
Given Information:
| Division | Enrollment |
| Health | |
| Business | |
| Engineering | |
| Science | |
| Total | |
Concept used:
Calculation:
For Jefferson plan we consider modified standard divisor by trial and error is
| Divisions | Enrollments | Quotient | Standard Quota |
| Health | | | |
| Business | | | |
| Engineering | | | |
| Science | | | |
| Total | | ||
Hence, the projectors to be apportioned each division Health, Business, Engineering, and Science is
Conclusion:
The projectors to be apportioned each division Health, Business, Engineering, and Science is
(c)
Use the Webster method to determine the number of projectors to be apportioned to each division.
Answer to Problem 1RE
The projectors to be apportioned each division Health, Business, Engineering, and
Science is
Explanation of Solution
Given Information:
Webster method
Concept used:
Webster method includes Enrollment, Quotient and number of overhead projects.
Calculation:
Now use Webster method to determine the number of projectors to be apportioned therefore,
| Divisions | Enrollments | Quotient | Standard Quota | Number of overhead projectors |
| Health | | | | |
| Business | | | | |
| Engineering | | | | |
| Science | | | | |
| Total | | | ||
Hence, the projectors to be apportioned each division Health, Business, Engineering, and
Science is
Conclusion:
The projectors to be apportioned each division Health, Business, Engineering, and
Science is
Want to see more full solutions like this?
Chapter 4 Solutions
Bundle: Mathematical Excursions, Loose-leaf Version, 4th + WebAssign Printed Access Card
- 3 2 Find: ƒ(1) lim f(x) 14-x 2 ƒ(2) lim f(x) x-2- lim f(x) x+2+ lim f(x) x→4 3 y=f(x)arrow_forwardFor each graph below, state whether it represents a function. Graph 1 24y Graph 2 Graph 3 4 2 -8 -6 -4 -2 -2 2 4 6 Function? ○ Yes ○ No ○ Yes ○ No Graph 4 Graph 5 8 Function? Yes No Yes No -2. ○ Yes ○ No Graph 6 4 + 2 4 -8 -6 -4 -2 2 4 6 8 Yes -4++ Noarrow_forwardStudents were asked to simplify the expression (secØ - cosØ)/secØ Two students' work is given.Student A: step 1 secØ/secØ - cosØ/secØstep 2 cosØ/1 - (1/cosØ)step 3 1 - cos^2Østep 4 sin^2ØStudent B: step 1 (1/cosØ)-cosØ)/secØstep 2 (1 - cos^2Ø/cosØ)/secØstep 3 sin^2Ø/cos^2Østep 4 tan^2ØPart A: Which student simplified the expression incorrectly? Explain the errors that were made or the formulas that were misused.Part B: Complete the student's solution correctly, beginning with the location of the error.arrow_forward
- Although 330° is a special angle on the unit circle, Amar wanted to determine its coordinates using the sum and difference formulas.Part A: Determine cos 330° using the cosine sum identity. Be sure to include all necessary work.Part B: Determine sin 330° using the sine difference identity. Be sure to include all necessary work.arrow_forwardA public health researcher is studying the impacts of nudge marketing techniques on shoppers vegetablesarrow_forward4. Let A {w, e, s, t, f, i, e, l, d, s, t, a, t, e}. (a) How many different words (they do not have to make sense) can you spell with the letters in A? (b) Is your answer from above the same as the cardinality of the powerset of A, i.e. of P(A)? (c) What is |A|?arrow_forward
- what can the answer be pls helparrow_forward5. How many numbers can you make out of the digits 1, 2, 3, 4, 6 if the rule is that every digit has to be larger than the digit preceding it? For example 124 is ok, 122 is not ok. Every digit can be used only once, but you do not have to use every digit. A tree might help.arrow_forward5 plsarrow_forward
- 8 pls show workarrow_forward7 pls show workarrow_forwardThe director of admissions at Kinzua University in Nova Scotia estimated the distribution of student admissions for the fall semester on the basis of past experience. Admissions Probability 1,100 0.5 1,400 0.4 1,300 0.1 Click here for the Excel Data File Required: What is the expected number of admissions for the fall semester? Compute the variance and the standard deviation of the number of admissions. Note: Round your standard deviation to 2 decimal places.arrow_forward
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
