Chapter 4, Problem 1RCC

(a) Write an expression for a Riemann sum of a function f on an interval [a, b]. Explain the meaning of the notation that you use.

(b) If $f\left(x\right)⩾0$, what is the geometric interpretation of a Riemann sum? Illustrate with a diagram.

(c) If f(x) takes on both positive and negative values, what is the geometric interpretation of a Riemann sum? Illustrate with a diagram.

To determine

To find: The expression for a Riemann sum of a function $f$.

Answer to Problem 1RCC

The expression for a Riemann sum of a function f is ${\displaystyle \sum _{i=1}^{n}f\left(x_i^{*}\right)\Delta x}$.

Explanation of Solution

The Riemann sum of a function f is the method to find the total area underneath a curve.

The area under the curve dividedas n number of approximating rectangles. Hence the Riemann sum of a function f is the sum of the area of the all individual rectangles.

$R={\displaystyle \sum _{i=1}^{n}f\left(x_i^{*}\right)\Delta x}$

Here, $x_i{}^{*}$ is a point in the $i$ subinterval $\left[x_{i-1},x_i\right]$ and $\Delta x$ is the length of the sub intervals.

Thus, the expression for a Riemann sum of a function f is ${\displaystyle \sum _{i=1}^{n}f\left(x_i^{*}\right)\Delta x}$.

To determine

To define: The geometric interpretation of a Riemann sum with diagram.

Explanation of Solution

Given information:

Consider the condition for the function $f\left(x\right)\ge 0$

Explanation:

The function $f\left(x\right)\ge 0$ represents that the function is in the first quadrant of the graph.

Sketch the curve $f\left(x\right)$ in the first quadrant and then separate the area under the curve with n number approximating rectangles.

Show the curve as in Figure 1.

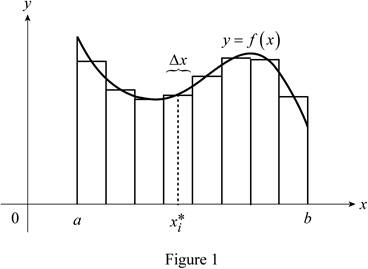
Refer to Figure 1

The function $f\left(x\right)$ is positive. Hence the sum of areas of rectangles underneath the curve is the Riemann sum.

Thus, the geometric interpretation of a Riemann sum of $f\left(x\right)\ge 0$ is defined.

To determine

To define: The geometric interpretation of a Riemann sum, if the function $f\left(x\right)$ takes on both positive and negative values.

Explanation of Solution

Given information:

The function $f\left(x\right)$ takes on both positive and negative values.

Explanation:

The function $f\left(x\right)$ takes on both positive and negative values represents that the function is in the first and fourth quadrant of the graph.

Sketch the curve $f\left(x\right)$ in the first and third quadrant and then divide the area under the curve and above the curve with n number approximating rectangles.

Show the curve as in Figure 2.

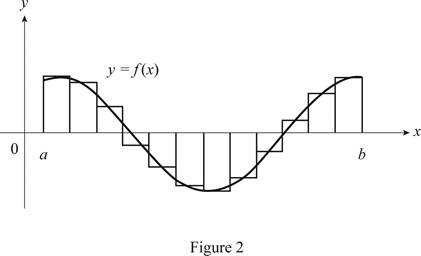
Refer figure 2,

The Riemann sum is the difference of areas of approximating rectangles above and below the x-axis

Therefore, the geometric interpretation of a Riemann sum is defined, if $f\left(x\right)$ has both positive and negative values.