
Concept explainers
For Exercises 1-14,
a. Write the domain.
b. Write the range.
c. Find the x-intercept(s).
d. Find the y-intercept.
e. Determine the asymptotes if applicable.
f. Determine the intervals over which the function is increasing.
g. Determine the intervals over which the function is decreasing.
h. Match the function with its graph.
1.
(a)
To find the domainof the function
Answer to Problem 1PRE
The domain of function
Explanation of Solution
Given: The function
Formula Used:
The domain of a function is the set of input or argument values for which the function is real and defined.
Calculation:
The function has no undefined points nor domain constraints. So, the domain will be all real numbers.
Therefore, the domain is
Conclusion:
The domain of function
(b)
To find the range of the function
Answer to Problem 1PRE
The range of function
Explanation of Solution
Given: The function
Formula Used:
The range of a function is the set of values of the dependent variable for which a function is defined.
Calculation:
Here, the function
Conclusion:
The range of function
(c)
To find x-intercept of the function
Answer to Problem 1PRE
There is no x-intercept
Explanation of Solution
Given: Function -
Formula Used:
x-intercept is a point on the graph where
Calculation:
The y-intercept of a function is obtained at the point when
But,
So, there is no such value of x which gives
Conclusion:
Hence, there are no x-axis interception points.
(d)
To find the y-intercept of the function
Answer to Problem 1PRE
The y-intercept of function
Explanation of Solution
Given: Function -
Formula Used:
y-intercept is a point on the graph where
Calculation:
Function is given as
For y-intercept,
And
Thus, y-axis interception point is
Conclusion:
The y-intercept of function
(e)
To find Asymptotes (if applicable) of the function
Answer to Problem 1PRE
There are no asymptotes of the function
Explanation of Solution
Given: Function -
Formula Used:
If
Calculation:
Given function is
There are no asymptotes as polynomial functions of degree 1 or higher can’t have asymptotes.
Conclusion:
Hence, there is no asymptote for the function
(f)
To find intervals over which the function
Answer to Problem 1PRE
Function is not an increasing function.
Explanation of Solution
Given: Function -
Formula Used:
If
Calculation:
Derivative of
Thus, the function is not increasing.
Conclusion:
Hence, function is not an increasing function
(g)
To find intervals over which the function
Answer to Problem 1PRE
Function is not a decreasing function.
Explanation of Solution
Given: Function -
Formula Used:
If
Calculation:
Derivative of
Thus, the function is not decreasing.
Conclusion:
Hence, the function is not a decreasing function
(h)
To graph the function
Explanation of Solution
Given: Function -
Graph:
Given function is
When
When
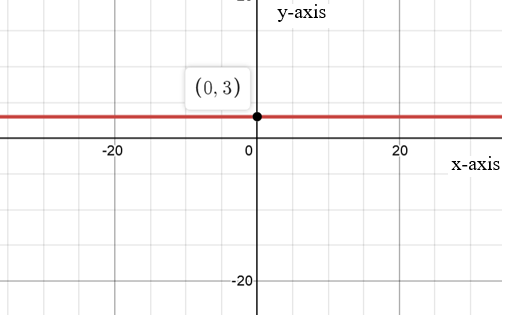
Thus, the graph is matched with the function
Want to see more full solutions like this?
Chapter 4 Solutions
ALEKS ACCESS CODE 52 WEEK
- Question 5. Let A, B, C ben x n-matrices, S is nonsigular. If A = S-1 BS, show that det (A) = det (B) Question 6. For what values of k is the matrix A = (2- k -1 -1 2) singular? karrow_forward1 4 5 Question 3. Find A-1 (if exists), where A = -3 -1 -2 2 3 4 Question 4. State 4 equivalent conditions for a matrix A to be nonsingulararrow_forwardHow long is a guy wire reaching from the top of a 15-foot pole to a point on the ground 9-feet from the pole? Question content area bottom Part 1 The guy wire is exactly feet long. (Type an exact answer, using radicals as needed.) Part 2 The guy wire is approximatelyfeet long. (Round to the nearest thousandth.)arrow_forward
- Question 6 Not yet answered Marked out of 5.00 Flag question = If (4,6,-11) and (-12,-16,4), = Compute the cross product vx w karrow_forwardConsider the following vector field v^-> (x,y): v^->(x,y)=2yi−xj What is the magnitude of the vector v⃗ located in point (13,9)? [Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places]arrow_forwardQuestion 4 Find the value of the first element for the first row of the inverse matrix of matrix B. 3 Not yet answered B = Marked out of 5.00 · (³ ;) Flag question 7 [Provide your answer as an integer number (no fraction). For a decimal number, round your answer to 2 decimal places] Answer:arrow_forward
- Question 2 Not yet answered Multiply the following Matrices together: [77-4 A = 36 Marked out of -5 -5 5.00 B = 3 5 Flag question -6 -7 ABarrow_forwardAssume {u1, U2, u3, u4} does not span R³. Select the best statement. A. {u1, U2, u3} spans R³ if u̸4 is a linear combination of other vectors in the set. B. We do not have sufficient information to determine whether {u₁, u2, u3} spans R³. C. {U1, U2, u3} spans R³ if u̸4 is a scalar multiple of another vector in the set. D. {u1, U2, u3} cannot span R³. E. {U1, U2, u3} spans R³ if u̸4 is the zero vector. F. none of the abovearrow_forwardSelect the best statement. A. If a set of vectors includes the zero vector 0, then the set of vectors can span R^ as long as the other vectors are distinct. n B. If a set of vectors includes the zero vector 0, then the set of vectors spans R precisely when the set with 0 excluded spans Rª. ○ C. If a set of vectors includes the zero vector 0, then the set of vectors can span Rn as long as it contains n vectors. ○ D. If a set of vectors includes the zero vector 0, then there is no reasonable way to determine if the set of vectors spans Rn. E. If a set of vectors includes the zero vector 0, then the set of vectors cannot span Rn. F. none of the abovearrow_forward
- Which of the following sets of vectors are linearly independent? (Check the boxes for linearly independent sets.) ☐ A. { 7 4 3 13 -9 8 -17 7 ☐ B. 0 -8 3 ☐ C. 0 ☐ D. -5 ☐ E. 3 ☐ F. 4 THarrow_forward3 and = 5 3 ---8--8--8 Let = 3 U2 = 1 Select all of the vectors that are in the span of {u₁, u2, u3}. (Check every statement that is correct.) 3 ☐ A. The vector 3 is in the span. -1 3 ☐ B. The vector -5 75°1 is in the span. ГОЛ ☐ C. The vector 0 is in the span. 3 -4 is in the span. OD. The vector 0 3 ☐ E. All vectors in R³ are in the span. 3 F. The vector 9 -4 5 3 is in the span. 0 ☐ G. We cannot tell which vectors are i the span.arrow_forward(20 p) 1. Find a particular solution satisfying the given initial conditions for the third-order homogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y(3)+2y"-y-2y = 0; y(0) = 1, y'(0) = 2, y"(0) = 0; y₁ = e*, y2 = e¯x, y3 = e−2x (20 p) 2. Find a particular solution satisfying the given initial conditions for the second-order nonhomogeneous linear equation given below. (See Section 5.2 in your textbook if you need a review of the subject.) y"-2y-3y = 6; y(0) = 3, y'(0) = 11 yc = c₁ex + c2e³x; yp = −2 (60 p) 3. Find the general, and if possible, particular solutions of the linear systems of differential equations given below using the eigenvalue-eigenvector method. (See Section 7.3 in your textbook if you need a review of the subject.) = a) x 4x1 + x2, x2 = 6x1-x2 b) x=6x17x2, x2 = x1-2x2 c) x = 9x1+5x2, x2 = −6x1-2x2; x1(0) = 1, x2(0)=0arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL





