
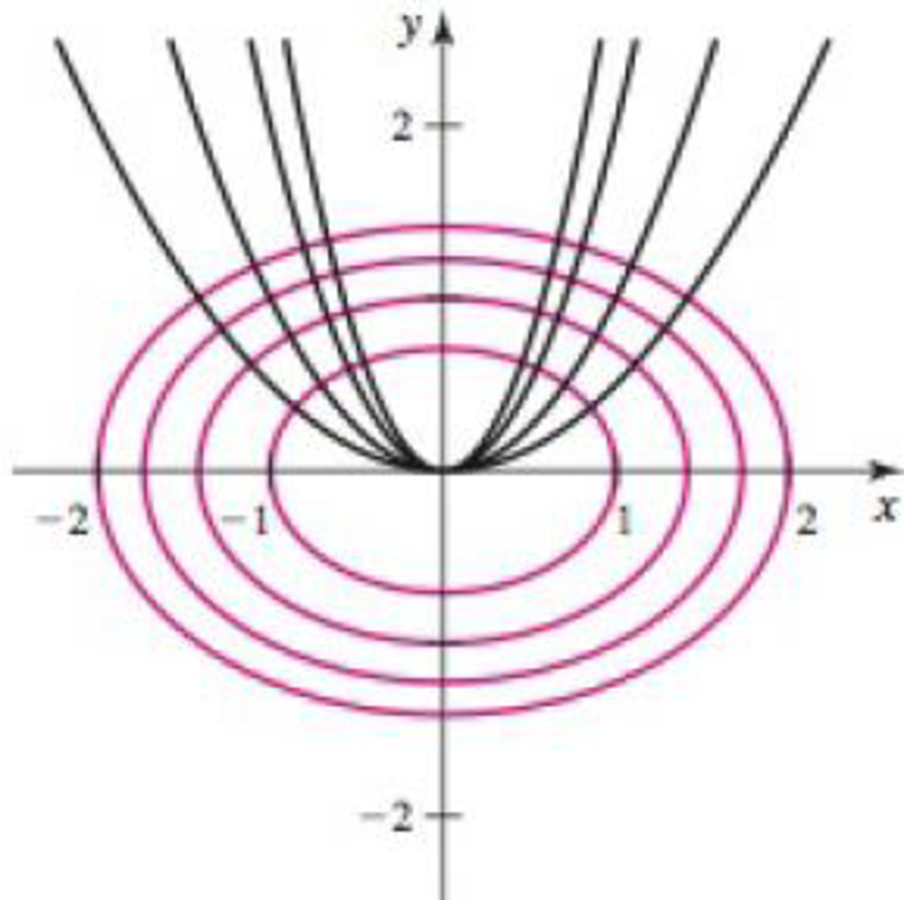
Orthogonal trajectories Two curves are orthogonal to each other if their tangent lines are perpendicular at each point of intersection (recall that two lines are perpendicular to each other if their slopes are negative reciprocals). A family of curves forms orthogonal trajectories with another family of curves if each curve in one family is orthogonal to each curve in the other family. For example, the parabolas y = cx2 form orthogonal trajectories with the family of ellipses x2 + 2y2 = k, where c and k are constants (see figure).
Find dy/dx for each equation of the following pairs. Use the derivatives to explain why the families of curves form orthogonal trajectories.
81. xy = a; x2 − y2 = b, where a and b are constants
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Calculus: Early Transcendentals, Books A La Carte Edition (3rd Edition)
Additional Math Textbook Solutions
Elementary Statistics
Thinking Mathematically (6th Edition)
Pre-Algebra Student Edition
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Algebra and Trigonometry (6th Edition)
- find the zeros of the function algebraically: f(x) = 9x2 - 3x - 2arrow_forwardRylee's car is stuck in the mud. Roman and Shanice come along in a truck to help pull her out. They attach one end of a tow strap to the front of the car and the other end to the truck's trailer hitch, and the truck starts to pull. Meanwhile, Roman and Shanice get behind the car and push. The truck generates a horizontal force of 377 lb on the car. Roman and Shanice are pushing at a slight upward angle and generate a force of 119 lb on the car. These forces can be represented by vectors, as shown in the figure below. The angle between these vectors is 20.2°. Find the resultant force (the vector sum), then give its magnitude and its direction angle from the positive x-axis. 119 lb 20.2° 377 lbarrow_forwardAn airplane flies due west at an airspeed of 428 mph. The wind blows in the direction of 41° south of west at 50 mph. What is the ground speed of the airplane? What is the bearing of the airplane?arrow_forward
- A vector with magnitude 5 points in a direction 190 degrees counterclockwise from the positive x axis. Write the vector in component form, and show your answers accurate to 3 decimal places.arrow_forward||A||=23 45° Find the EXACT components of the vector above using the angle shown.arrow_forwardGiven ƒ = (10, -10) and q = (-8, −7), find ||ƒ— q|| and dƒ-9. Give EXACT answers. You do NOT have to simplify your radicals!arrow_forward
- Find a vector (u) with magnitude 7 in the direction of v = (2,4) Give EXACT answer. You do NOT have to simplify your radicals!arrow_forwardGiven g = (-5, 10) and u = (5, 2), find -4ğ - 6.arrow_forwardGiven the vector v→=⟨3,-5⟩, find the magnitude and angle in which the vector points (measured in radians counterclockwise from the positive x-axis and 0≤θ<2π). Round each decimal number to two places.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
