Bundle: Calculus: Early Transcendentals, 8th + WebAssign Printed Access Card for Stewart's Calculus: Early Transcendentals, 8th Edition, Multi-Term
8th Edition
ISBN: 9781305597624
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3.8, Problem 6E
The table gives the population of Indonesia, in millions, for the second half of the 20th century.
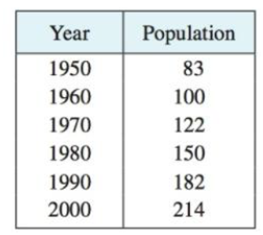
(a) Assuming the population grows at a rate proportional to its size, use the census figures for 1950 and 1960 to predict the population in 1980. Compare with the actual figure.
(b) Use the census figures for 1960 and 1980 to predict the population in 2000. Compare with the actual population.
(c) Use the census figures for 1980 and 2000 to predict the population in 2010 and compare with the actual population of 243 million.
(d) Use the model in pan (c) to predict the population in 2020. Do you think the prediction will be too high or too low? Why?
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Vo))
%TV ..
+
1
R2X2
2) slots per pole per phase = 3/31
B-180-60
msl
Kol Sin ()
Isin ()
Kd
تب بس بالفراغ
i
Cos (30) 0.866
4) Rotating
۳/۱
5) Synchronous speed; 12
S=1000-950
50
1000
Copper losses: 5kw
Rotor input 5
loo kw
0.05
6) I
العنوان
Which of the following is converge, and which diverge? Give reasons for your
answers with details. When your answer then determine the series' convergence if
possible.
اذا ميريد شرح الكتب فقط ok
7) rotor
|||
DC
11500
30tan¹()
2n=1'
m²+1
1:11
>
PV + 16°52
Which of the following is converge, and which diverge? Give reasons for your
answers with details. When your answer then determine the series' convergence if
possible.
7357
//Σm=1 (m²-5n+6)
Lake
Which of the following is converge, and which diverge? Give reasons for your
answers with details. When your answer then determine the series' convergence if
possible.
-
(3)(5+))
T
d sove in peaper
=T
M
L
ined sove in peaper
Anoting
PU+965
4
Which of the following is converge, and which diverge? Give reasons for your answers
with details. When your answer then determine the convergence sum if possible.
+1Σm=1
00
sin
Sn
Lake
55
Which of the following is converge, and which diverge? Give reasons for your answers
with details. When your answer then determine the convergence sum if possible.
5700
2n=2√2+n
C
Ministry of Higher Education &
Scientific Research
Babylon University
College of Engineering-
musayab
Homobile Department
Subject :Numerical Analyses
Stage: Third
Time: 90 min
Date: 25-4-2023
2nd month exam/2nd semester (2022-2023)
Note: Answer all questions, all questions have same degree.
Q1:Given the values
X
5
7
11
13
17
F(x)
150
392
1452
2366
5202
Evaluate f(9),using Newton's divided difference formula
Q2:A slider in a machine moves along a fixed straight rod.its distance (x cm)
along the rod is given below for various values of the time.Find the velocity
and acceleration of the slider when t=0.3 seconds.
t(seconds) 0
X (cm)
30.13
0.1
31.62
0.2 0.3 0.4 0.5 0.6
32.87 33.64 33.95 33.81 33.24
Q3:From the following table,find the area bounded by the curve and x-
axis,between the ordinates x=7.74 to x=7.52 using Simpson's 1/3 rule.
X
y=f(x)
7.47 7.48
1.93 1.95
7.49
1.98
7.50 7.51 7.52
2.01 2.03 2.06
Q4:Given
y+x
with initial condition y=1 at x=0;find (y) for x=0.1 by
Euler's method.…
Chapter 3 Solutions
Bundle: Calculus: Early Transcendentals, 8th + WebAssign Printed Access Card for Stewart's Calculus: Early Transcendentals, 8th Edition, Multi-Term
Ch. 3.1 - (a) How is the number e defined? (b) Use a...Ch. 3.1 - (a) Sketch, by hand, the graph of the function...Ch. 3.1 - Differentiate the function. f(x) = 240Ch. 3.1 - Differentiate the function. f(x) = e5Ch. 3.1 - Differentiate the function. f(x) = 5.2x + 2.3Ch. 3.1 - Differentiate the function. g(x)=74x23x+12Ch. 3.1 - Differentiate the function. f(t) = 2t3 3t2 4tCh. 3.1 - Differentiate the function. f(t) = 1.4t5 2.5t2+...Ch. 3.1 - Differentiate the function. g(x) = x2(1 2x)Ch. 3.1 - Differentiate the function. H(u) = (3u 1)(u + 2)
Ch. 3.1 - Differentiate the function. g(t) = 2t3/4Ch. 3.1 - Differentiate the function. B(y) = cy6Ch. 3.1 - Differentiate the function. F(r)=5r3Ch. 3.1 - Differentiate the function. y = x5/3 x2/3Ch. 3.1 - Differentiate the function. R(a) = (3a + 1)2Ch. 3.1 - Differentiate the function. h(t)=t44etCh. 3.1 - Differentiate the function. S(p)=ppCh. 3.1 - Differentiate the function. y=x3(2+x)Ch. 3.1 - Differentiate the function. y=3ex+4x3Ch. 3.1 - Differentiate the function. S(R) = 4R2Ch. 3.1 - Differentiate the function. h(u)=Au3+Bu2+CuCh. 3.1 - Differentiate the function. y=x+xx2Ch. 3.1 - Differentiate the function. y=x2+4x+3xCh. 3.1 - Differentiate the function. G(t)=5t+7tCh. 3.1 - Differentiate the function. j(x) = x2.4 + e2.4Ch. 3.1 - Differentiate the function. k(r) = er + reCh. 3.1 - Differentiate the function. G(q) = (1 + q1)2Ch. 3.1 - Differentiate the function. F(z)=A+Bz+Cz2z2Ch. 3.1 - Differentiate the function. f(v)=v32vevvCh. 3.1 - Differentiate the function. D(t)=1+16t2(4t)3Ch. 3.1 - Differentiate the function. z=Ay10+BeyCh. 3.1 - Differentiate the function. y = ex + 1 + 1Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find equations of the tangent line and normal line...Ch. 3.1 - Find equations of the tangent line and normal line...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find f'(x). Compare the graphs of f and f' and use...Ch. 3.1 - Find f'(x). Compare the graphs of f and f' and use...Ch. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - The equation of motion of a particle is s = t3 ...Ch. 3.1 - The equation of motion of a particle is s = t4 ...Ch. 3.1 - Biologists have proposed a cubic polynomial to...Ch. 3.1 - The number of tree species S in a given area A in...Ch. 3.1 - Boyles Law states that when a sample of gas is...Ch. 3.1 - Find the points on the curve y = 2x3 + 3x2 12x +...Ch. 3.1 - For what value of x does the graph of f(x) = ex ...Ch. 3.1 - Show that the curve y = 2ex + 3x + 5x3 has no...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find equations of both lines that are tangent to...Ch. 3.1 - At what point on the curve y = 1 + 2ex 3x is the...Ch. 3.1 - Find an equation of the normal line to the curve...Ch. 3.1 - Where does the normal line to the parabola y = x2 ...Ch. 3.1 - Draw a diagram to show that there are two tangent...Ch. 3.1 - (a) Find equations of both lines through the point...Ch. 3.1 - Use the definition of a derivative to show that if...Ch. 3.1 - Find the nth derivative of each function by...Ch. 3.1 - Find a second-degree polynomial P such that P(2) =...Ch. 3.1 - The equation y" + y' 2y = x2 is called a...Ch. 3.1 - Find a cubic function y = ax3 + bx2 + cx + d whose...Ch. 3.1 - Find a parabola with equation y = ax2 + bx + c...Ch. 3.1 - Let {x2+1ifx1x+1ifx1 Is f differentiable at 1?...Ch. 3.1 - At what numbers is the following function g...Ch. 3.1 - (a) For what values of x is the function f(x) =...Ch. 3.1 - Where is the function h(x) = |x 1| + |x + 2|...Ch. 3.1 - Find the parabola with equation y = ax2 + bx whose...Ch. 3.1 - Suppose the curve y = x4 + ax3 + bx2 + cx + d has...Ch. 3.1 - For what values of a and b is the line 2x + y = b...Ch. 3.1 - Prob. 78ECh. 3.1 - What is the value of c such that the line y = 2x +...Ch. 3.1 - The graph of any quadratic function f(x) = ax2 +...Ch. 3.1 - Let f(x){x2ifx2mx+bifx2 Find the values of m and b...Ch. 3.1 - Prob. 82ECh. 3.1 - Prob. 83ECh. 3.1 - Prob. 84ECh. 3.1 - If c12, how many lines through the point (0, c)...Ch. 3.1 - Prob. 86ECh. 3.2 - Find the derivative of f(x) = (1 + 2x2)(x x2) in...Ch. 3.2 - Find the derivative o f the function...Ch. 3.2 - Differentiate. f(x) = (3x2 5x)exCh. 3.2 - 4. Differentiate. g(x)=(x+2x)exCh. 3.2 - Differentiate. y=xexCh. 3.2 - Differentiate. y=ex1exCh. 3.2 - Differentiate. g(x)=1+2x34xCh. 3.2 - Differentiate. G(x)=x222x+1Ch. 3.2 - Differentiate. H(u)=(uu)(u+u)Ch. 3.2 - Differentiate. J(v) = (v3 2v)(v4 + v2)Ch. 3.2 - Prob. 11ECh. 3.2 - Differentiate. f(z) = (1 ez)(z + ez)Ch. 3.2 - Differentiate. y=x2+1x31Ch. 3.2 - Prob. 14ECh. 3.2 - Differentiate. y=t3+3tt24t+3Ch. 3.2 - Differentiate. y=1t3+2t21Ch. 3.2 - Differentiate. y=ep(p+pp)Ch. 3.2 - Differentiate. h(r)=aerb+erCh. 3.2 - Differentiate. y=sss2Ch. 3.2 - Prob. 20ECh. 3.2 - Differentiate. f(t)=t3t3Ch. 3.2 - Differentiate. V(t)=4+ttetCh. 3.2 - Differentiate. f(x)=x2exx2+exCh. 3.2 - Prob. 24ECh. 3.2 - Differentiate. f(x)=xx+cxCh. 3.2 - Differentiate. f(x)=ax+bcx+dCh. 3.2 - Find f'(x) and f"(x). f(x) = (x3 + 1)exCh. 3.2 - Find f'(x) and f"(x). f(x)=xexCh. 3.2 - Find f'(x) and f"(x). f(x)=x21+exCh. 3.2 - Find f'(x) and f"(x). f(x)=xx21Ch. 3.2 - Find an equation of the tangent line to the given...Ch. 3.2 - Find an equation of the tangent line to the given...Ch. 3.2 - Find equations of the tangent line and normal line...Ch. 3.2 - Find equations of the tangent line and normal line...Ch. 3.2 - (a) The curve y = 1/(1 + x2) is called a witch of...Ch. 3.2 - (a) The curve y = x/(1 + x2) is called a...Ch. 3.2 - (a) If f(x) = (x3 x)ex, find f'(x). (b) Check to...Ch. 3.2 - Prob. 38ECh. 3.2 - (a) If f(x) = (x2 1)/(x2 + 1), find f'(x) and...Ch. 3.2 - (a) If f(x) = (x2 1)ex, find f'(x) and f"(x). (b)...Ch. 3.2 - If f(x) = x2/(l + x), find f"(1).Ch. 3.2 - If g(x) = x/ex. find g(n)(x).Ch. 3.2 - Suppose that f(5) = 1, f'(5) = 6, g(5) = 3, and...Ch. 3.2 - Suppose that f(4) = 2, g(4) = 5, f'(4) = 6. and...Ch. 3.2 - If f(x) = exg(x), where g(0) = 2 and g'(0) = 5,...Ch. 3.2 - If h(2) = 4 and h'(2) = 3, find ddx(h(x)x)|x=2Ch. 3.2 - If g(x) = xf(x), where f(3) = 4 and f'(3) = 2,...Ch. 3.2 - If f(2) = 10 and f'(x) = x2f(x) for all x, find...Ch. 3.2 - If f and g are the functions whose graphs are...Ch. 3.2 - Let P(x) = F(x)G(x) and Q(x) = F(x)/G(x), where F...Ch. 3.2 - If g is a differentiable function, find an...Ch. 3.2 - If f is a differentiable function, find an...Ch. 3.2 - How many tangent lines to the curve y = x/(x + 1)...Ch. 3.2 - Find equations of the tangent lines to the curve...Ch. 3.2 - Find R'(0), where R(x)=x3x3+5x51+3x3+6x6+9x9 Hint:...Ch. 3.2 - Use the method of Exercise 55 to compute Q'(0),...Ch. 3.2 - In this exercise we estimate the rate at which the...Ch. 3.2 - A manufacturer produces bolts of a fabric with a...Ch. 3.2 - The Michaelis-Menten equation for the enzyme...Ch. 3.2 - Prob. 60ECh. 3.2 - (a) Use the Product Rule twice to prove that if f,...Ch. 3.2 - (a) If F(x) = f(x) g(x), where f and g have...Ch. 3.2 - Prob. 63ECh. 3.2 - (a) If g is differentiable, the Reciprocal Rule...Ch. 3.3 - Differentiate. f(x) = x2 sin xCh. 3.3 - Differentiate. f(x) = x cos x + 2 tan xCh. 3.3 - Differentiate. f(x) = ex cos xCh. 3.3 - Differentiate. y = 2 sec x csc xCh. 3.3 - Differentiate. y = sec tanCh. 3.3 - Differentiate. g() = e(tan )Ch. 3.3 - Differentiate. y = c cos t + t2 sin tCh. 3.3 - Differentiate. f(t)=cottetCh. 3.3 - Prob. 9ECh. 3.3 - Differentiate. y = sin cosCh. 3.3 - Differentiate f()=sin1+cosCh. 3.3 - Differentiate. y=cosx1sinxCh. 3.3 - Differentiate. y=tsint1+tCh. 3.3 - Differentiate. y=sint1+tantCh. 3.3 - Differentiate. f() = cos sinCh. 3.3 - Differentiate. f(t) = tet cot tCh. 3.3 - Prove that ddx(cscx)=cscxcotx.Ch. 3.3 - Prove that ddx(secx)=secxtanxCh. 3.3 - Prove that ddx(cotx)=csc2x.Ch. 3.3 - Prove, using the definition of derivative. that if...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - (a) Find an equation of the tangent line to the...Ch. 3.3 - Prob. 26ECh. 3.3 - (a) If f(x) = sec x x, find f'(x). (b) Check to...Ch. 3.3 - (a) If f(x) = ex cos x, find f'(x) and f"(x). (b)...Ch. 3.3 - If H() = sin , find H'() and H"( ).Ch. 3.3 - If f(t) = sec t, find f"(/4).Ch. 3.3 - (a) Use the Quotient Rule to differentiate the...Ch. 3.3 - Suppose f(/3) = 4 and f'(/3) = 2, and let g(x) =...Ch. 3.3 - For what values of x does the graph of f have a...Ch. 3.3 - For what values of x does the graph of f have a...Ch. 3.3 - A mass on a spring vibrates horizontally on a...Ch. 3.3 - An elastic band is hung on a hook and a mass is...Ch. 3.3 - A ladder 10 ft long rests against a vertical wall....Ch. 3.3 - An object with weight W is dragged along a...Ch. 3.3 - Find the limit. limx0sin5x3xCh. 3.3 - Find the limit. limx0sinxsinxCh. 3.3 - Find the limit. limt0tan6tsin2tCh. 3.3 - Prob. 42ECh. 3.3 - Find the limit. limx0sin3x5x34xCh. 3.3 - Find the limit. limx0sin3xsin5xx2Ch. 3.3 - Prob. 45ECh. 3.3 - Find the limit. limx0cscxsin(sinx)Ch. 3.3 - Prob. 47ECh. 3.3 - Find the limit. limx0sin(x2)xCh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Find constants A and B such that the function y =...Ch. 3.3 - (a) Evaluate limxxsin1x. (b) Evaluate limx0xsin1x....Ch. 3.3 - Differentiate each trigonometric identity to...Ch. 3.3 - A semicircle with diameter PQ sits on an isosceles...Ch. 3.3 - The figure shows a circular arc of length s and a...Ch. 3.3 - Prob. 58ECh. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Find the derivative of the function. F(x) = (5x6 +...Ch. 3.4 - Find the derivative of the function. F (x) = (1 +...Ch. 3.4 - Find the derivative of the function. f(x)=5x+1Ch. 3.4 - Find the derivative of the function. f(x)=1x213Ch. 3.4 - Find the derivative of the function. f() = cos(2)Ch. 3.4 - Find the derivative of the function. g() = cos2Ch. 3.4 - Find the derivative of the function. y = x2e3xCh. 3.4 - Find the derivative of the function. f(t) = t sin ...Ch. 3.4 - Find the derivative of the function. f(t) = eat...Ch. 3.4 - Find the derivative of the function. g(x)=ex2xCh. 3.4 - Find the derivative of the function. f(x) = (2x ...Ch. 3.4 - Find the derivative of the function. g(x) = (x2 +...Ch. 3.4 - Find the derivative of the function. h(t) = (t +...Ch. 3.4 - Find the derivative of the function. F(t) = (3t ...Ch. 3.4 - Find the derivative of the function. y=xx+1Ch. 3.4 - Find the derivative of the function. y=(x+1x)5Ch. 3.4 - Find the derivative of the function. y = e tanCh. 3.4 - Find the derivative of the function. f(t)2t3Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. r(t)=10t2Ch. 3.4 - Find the derivative of the function. f(z) =...Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. J() = tan2(n)Ch. 3.4 - Find the derivative of the function. F(t) = et sin...Ch. 3.4 - Find the derivative of the function. F(t)=t2t3+1Ch. 3.4 - Find the derivative of the function. G(x) = 4C/xCh. 3.4 - Prob. 34ECh. 3.4 - Find the derivative of the function....Ch. 3.4 - Prob. 36ECh. 3.4 - Find the derivative of the function. y = cot2(sin...Ch. 3.4 - Prob. 38ECh. 3.4 - Find the derivative of the function. f(t) =...Ch. 3.4 - Find the derivative of the function. y = esin 2x +...Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. y=x+x+xCh. 3.4 - Find the derivative of the function. g(x) = (2...Ch. 3.4 - Find the derivative of the function. y=234xCh. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. y = [x + (x +...Ch. 3.4 - Find y and y. y = cos(sin 3)Ch. 3.4 - Find y and y. y=1(1+tanx)2Ch. 3.4 - Find y and y. y=1sectCh. 3.4 - Find y and y. y=eexCh. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Prob. 55ECh. 3.4 - (a) The curve y=|x|/2x2 is called a bullet-nose...Ch. 3.4 - (a) If f(x)=2x2x, find f(x). (b) Check to see that...Ch. 3.4 - Prob. 58ECh. 3.4 - Find all points on the graph of the function f(x)...Ch. 3.4 - At what point on the curve y=1+2x is the tangent...Ch. 3.4 - If F(x) = f(g(x)), where f(2) = 8, f(2) = 4, f(5)...Ch. 3.4 - If h(x)=4+3f(x), where f(1) = 7andf(1) = 4, find...Ch. 3.4 - A table of values for f, g, f, and g is given. (a)...Ch. 3.4 - Prob. 64ECh. 3.4 - If f and g are the functions whose graphs are...Ch. 3.4 - If f is the function whose graph is shown, let...Ch. 3.4 - If g(x)=f(x), where the graph off is shown,...Ch. 3.4 - Prob. 68ECh. 3.4 - Suppose f is differentiable on . Let F(x) = f(ex)...Ch. 3.4 - Let g(x) = ecx + f(x) and h(x) = ekxf(x), where...Ch. 3.4 - Let r(x) = f(g(h(x))), where h(1) = 2, g(2) = 3,...Ch. 3.4 - If g is a twice differentiable function and f(x) =...Ch. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Show that the function y = e2x (A cos 3x + B sin...Ch. 3.4 - For what values of r does the function y = erx...Ch. 3.4 - Find the 50th derivative of y = cos 2x.Ch. 3.4 - Prob. 78ECh. 3.4 - The displacement of a particle on a vibrating...Ch. 3.4 - If the equation of motion of a particle is given...Ch. 3.4 - A Cepheid variable star is a star whose brightness...Ch. 3.4 - In Example 1.3.4 we arrived at a model for the...Ch. 3.4 - Prob. 83ECh. 3.4 - Under certain circumstance a rumor spreads...Ch. 3.4 - The average blood alcohol concentration (BAC) of...Ch. 3.4 - In Section 1.4 we modeled the world population...Ch. 3.4 - Prob. 87ECh. 3.4 - Air is being pumped into a spherical weather...Ch. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Use the Chain Rule to prove the following. (a) The...Ch. 3.4 - Prob. 94ECh. 3.4 - (a) If n is a positive integer, prove that...Ch. 3.4 - Prob. 96ECh. 3.4 - Use the Chain Rule to show that if is measured in...Ch. 3.4 - (a) Write |x|=x2 and use the Chain Rule to show...Ch. 3.4 - Prob. 99ECh. 3.4 - Prob. 100ECh. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - Find dy/dx by implicit differentiation. 5. x2 4xy...Ch. 3.5 - Find dy/dx by implicit differentiation. 6. 2x2 +...Ch. 3.5 - Find dy/dx by implicit differentiation. 7. x4 +...Ch. 3.5 - Find dy/dx by implicit differentiation. 8. x3 xy2...Ch. 3.5 - Find dy/dx by implicit differentiation. 9....Ch. 3.5 - Find dy/dx by implicit differentiation. 10. xey =...Ch. 3.5 - Find dy/dx by implicit differentiation. 11. y cos...Ch. 3.5 - Find dy/dx by implicit differentiation. 12....Ch. 3.5 - Find dy/dx by implicit differentiation. 13....Ch. 3.5 - Find dy/dx by implicit differentiation. 14. ey sin...Ch. 3.5 - Find dy/dx by implicit differentiation. 15. ex/y...Ch. 3.5 - Find dy/dx by implicit differentiation. 16....Ch. 3.5 - Find dy/dx by implicit differentiation. 17....Ch. 3.5 - Find dy/dx by implicit differentiation. 18. x sin...Ch. 3.5 - Find dy/dx by implicit differentiation. 19....Ch. 3.5 - Find dy/dx by implicit differentiation. 20....Ch. 3.5 - If f(x) + x2 [f(x)]3 = 10 and f(1) = 2, find f(1).Ch. 3.5 - If g(x) + x sin g(x) = x2, find g(0).Ch. 3.5 - Regard y as the independent variable and x as the...Ch. 3.5 - Regard y as the independent variable and x as the...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - (a) The curve with equation y2 = 5x4 x2 is called...Ch. 3.5 - (a) The curve with equation y2 = x3 + 3x2 is...Ch. 3.5 - Find y by implicit differentiation. 35. x2 + 4y2 =...Ch. 3.5 - Find y by implicit differentiation. 36. x2 + xy +...Ch. 3.5 - Find y by implicit differentiation. 37. sin y +...Ch. 3.5 - Find y by implicit differentiation. 38. x3 y3 = 7Ch. 3.5 - If xy + ey = e, find the value of y at the point...Ch. 3.5 - If x2 + xy + y3 = 1, find the value of y at the...Ch. 3.5 - Find the points on the lemniscate in Exercise 31...Ch. 3.5 - Show by implicit differentiation that the tangent...Ch. 3.5 - Find an equation of the tangent line to the...Ch. 3.5 - Show that the sum of the x-and y-intercepts of any...Ch. 3.5 - Show, using implicit differentiation, that any...Ch. 3.5 - The Power Rule can be proved using implicit...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 52ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 56ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 59ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find f(x). Check that your answer is reasonable by...Ch. 3.5 - Prob. 62ECh. 3.5 - Prove the formula for (d/dx)(cos1x) by the same...Ch. 3.5 - (a) One way of defining sec1x is to say that...Ch. 3.5 - Two curves are orthogonal if their tangent lines...Ch. 3.5 - Prob. 66ECh. 3.5 - Two curves are orthogonal if their tangent lines...Ch. 3.5 - Prob. 68ECh. 3.5 - Show that the ellipse x2/a2 + y2/b2 = 1 and the...Ch. 3.5 - Prob. 70ECh. 3.5 - (a) The van der Waals equation for n moles of a...Ch. 3.5 - The equation x2 xy + y2 = 3 re presents a...Ch. 3.5 - (a) Where does the normal line to the ellipse x2 ...Ch. 3.5 - Find all points on the curve x2y2 + xy = 2 where...Ch. 3.5 - Find equations of both the tangent lines to the...Ch. 3.5 - (a) Suppose f is a one-to-one differentiable...Ch. 3.5 - Prob. 78ECh. 3.5 - The Bessel function of order 0, y = J(x),...Ch. 3.5 - The figure shows a lamp located three units to the...Ch. 3.6 - Explain why the natural logarithmic function y =...Ch. 3.6 - Differentiate the function. f(x) = x ln x xCh. 3.6 - Differentiate the function. f(x ) = sin(ln x)Ch. 3.6 - Differentiate the function. f(x) = ln(sin2x)Ch. 3.6 - Differentiate the function. f(x)=ln1xCh. 3.6 - Differentiate the function. y=1lnxCh. 3.6 - Differentiate the function. f(x) = log10(1 + cos...Ch. 3.6 - Differentiate the function. f(x)log10xCh. 3.6 - Differentiate the function. g(x) = ln(xe2x)Ch. 3.6 - Differentiate the function. g(t)=1+lntCh. 3.6 - Differentiate the function. F(t) =(ln t)2 sin tCh. 3.6 - Differentiate the function. h(x)=ln(x+x21)Ch. 3.6 - Differentiate the function. G(y)=ln(2y+1)5y2+1Ch. 3.6 - Differentiate the function. p(v)=lnv1vCh. 3.6 - Differentiate the function. F(s) = ln ln sCh. 3.6 - Differentiate the function. y = ln |1 + t t3|Ch. 3.6 - Differentiate the function. T(z) = 2z log2zCh. 3.6 - Differentiate the function. y = ln(csc x cot x)Ch. 3.6 - Differentiate the function. y = ln(ex + xex)Ch. 3.6 - Differentiate the function. H(z)=a2z2a2+z2Ch. 3.6 - Differentiate the function. y = tan[ln(ax + b)]Ch. 3.6 - Differentiate the function. y = log2 (x log5 x)Ch. 3.6 - Find y and y. y=xlnxCh. 3.6 - Find y and y. y=lnx1+lnxCh. 3.6 - Find y and y. y = ln |sec x|Ch. 3.6 - Find y and y. y = ln(l + ln x)Ch. 3.6 - Differentiate f and find the domain of f....Ch. 3.6 - Differentiate f and find the domain of f....Ch. 3.6 - Differentiate f and find the domain of f. f(x) =...Ch. 3.6 - Differentiate f and find the domain of f. f(x) ln...Ch. 3.6 - If f(x) = ln(x + ln x), find f(1).Ch. 3.6 - If f(x) = cos(ln x2), find f(1).Ch. 3.6 - Find an equation of the tangent line to the curve...Ch. 3.6 - Find an equation of the tangent line to the curve...Ch. 3.6 - If f(x) = sin x + ln x, find f(x). Check that your...Ch. 3.6 - Find equations of the tangent lines to the curve y...Ch. 3.6 - Let f(x) = cx + ln(cos x). For what value of c is...Ch. 3.6 - Let f(x) = logb (3x2 2). For what value of b is...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Find y if y = ln(x2 + y2).Ch. 3.6 - Find y if xy = yx.Ch. 3.6 - Find a formula for f(n)(x) if f(x) = ln(x 1).Ch. 3.6 - Find d9dx9(x8lnx).Ch. 3.6 - Use the definition of derivative to prove that...Ch. 3.6 - Show that limn(1+xn)n=exfor any x 0.Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - Graphs of the velocity functions of two particles...Ch. 3.7 - Graphs of the position functions of two particles...Ch. 3.7 - The height (in meters) of a projectile shot...Ch. 3.7 - If a ball is thrown vertically upward with a...Ch. 3.7 - If a rock is thrown vertically upward from the...Ch. 3.7 - A particle moves with position function s = t4 ...Ch. 3.7 - (a) A company makes computer chips from square...Ch. 3.7 - (a) Sodium chlorate crystals are easy to grow in...Ch. 3.7 - (a) Find the average rate of change of the area of...Ch. 3.7 - A stone is dropped into a lake, creating a...Ch. 3.7 - A spherical balloon is being inflated. Find the...Ch. 3.7 - (a) The volume of a growing spherical cell is...Ch. 3.7 - The mass of the part of a metal rod that lies...Ch. 3.7 - If a tank holds 5000 gallons of water, which...Ch. 3.7 - The quantity of charge Q in coulombs (C) that has...Ch. 3.7 - Newtons Law of Gravitation says that the magnitude...Ch. 3.7 - Prob. 21ECh. 3.7 - Some of the highest tides in the world occur in...Ch. 3.7 - Boyles Law states that when a sample of gas is...Ch. 3.7 - If, in Example 4, one molecule of the product C is...Ch. 3.7 - In Example 6 we considered a bacteria population...Ch. 3.7 - The number of yeast cells in a laboratory culture...Ch. 3.7 - Prob. 28ECh. 3.7 - Prob. 29ECh. 3.7 - Prob. 30ECh. 3.7 - Prob. 31ECh. 3.7 - The cost function for a certain commodity is C(q)...Ch. 3.7 - Prob. 33ECh. 3.7 - If R denotes the reaction of the body to some...Ch. 3.7 - Patients undergo dialysis treatment to remove urea...Ch. 3.7 - Invasive species often display a wave of advance...Ch. 3.7 - The gas law for an ideal gas at absolute...Ch. 3.7 - In a fish farm, a population of fish is introduced...Ch. 3.7 - In the study of ecosystems, predator-prey models...Ch. 3.8 - A population of protozoa develops with a constant...Ch. 3.8 - A common inhabitant of human intestines is the...Ch. 3.8 - A bacteria culture initially contains 100 cells...Ch. 3.8 - A bacteria culture grows with constant relative...Ch. 3.8 - The table gives estimates of the world population,...Ch. 3.8 - The table gives the population of Indonesia, in...Ch. 3.8 - Experiments show that if the chemical reaction...Ch. 3.8 - Strontium-90 has a half-life of 28 days. (a) A...Ch. 3.8 - The half-life of cesium-137 is 30 years. Suppose...Ch. 3.8 - A sample oflritium-3 decayed to 94.5% of its...Ch. 3.8 - Scientists can determine the age of ancient...Ch. 3.8 - Dinosaur fossils are too old to be reliably dated...Ch. 3.8 - Prob. 13ECh. 3.8 - A curve passes through the point (0, 5) and has...Ch. 3.8 - A roast turkey is taken from an oven when its...Ch. 3.8 - In a murder investigation, the temperature of the...Ch. 3.8 - When a cold drink is taken from a refrigerator,...Ch. 3.8 - A freshly brewed cup of coffee has temperature 95C...Ch. 3.8 - Prob. 19ECh. 3.8 - (a) If 1000 is borrowed at 8% interest, find the...Ch. 3.8 - (a) If 3000 is invested at 5% interest, find the...Ch. 3.8 - (a) How long will it take an investment to double...Ch. 3.9 - Prob. 1ECh. 3.9 - (a) If A is the area of a circle with radius r and...Ch. 3.9 - Each side of a square is increasing at a rate of 6...Ch. 3.9 - The length of a rectangle is increasing at a rate...Ch. 3.9 - A cylindrical tank with radius 5 m is being filled...Ch. 3.9 - The radius of a sphere is increasing at a rate of...Ch. 3.9 - The radius of a spherical ball is increasing at a...Ch. 3.9 - The area of a triangle with sides of lengths a and...Ch. 3.9 - Suppose y=2x+1, where x and y are functions of t....Ch. 3.9 - Suppose 4x2 + 9y2 = 36, where x and y are...Ch. 3.9 - If x2 + y2 + z2 = 9, dx/dt = 5, and dy/dt = 4,...Ch. 3.9 - A particle is moving along a hyperbola xy = 8. As...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - Two cars start moving from the same point. One...Ch. 3.9 - A spotlight on the ground shines on a wall 12m...Ch. 3.9 - A man starts walking north at 4 ft/s from a point...Ch. 3.9 - A baseball diamond is a square with side 90 ft. A...Ch. 3.9 - The altitude of a triangle is increasing at a rate...Ch. 3.9 - A boat is pulled into a dock by a rope attached to...Ch. 3.9 - At noon, ship A is 100 km west of ship B. Ship A...Ch. 3.9 - Prob. 24ECh. 3.9 - Water is leaking out of an inverted conical tank...Ch. 3.9 - A trough is 10 ft long and its ends have the shape...Ch. 3.9 - A water trough is 10m long and a cross-section has...Ch. 3.9 - A swimming pool is 20 ft wide, 40 ft long, 3 ft...Ch. 3.9 - Gravel is being dumped from a conveyor belt at a...Ch. 3.9 - A kite 100ft above the ground moves horizontally...Ch. 3.9 - The sides of an equilateral triangle are...Ch. 3.9 - How fast is the angle between the ladder and the...Ch. 3.9 - The top of a ladder slides down a vertical wall at...Ch. 3.9 - According to the model we used to solve Example 2,...Ch. 3.9 - Prob. 35ECh. 3.9 - A faucet is filling a hemispherical basin of...Ch. 3.9 - Boyles Law states that when a sample of gas is...Ch. 3.9 - When air expands adiabatically (without gaining or...Ch. 3.9 - If two resistors with resistances R1 and R2 are...Ch. 3.9 - Brain weight B as a function of body weight Win...Ch. 3.9 - Two sides of a triangle have lengths 12 m and 15...Ch. 3.9 - Two carts, A and B, are connected by a rope 39 ft...Ch. 3.9 - A television camera is positioned 4000 ft from the...Ch. 3.9 - A lighthouse is located on a small island 3 km...Ch. 3.9 - A plane flies horizontally at an altitude of 5 km...Ch. 3.9 - A Ferris wheel with a radius of 10m is rotating at...Ch. 3.9 - A plane flying with a constant speed of 300 km/h...Ch. 3.9 - Two people start from the same point. One walks...Ch. 3.9 - A runner sprints around a circular track of radius...Ch. 3.9 - The minute hand on a watch is 8 mm long and the...Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linear approximation of the function...Ch. 3.10 - Find the linear approximation of the function...Ch. 3.10 - Prob. 7ECh. 3.10 - Prob. 8ECh. 3.10 - Verify the given linear approximation at a = 0....Ch. 3.10 - Prob. 10ECh. 3.10 - Find the differential of each function. 11. (a) y...Ch. 3.10 - Find the differential of each function. 12. (a)...Ch. 3.10 - Find the differential of each function. 13. (a)...Ch. 3.10 - Find the differential of each function. 14. (a) y...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - Prob. 18ECh. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Prob. 22ECh. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Prob. 32ECh. 3.10 - The edge of a cube was found to be 30 cm with a...Ch. 3.10 - The radius of a circular disk is given as 24 cm...Ch. 3.10 - The circumference of a sphere was measured to be...Ch. 3.10 - Use differentials to estimate the amount of paint...Ch. 3.10 - (a) Use differentials to find a formula for the...Ch. 3.10 - One side of a right triangle is known to be 20 cm...Ch. 3.10 - If a current I passes through a resistor with...Ch. 3.10 - When blood flows along a blood vessel, the flux F...Ch. 3.10 - Establish the following rules for working with...Ch. 3.10 - Prob. 42ECh. 3.10 - Suppose that the only information we have about a...Ch. 3.10 - Suppose that we dont have a formula for g(x) but...Ch. 3.11 - Find the numerical value of each expression. 1....Ch. 3.11 - Find the numerical value of each expression. 2....Ch. 3.11 - Find the numerical value of each expression. 3....Ch. 3.11 - Find the numerical value of each expression. 4....Ch. 3.11 - Find the numerical value of each expression. 5....Ch. 3.11 - Prob. 6ECh. 3.11 - Prove the identity. 7. sinh(x) = sinh x (This...Ch. 3.11 - Prob. 8ECh. 3.11 - Prove the identity. 9. cosh x + sinh x = exCh. 3.11 - Prove the identity. 10. cosh x sinh r = exCh. 3.11 - Prove the identity. 11. sinh(x + y) = sinh x cosh...Ch. 3.11 - Prob. 12ECh. 3.11 - Prove the identity. 13. coth2x 1 = csch2xCh. 3.11 - Prove the identity. 14....Ch. 3.11 - Prove the identity. 15. sinh 2x = 2 sinh x cosh xCh. 3.11 - Prob. 16ECh. 3.11 - Prove the identity. 17. tanh(lnx)=x21x2+1Ch. 3.11 - Prove the identity. 18. 1+tanhx1tanhx=e2xCh. 3.11 - Prove the identity. 19. (cosh x + sinh x)n = cosh...Ch. 3.11 - If x=1213 find the values of the other hyperbolic...Ch. 3.11 - If cosh=53 and x 0. find the values of the other...Ch. 3.11 - Prob. 22ECh. 3.11 - Use the definitions of the hyperbolic functions to...Ch. 3.11 - Prove the formulas given in Table 1 for the...Ch. 3.11 - Give an alternative solution 10 Example 3 by...Ch. 3.11 - Prob. 26ECh. 3.11 - Prove Equation 5 using (a) the method of Example 3...Ch. 3.11 - Prob. 28ECh. 3.11 - Prob. 29ECh. 3.11 - Find the derivative. Simplify where possible. 30....Ch. 3.11 - Find the derivative. Simplify where possible. 31....Ch. 3.11 - Find the derivative. Simplify where possible. 32....Ch. 3.11 - Find the derivative. Simplify where possible. 33....Ch. 3.11 - Prob. 34ECh. 3.11 - Find the derivative. Simplify where possible. 35....Ch. 3.11 - Find the derivative. Simplify where possible. 36....Ch. 3.11 - Find the derivative. Simplify where possible. 37....Ch. 3.11 - Prob. 38ECh. 3.11 - Find the derivative. Simplify where possible. 39....Ch. 3.11 - Prob. 40ECh. 3.11 - Find the derivative. Simplify where possible. 41....Ch. 3.11 - Find the derivative. Simplify where possible. 42....Ch. 3.11 - Find the derivative. Simplify where possible. 43....Ch. 3.11 - Prob. 44ECh. 3.11 - Prob. 45ECh. 3.11 - Prob. 46ECh. 3.11 - Prob. 47ECh. 3.11 - The Gateway Arch in St. Louis was designed by Eero...Ch. 3.11 - Prob. 49ECh. 3.11 - Prob. 50ECh. 3.11 - Prob. 51ECh. 3.11 - Prob. 52ECh. 3.11 - Prob. 53ECh. 3.11 - A model for the velocity of a falling object after...Ch. 3.11 - (a) Show that any function of the form y = A sinh...Ch. 3.11 - If x = ln( sec + tan ), show that sec = cosh x.Ch. 3.11 - At what point of the curve y = cosh x does the...Ch. 3.11 - Investigate the family of functions fn(x) = tanh...Ch. 3 - State each differentiation rule both in symbols...Ch. 3 - State the derivative of each function. (a) y = xn...Ch. 3 - (a) How is the number e defined? (b) Express e as...Ch. 3 - (a) Explain how implicit differentiation works....Ch. 3 - Give several examples of how the derivative can be...Ch. 3 - Prob. 6RCCCh. 3 - (a) Write an expression for the linearization of f...Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 10RQCh. 3 - Prob. 11RQCh. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 15RQCh. 3 - Calculate y'. 1. y = (x2 + x3)4Ch. 3 - Calculate y'. 2. y=1x1x35Ch. 3 - Prob. 3RECh. 3 - Calculate y'. 4. y=tanx1+cosxCh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Calculate y'. 8. xey = y sin xCh. 3 - Calculate y'. 9. y = ln(x ln x)Ch. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Calculate y'. 12. y = (arcsin 2x)2Ch. 3 - Prob. 13RECh. 3 - Calculate y'. 14. y = ln sec xCh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Calculate y'. 17. y=arctanCh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Calculate y'. 21. y = 3x ln xCh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Calculate y'. 24. y=1/x+x3Ch. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Calculate y'. 29. y=lnsinx12sin2xCh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Calculate y'. 33. y = ln | sec 5x + tan 5x |Ch. 3 - Prob. 34RECh. 3 - Calculate y'. 35. y = cot(3x2 + 5)Ch. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Calculate y'. 45. y = ln( cosh 3x)Ch. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Find y if x6 + y6 = 1.Ch. 3 - Find f(n)(x) if f(x) = 1/(2 x).Ch. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Find an equation of the tangent to the curve at...Ch. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Find equations of the tangent line and normal line...Ch. 3 - Find equations of the tangent line and normal line...Ch. 3 - If f(x) = xesin x find f(x). Graph f and f on the...Ch. 3 - Prob. 63RECh. 3 - (a) If f(x) = 4x tan x, /2 x /2, find f and f....Ch. 3 - At what points on the curve y = sin x + cos x, 0 ...Ch. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Suppose that f(1) = 2 f(1) = 3 f(2) = 1 f'(2) = 2...Ch. 3 - If f and g are the functions whose graphs are...Ch. 3 - Find f in terms of g. f(x) = x2g(x)Ch. 3 - Prob. 72RECh. 3 - Find f in terms of g. f(x) = [g(x)]2Ch. 3 - Prob. 74RECh. 3 - Find f in terms of g. f(x) = g(ex)Ch. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Find f in terms of g. f(x) = g(ln x)Ch. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Find f in terms of f and g. h(x) = f(g(sin 4x))Ch. 3 - Prob. 82RECh. 3 - At what point on the curve y = [ln(x + 4)]2 is the...Ch. 3 - (a) Find an equation of the tangent to the curve y...Ch. 3 - Prob. 85RECh. 3 - The function C(t) = K(eat ebt), where a, b, and K...Ch. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - A particle moves on a vertical line so that its...Ch. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - A bacteria culture contains 200 cells initially...Ch. 3 - Cobalt-60 has a half-life of 5.24 years. (a) Find...Ch. 3 - Let C(t) be the concentration of a drug in the...Ch. 3 - A cup of hot chocolate has temperature 80C in a...Ch. 3 - Prob. 97RECh. 3 - A paper cup has the shape of a cone with height 10...Ch. 3 - A balloon is rising at a constant speed of 5 ft/s....Ch. 3 - Prob. 100RECh. 3 - Prob. 101RECh. 3 - (a) Find the linear approximation to f(x)=25x2...Ch. 3 - (a) Find the linearization of f(x)1+3x3 at a = 0....Ch. 3 - Prob. 104RECh. 3 - A window has the shape of a square surmounted by a...Ch. 3 - Prob. 106RECh. 3 - Prob. 107RECh. 3 - Express the limit as a derivative and evaluate....Ch. 3 - Prob. 109RECh. 3 - Suppose f is a differentiable function such that...Ch. 3 - Prob. 111RECh. 3 - Show that the length of the portion of any tangent...Ch. 3 - Find points P and Q on the parabola y = 1 x2 so...Ch. 3 - Prob. 2PCh. 3 - Prob. 3PCh. 3 - Prob. 4PCh. 3 - If f(x)=limtxsectsecxtx, find the value of f'(/4).Ch. 3 - Find the values of the constants a and b such that...Ch. 3 - Show that sin-1(tanh x) = tan1(sinh x).Ch. 3 - Prob. 8PCh. 3 - Prove that dndxn(sin4x+cos4x)=4n1cos(4x+n/2).Ch. 3 - Prob. 10PCh. 3 - Prob. 11PCh. 3 - Find all values of r such that the parabolas y =...Ch. 3 - How many lines are tangent to both of the circles...Ch. 3 - Prob. 14PCh. 3 - The figure shows a rotating wheel with radius 40...Ch. 3 - Tangent lines T1, and T2, are drawn at two points...Ch. 3 - Prob. 17PCh. 3 - Prob. 18PCh. 3 - Prob. 19PCh. 3 - Prob. 20PCh. 3 - (a) Use the identity for tan(x y) (see Equation...Ch. 3 - Prob. 22PCh. 3 - Prob. 23PCh. 3 - Prob. 24PCh. 3 - Prob. 25PCh. 3 - For what value of k does the equation e2x=kx have...Ch. 3 - Prob. 28PCh. 3 - If y=xa212a21arctansinxa+a21+cosx show that...Ch. 3 - Given an ellipse x2/a2 + y2/b2 = 1, where a b,...Ch. 3 - Find the two points on the curve y = x4 2x2 x...Ch. 3 - Suppose that three points on the parabola y = x2...Ch. 3 - Prob. 33PCh. 3 - Prob. 34PCh. 3 - Prob. 35P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- V ined sove in peaper Pu+96er Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 21/11 55 a Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 1Σn=1 (2-") n° 3" 6"arrow_forwardL ined sove in peaper Anoting PU+965 4 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. +1Σm=1 00 sin Sn Lake 55 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 5700 2n=2√2+n Carrow_forwarda い पीर ined sove in peaper Pu+9625 Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum if possible. 3" 6" 1Σn=1 (2-") n Lake = Which of the following is converge, and which diverge? Give reasons for your answers with details. When your answer then determine the convergence sum 1/n 2" (n-√n -n 2n-1 0 T=1 . if possible.arrow_forward
- Anot ined sove in peaper +9198 PU+965 Q3// Draw and Evaluate fƒ³½³¸ x/3 x -dydx x²+y2 Lake Gart Draw and Find the centroid of the region between the parabola x + y² - 4y=0 and the 2x+y=0 in the xy-plane 3+arrow_forward: +0 العنوان I need a detailed drawing with explanation しじ ined sove in peaper Anoting Q4// Draw and Evaluate √√√xy-²sin(y²)dydx PU+96er Lake Ge Q3// Find the volume of the region between the cylinder 2 = y² and the xy- plane that is bounded by the planes x = 1, x = 2, y = -2, and y = 2. T Marrow_forwardUniversity of Babylon Faculty of Engineering-AIMusyab Automobile Eng. Dep. Year: 2022-2023, 2 Course, 1 Attempt Note: Answer five questions only. Stage Third Subject: Numerical Analysis Date: 2023\\ Time: 3 Hour Q1: Solve the poisson equation [Uxx + Uyy = -81xy), [arrow_forwardMinistry of Higher Education & Scientific Research Babylon University College of Engineering- Al musayab Subject :Numerical Analysis Stage:Third Time: 2 hour Automobile Department Date:26-3-2023 nd 1st month exam/2" semester (2022-2023) Note: Answer all questions, all questions have same degree. Q1: Use Newton's method to find solutions to the system with two step Take (X,Yo)=(8,10). { x35x2 + 2xy + 13 = 0 x3 + x²-14x-y-19=0 Q2/:Solve the system by Gauss-Seidel iterative method.(Perform only three iterations). 8x-3y+2z-20 4x+11y-z-33 6x+3y+12z-35 03/:Curve fit the data using a power function X 2 4 8 5 6 0.7500 0.1875 0.1200 0.0833 0.0469arrow_forwardUniversity of Babylon Faculty of Engineering-AlMusyab Automobile Eng. Dep. Year: 2022-2023, 2nd Course, 1 Attempt Stage: Third Subject: Numerical Analysis Date: 2023\\ Time: 3 Hour dy = x + yl Q5-A: Using Euler's method, find an approximate value of (y) corresponding to (x=0.3),given that[- and [y=1 when x=0].(taking h=0.1). dx (10 M) Q5-B Find a root of an equation[f(x)=x-x-1] using Newton Raphson method to an accuracy of &=0. (10 M) Q6:Using Newton's divided differences formula, evaluate f(8) given: X 4 58 7 103 11 13 Y=f(x) 48 100 900 294 1210 2028 (20 M) Lexaminer: Examiner: Good luck W Head of Department:arrow_forwardExplain the conditions under which the Radius of Convergence of the Power Series is a "finite positive real number" r>0arrow_forwardThis means that when the Radius of Convergence of the Power Series is a "finite positive real number" r>0, then every point x of the Power Series on (-r, r) will absolutely converge (x ∈ (-r, r)). Moreover, every point x on the Power Series (-∞, -r)U(r, +∞) will diverge (|x| >r). Please explain it.arrow_forwardExplain the conditions under which Radious of Convergence of Power Series is infinite. Explain what will happen?arrow_forwardExplain the conditions under Radius of Convergence which of Power Series is 0arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY