Bundle: Calculus: Early Transcendentals, 8th + WebAssign Printed Access Card for Stewart's Calculus: Early Transcendentals, 8th Edition, Multi-Term
Bundle: Calculus: Early Transcendentals, 8th + WebAssign Printed Access Card for Stewart's Calculus: Early Transcendentals, 8th Edition, Multi-Term
8th Edition
ISBN: 9781305597624
Author: James Stewart
Publisher: Cengage Learning
bartleby

Videos

Textbook Question
Book Icon
Chapter 3.7, Problem 3E

A particle moves according to a law of motion s = f(t), t ≥ 0, where t is measured in seconds and s in feet.

(a) Find the velocity at time t.

(b) What is the velocity after 1 second?

(c) When is the particle at rest?

(d) When is the particle moving in the positive direction?

(e) Find the total distance traveled during the first 6 seconds.

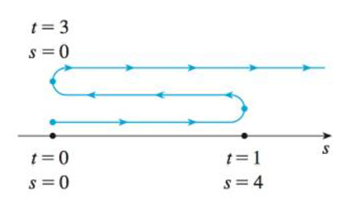
(f) Draw a diagram like Figure 2 to illustrate the motion of the particle.

(g) Find the acceleration at time t and after 1 second.

(h) Graph the position, velocity, and acceleration functions for 0 ≤ t ≤ 6.

(i) When is the particle speeding up? When is it slowing down?

FIGURE 2

Chapter 3.7, Problem 3E, A particle moves according to a law of motion s = f(t), t 0, where t is measured in seconds and s

f(t) = sin(πt/2)

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 3.7, Problem 2E
Next
Chapter 3.7, Problem 4E
Students have asked these similar questions
please do Q3
Use the properties of logarithms, given that In(2) = 0.6931 and In(3) = 1.0986, to approximate the logarithm. Use a calculator to confirm your approximations. (Round your answers to four decimal places.) (a) In(0.75) (b) In(24) (c) In(18) 1 (d) In ≈ 2 72
Find the indefinite integral. (Remember the constant of integration.) √tan(8x) tan(8x) sec²(8x) dx

Chapter 3 Solutions

Bundle: Calculus: Early Transcendentals, 8th + WebAssign Printed Access Card for Stewart's Calculus: Early Transcendentals, 8th Edition, Multi-Term

Ch. 3.1 - (a) How is the number e defined? (b) Use a...Ch. 3.1 - (a) Sketch, by hand, the graph of the function...Ch. 3.1 - Differentiate the function. f(x) = 240Ch. 3.1 - Differentiate the function. f(x) = e5Ch. 3.1 - Differentiate the function. f(x) = 5.2x + 2.3Ch. 3.1 - Differentiate the function. g(x)=74x23x+12Ch. 3.1 - Differentiate the function. f(t) = 2t3 3t2 4tCh. 3.1 - Differentiate the function. f(t) = 1.4t5 2.5t2+...Ch. 3.1 - Differentiate the function. g(x) = x2(1 2x)Ch. 3.1 - Differentiate the function. H(u) = (3u 1)(u + 2)
Ch. 3.1 - Differentiate the function. g(t) = 2t3/4Ch. 3.1 - Differentiate the function. B(y) = cy6Ch. 3.1 - Differentiate the function. F(r)=5r3Ch. 3.1 - Differentiate the function. y = x5/3 x2/3Ch. 3.1 - Differentiate the function. R(a) = (3a + 1)2Ch. 3.1 - Differentiate the function. h(t)=t44etCh. 3.1 - Differentiate the function. S(p)=ppCh. 3.1 - Differentiate the function. y=x3(2+x)Ch. 3.1 - Differentiate the function. y=3ex+4x3Ch. 3.1 - Differentiate the function. S(R) = 4R2Ch. 3.1 - Differentiate the function. h(u)=Au3+Bu2+CuCh. 3.1 - Differentiate the function. y=x+xx2Ch. 3.1 - Differentiate the function. y=x2+4x+3xCh. 3.1 - Differentiate the function. G(t)=5t+7tCh. 3.1 - Differentiate the function. j(x) = x2.4 + e2.4Ch. 3.1 - Differentiate the function. k(r) = er + reCh. 3.1 - Differentiate the function. G(q) = (1 + q1)2Ch. 3.1 - Differentiate the function. F(z)=A+Bz+Cz2z2Ch. 3.1 - Differentiate the function. f(v)=v32vevvCh. 3.1 - Differentiate the function. D(t)=1+16t2(4t)3Ch. 3.1 - Differentiate the function. z=Ay10+BeyCh. 3.1 - Differentiate the function. y = ex + 1 + 1Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find equations of the tangent line and normal line...Ch. 3.1 - Find equations of the tangent line and normal line...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find f'(x). Compare the graphs of f and f' and use...Ch. 3.1 - Find f'(x). Compare the graphs of f and f' and use...Ch. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - The equation of motion of a particle is s = t3 ...Ch. 3.1 - The equation of motion of a particle is s = t4 ...Ch. 3.1 - Biologists have proposed a cubic polynomial to...Ch. 3.1 - The number of tree species S in a given area A in...Ch. 3.1 - Boyles Law states that when a sample of gas is...Ch. 3.1 - Find the points on the curve y = 2x3 + 3x2 12x +...Ch. 3.1 - For what value of x does the graph of f(x) = ex ...Ch. 3.1 - Show that the curve y = 2ex + 3x + 5x3 has no...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find equations of both lines that are tangent to...Ch. 3.1 - At what point on the curve y = 1 + 2ex 3x is the...Ch. 3.1 - Find an equation of the normal line to the curve...Ch. 3.1 - Where does the normal line to the parabola y = x2 ...Ch. 3.1 - Draw a diagram to show that there are two tangent...Ch. 3.1 - (a) Find equations of both lines through the point...Ch. 3.1 - Use the definition of a derivative to show that if...Ch. 3.1 - Find the nth derivative of each function by...Ch. 3.1 - Find a second-degree polynomial P such that P(2) =...Ch. 3.1 - The equation y" + y' 2y = x2 is called a...Ch. 3.1 - Find a cubic function y = ax3 + bx2 + cx + d whose...Ch. 3.1 - Find a parabola with equation y = ax2 + bx + c...Ch. 3.1 - Let {x2+1ifx1x+1ifx1 Is f differentiable at 1?...Ch. 3.1 - At what numbers is the following function g...Ch. 3.1 - (a) For what values of x is the function f(x) =...Ch. 3.1 - Where is the function h(x) = |x 1| + |x + 2|...Ch. 3.1 - Find the parabola with equation y = ax2 + bx whose...Ch. 3.1 - Suppose the curve y = x4 + ax3 + bx2 + cx + d has...Ch. 3.1 - For what values of a and b is the line 2x + y = b...Ch. 3.1 - Prob. 78ECh. 3.1 - What is the value of c such that the line y = 2x +...Ch. 3.1 - The graph of any quadratic function f(x) = ax2 +...Ch. 3.1 - Let f(x){x2ifx2mx+bifx2 Find the values of m and b...Ch. 3.1 - Prob. 82ECh. 3.1 - Prob. 83ECh. 3.1 - Prob. 84ECh. 3.1 - If c12, how many lines through the point (0, c)...Ch. 3.1 - Prob. 86ECh. 3.2 - Find the derivative of f(x) = (1 + 2x2)(x x2) in...Ch. 3.2 - Find the derivative o f the function...Ch. 3.2 - Differentiate. f(x) = (3x2 5x)exCh. 3.2 - 4. Differentiate. g(x)=(x+2x)exCh. 3.2 - Differentiate. y=xexCh. 3.2 - Differentiate. y=ex1exCh. 3.2 - Differentiate. g(x)=1+2x34xCh. 3.2 - Differentiate. G(x)=x222x+1Ch. 3.2 - Differentiate. H(u)=(uu)(u+u)Ch. 3.2 - Differentiate. J(v) = (v3 2v)(v4 + v2)Ch. 3.2 - Prob. 11ECh. 3.2 - Differentiate. f(z) = (1 ez)(z + ez)Ch. 3.2 - Differentiate. y=x2+1x31Ch. 3.2 - Prob. 14ECh. 3.2 - Differentiate. y=t3+3tt24t+3Ch. 3.2 - Differentiate. y=1t3+2t21Ch. 3.2 - Differentiate. y=ep(p+pp)Ch. 3.2 - Differentiate. h(r)=aerb+erCh. 3.2 - Differentiate. y=sss2Ch. 3.2 - Prob. 20ECh. 3.2 - Differentiate. f(t)=t3t3Ch. 3.2 - Differentiate. V(t)=4+ttetCh. 3.2 - Differentiate. f(x)=x2exx2+exCh. 3.2 - Prob. 24ECh. 3.2 - Differentiate. f(x)=xx+cxCh. 3.2 - Differentiate. f(x)=ax+bcx+dCh. 3.2 - Find f'(x) and f"(x). f(x) = (x3 + 1)exCh. 3.2 - Find f'(x) and f"(x). f(x)=xexCh. 3.2 - Find f'(x) and f"(x). f(x)=x21+exCh. 3.2 - Find f'(x) and f"(x). f(x)=xx21Ch. 3.2 - Find an equation of the tangent line to the given...Ch. 3.2 - Find an equation of the tangent line to the given...Ch. 3.2 - Find equations of the tangent line and normal line...Ch. 3.2 - Find equations of the tangent line and normal line...Ch. 3.2 - (a) The curve y = 1/(1 + x2) is called a witch of...Ch. 3.2 - (a) The curve y = x/(1 + x2) is called a...Ch. 3.2 - (a) If f(x) = (x3 x)ex, find f'(x). (b) Check to...Ch. 3.2 - Prob. 38ECh. 3.2 - (a) If f(x) = (x2 1)/(x2 + 1), find f'(x) and...Ch. 3.2 - (a) If f(x) = (x2 1)ex, find f'(x) and f"(x). (b)...Ch. 3.2 - If f(x) = x2/(l + x), find f"(1).Ch. 3.2 - If g(x) = x/ex. find g(n)(x).Ch. 3.2 - Suppose that f(5) = 1, f'(5) = 6, g(5) = 3, and...Ch. 3.2 - Suppose that f(4) = 2, g(4) = 5, f'(4) = 6. and...Ch. 3.2 - If f(x) = exg(x), where g(0) = 2 and g'(0) = 5,...Ch. 3.2 - If h(2) = 4 and h'(2) = 3, find ddx(h(x)x)|x=2Ch. 3.2 - If g(x) = xf(x), where f(3) = 4 and f'(3) = 2,...Ch. 3.2 - If f(2) = 10 and f'(x) = x2f(x) for all x, find...Ch. 3.2 - If f and g are the functions whose graphs are...Ch. 3.2 - Let P(x) = F(x)G(x) and Q(x) = F(x)/G(x), where F...Ch. 3.2 - If g is a differentiable function, find an...Ch. 3.2 - If f is a differentiable function, find an...Ch. 3.2 - How many tangent lines to the curve y = x/(x + 1)...Ch. 3.2 - Find equations of the tangent lines to the curve...Ch. 3.2 - Find R'(0), where R(x)=x3x3+5x51+3x3+6x6+9x9 Hint:...Ch. 3.2 - Use the method of Exercise 55 to compute Q'(0),...Ch. 3.2 - In this exercise we estimate the rate at which the...Ch. 3.2 - A manufacturer produces bolts of a fabric with a...Ch. 3.2 - The Michaelis-Menten equation for the enzyme...Ch. 3.2 - Prob. 60ECh. 3.2 - (a) Use the Product Rule twice to prove that if f,...Ch. 3.2 - (a) If F(x) = f(x) g(x), where f and g have...Ch. 3.2 - Prob. 63ECh. 3.2 - (a) If g is differentiable, the Reciprocal Rule...Ch. 3.3 - Differentiate. f(x) = x2 sin xCh. 3.3 - Differentiate. f(x) = x cos x + 2 tan xCh. 3.3 - Differentiate. f(x) = ex cos xCh. 3.3 - Differentiate. y = 2 sec x csc xCh. 3.3 - Differentiate. y = sec tanCh. 3.3 - Differentiate. g() = e(tan )Ch. 3.3 - Differentiate. y = c cos t + t2 sin tCh. 3.3 - Differentiate. f(t)=cottetCh. 3.3 - Prob. 9ECh. 3.3 - Differentiate. y = sin cosCh. 3.3 - Differentiate f()=sin1+cosCh. 3.3 - Differentiate. y=cosx1sinxCh. 3.3 - Differentiate. y=tsint1+tCh. 3.3 - Differentiate. y=sint1+tantCh. 3.3 - Differentiate. f() = cos sinCh. 3.3 - Differentiate. f(t) = tet cot tCh. 3.3 - Prove that ddx(cscx)=cscxcotx.Ch. 3.3 - Prove that ddx(secx)=secxtanxCh. 3.3 - Prove that ddx(cotx)=csc2x.Ch. 3.3 - Prove, using the definition of derivative. that if...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - (a) Find an equation of the tangent line to the...Ch. 3.3 - Prob. 26ECh. 3.3 - (a) If f(x) = sec x x, find f'(x). (b) Check to...Ch. 3.3 - (a) If f(x) = ex cos x, find f'(x) and f"(x). (b)...Ch. 3.3 - If H() = sin , find H'() and H"( ).Ch. 3.3 - If f(t) = sec t, find f"(/4).Ch. 3.3 - (a) Use the Quotient Rule to differentiate the...Ch. 3.3 - Suppose f(/3) = 4 and f'(/3) = 2, and let g(x) =...Ch. 3.3 - For what values of x does the graph of f have a...Ch. 3.3 - For what values of x does the graph of f have a...Ch. 3.3 - A mass on a spring vibrates horizontally on a...Ch. 3.3 - An elastic band is hung on a hook and a mass is...Ch. 3.3 - A ladder 10 ft long rests against a vertical wall....Ch. 3.3 - An object with weight W is dragged along a...Ch. 3.3 - Find the limit. limx0sin5x3xCh. 3.3 - Find the limit. limx0sinxsinxCh. 3.3 - Find the limit. limt0tan6tsin2tCh. 3.3 - Prob. 42ECh. 3.3 - Find the limit. limx0sin3x5x34xCh. 3.3 - Find the limit. limx0sin3xsin5xx2Ch. 3.3 - Prob. 45ECh. 3.3 - Find the limit. limx0cscxsin(sinx)Ch. 3.3 - Prob. 47ECh. 3.3 - Find the limit. limx0sin(x2)xCh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Find constants A and B such that the function y =...Ch. 3.3 - (a) Evaluate limxxsin1x. (b) Evaluate limx0xsin1x....Ch. 3.3 - Differentiate each trigonometric identity to...Ch. 3.3 - A semicircle with diameter PQ sits on an isosceles...Ch. 3.3 - The figure shows a circular arc of length s and a...Ch. 3.3 - Prob. 58ECh. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Find the derivative of the function. F(x) = (5x6 +...Ch. 3.4 - Find the derivative of the function. F (x) = (1 +...Ch. 3.4 - Find the derivative of the function. f(x)=5x+1Ch. 3.4 - Find the derivative of the function. f(x)=1x213Ch. 3.4 - Find the derivative of the function. f() = cos(2)Ch. 3.4 - Find the derivative of the function. g() = cos2Ch. 3.4 - Find the derivative of the function. y = x2e3xCh. 3.4 - Find the derivative of the function. f(t) = t sin ...Ch. 3.4 - Find the derivative of the function. f(t) = eat...Ch. 3.4 - Find the derivative of the function. g(x)=ex2xCh. 3.4 - Find the derivative of the function. f(x) = (2x ...Ch. 3.4 - Find the derivative of the function. g(x) = (x2 +...Ch. 3.4 - Find the derivative of the function. h(t) = (t +...Ch. 3.4 - Find the derivative of the function. F(t) = (3t ...Ch. 3.4 - Find the derivative of the function. y=xx+1Ch. 3.4 - Find the derivative of the function. y=(x+1x)5Ch. 3.4 - Find the derivative of the function. y = e tanCh. 3.4 - Find the derivative of the function. f(t)2t3Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. r(t)=10t2Ch. 3.4 - Find the derivative of the function. f(z) =...Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. J() = tan2(n)Ch. 3.4 - Find the derivative of the function. F(t) = et sin...Ch. 3.4 - Find the derivative of the function. F(t)=t2t3+1Ch. 3.4 - Find the derivative of the function. G(x) = 4C/xCh. 3.4 - Prob. 34ECh. 3.4 - Find the derivative of the function....Ch. 3.4 - Prob. 36ECh. 3.4 - Find the derivative of the function. y = cot2(sin...Ch. 3.4 - Prob. 38ECh. 3.4 - Find the derivative of the function. f(t) =...Ch. 3.4 - Find the derivative of the function. y = esin 2x +...Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. y=x+x+xCh. 3.4 - Find the derivative of the function. g(x) = (2...Ch. 3.4 - Find the derivative of the function. y=234xCh. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. y = [x + (x +...Ch. 3.4 - Find y and y. y = cos(sin 3)Ch. 3.4 - Find y and y. y=1(1+tanx)2Ch. 3.4 - Find y and y. y=1sectCh. 3.4 - Find y and y. y=eexCh. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Prob. 55ECh. 3.4 - (a) The curve y=|x|/2x2 is called a bullet-nose...Ch. 3.4 - (a) If f(x)=2x2x, find f(x). (b) Check to see that...Ch. 3.4 - Prob. 58ECh. 3.4 - Find all points on the graph of the function f(x)...Ch. 3.4 - At what point on the curve y=1+2x is the tangent...Ch. 3.4 - If F(x) = f(g(x)), where f(2) = 8, f(2) = 4, f(5)...Ch. 3.4 - If h(x)=4+3f(x), where f(1) = 7andf(1) = 4, find...Ch. 3.4 - A table of values for f, g, f, and g is given. (a)...Ch. 3.4 - Prob. 64ECh. 3.4 - If f and g are the functions whose graphs are...Ch. 3.4 - If f is the function whose graph is shown, let...Ch. 3.4 - If g(x)=f(x), where the graph off is shown,...Ch. 3.4 - Prob. 68ECh. 3.4 - Suppose f is differentiable on . Let F(x) = f(ex)...Ch. 3.4 - Let g(x) = ecx + f(x) and h(x) = ekxf(x), where...Ch. 3.4 - Let r(x) = f(g(h(x))), where h(1) = 2, g(2) = 3,...Ch. 3.4 - If g is a twice differentiable function and f(x) =...Ch. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Show that the function y = e2x (A cos 3x + B sin...Ch. 3.4 - For what values of r does the function y = erx...Ch. 3.4 - Find the 50th derivative of y = cos 2x.Ch. 3.4 - Prob. 78ECh. 3.4 - The displacement of a particle on a vibrating...Ch. 3.4 - If the equation of motion of a particle is given...Ch. 3.4 - A Cepheid variable star is a star whose brightness...Ch. 3.4 - In Example 1.3.4 we arrived at a model for the...Ch. 3.4 - Prob. 83ECh. 3.4 - Under certain circumstance a rumor spreads...Ch. 3.4 - The average blood alcohol concentration (BAC) of...Ch. 3.4 - In Section 1.4 we modeled the world population...Ch. 3.4 - Prob. 87ECh. 3.4 - Air is being pumped into a spherical weather...Ch. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Use the Chain Rule to prove the following. (a) The...Ch. 3.4 - Prob. 94ECh. 3.4 - (a) If n is a positive integer, prove that...Ch. 3.4 - Prob. 96ECh. 3.4 - Use the Chain Rule to show that if is measured in...Ch. 3.4 - (a) Write |x|=x2 and use the Chain Rule to show...Ch. 3.4 - Prob. 99ECh. 3.4 - Prob. 100ECh. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - Find dy/dx by implicit differentiation. 5. x2 4xy...Ch. 3.5 - Find dy/dx by implicit differentiation. 6. 2x2 +...Ch. 3.5 - Find dy/dx by implicit differentiation. 7. x4 +...Ch. 3.5 - Find dy/dx by implicit differentiation. 8. x3 xy2...Ch. 3.5 - Find dy/dx by implicit differentiation. 9....Ch. 3.5 - Find dy/dx by implicit differentiation. 10. xey =...Ch. 3.5 - Find dy/dx by implicit differentiation. 11. y cos...Ch. 3.5 - Find dy/dx by implicit differentiation. 12....Ch. 3.5 - Find dy/dx by implicit differentiation. 13....Ch. 3.5 - Find dy/dx by implicit differentiation. 14. ey sin...Ch. 3.5 - Find dy/dx by implicit differentiation. 15. ex/y...Ch. 3.5 - Find dy/dx by implicit differentiation. 16....Ch. 3.5 - Find dy/dx by implicit differentiation. 17....Ch. 3.5 - Find dy/dx by implicit differentiation. 18. x sin...Ch. 3.5 - Find dy/dx by implicit differentiation. 19....Ch. 3.5 - Find dy/dx by implicit differentiation. 20....Ch. 3.5 - If f(x) + x2 [f(x)]3 = 10 and f(1) = 2, find f(1).Ch. 3.5 - If g(x) + x sin g(x) = x2, find g(0).Ch. 3.5 - Regard y as the independent variable and x as the...Ch. 3.5 - Regard y as the independent variable and x as the...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - (a) The curve with equation y2 = 5x4 x2 is called...Ch. 3.5 - (a) The curve with equation y2 = x3 + 3x2 is...Ch. 3.5 - Find y by implicit differentiation. 35. x2 + 4y2 =...Ch. 3.5 - Find y by implicit differentiation. 36. x2 + xy +...Ch. 3.5 - Find y by implicit differentiation. 37. sin y +...Ch. 3.5 - Find y by implicit differentiation. 38. x3 y3 = 7Ch. 3.5 - If xy + ey = e, find the value of y at the point...Ch. 3.5 - If x2 + xy + y3 = 1, find the value of y at the...Ch. 3.5 - Find the points on the lemniscate in Exercise 31...Ch. 3.5 - Show by implicit differentiation that the tangent...Ch. 3.5 - Find an equation of the tangent line to the...Ch. 3.5 - Show that the sum of the x-and y-intercepts of any...Ch. 3.5 - Show, using implicit differentiation, that any...Ch. 3.5 - The Power Rule can be proved using implicit...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 52ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 56ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 59ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find f(x). Check that your answer is reasonable by...Ch. 3.5 - Prob. 62ECh. 3.5 - Prove the formula for (d/dx)(cos1x) by the same...Ch. 3.5 - (a) One way of defining sec1x is to say that...Ch. 3.5 - Two curves are orthogonal if their tangent lines...Ch. 3.5 - Prob. 66ECh. 3.5 - Two curves are orthogonal if their tangent lines...Ch. 3.5 - Prob. 68ECh. 3.5 - Show that the ellipse x2/a2 + y2/b2 = 1 and the...Ch. 3.5 - Prob. 70ECh. 3.5 - (a) The van der Waals equation for n moles of a...Ch. 3.5 - The equation x2 xy + y2 = 3 re presents a...Ch. 3.5 - (a) Where does the normal line to the ellipse x2 ...Ch. 3.5 - Find all points on the curve x2y2 + xy = 2 where...Ch. 3.5 - Find equations of both the tangent lines to the...Ch. 3.5 - (a) Suppose f is a one-to-one differentiable...Ch. 3.5 - Prob. 78ECh. 3.5 - The Bessel function of order 0, y = J(x),...Ch. 3.5 - The figure shows a lamp located three units to the...Ch. 3.6 - Explain why the natural logarithmic function y =...Ch. 3.6 - Differentiate the function. f(x) = x ln x xCh. 3.6 - Differentiate the function. f(x ) = sin(ln x)Ch. 3.6 - Differentiate the function. f(x) = ln(sin2x)Ch. 3.6 - Differentiate the function. f(x)=ln1xCh. 3.6 - Differentiate the function. y=1lnxCh. 3.6 - Differentiate the function. f(x) = log10(1 + cos...Ch. 3.6 - Differentiate the function. f(x)log10xCh. 3.6 - Differentiate the function. g(x) = ln(xe2x)Ch. 3.6 - Differentiate the function. g(t)=1+lntCh. 3.6 - Differentiate the function. F(t) =(ln t)2 sin tCh. 3.6 - Differentiate the function. h(x)=ln(x+x21)Ch. 3.6 - Differentiate the function. G(y)=ln(2y+1)5y2+1Ch. 3.6 - Differentiate the function. p(v)=lnv1vCh. 3.6 - Differentiate the function. F(s) = ln ln sCh. 3.6 - Differentiate the function. y = ln |1 + t t3|Ch. 3.6 - Differentiate the function. T(z) = 2z log2zCh. 3.6 - Differentiate the function. y = ln(csc x cot x)Ch. 3.6 - Differentiate the function. y = ln(ex + xex)Ch. 3.6 - Differentiate the function. H(z)=a2z2a2+z2Ch. 3.6 - Differentiate the function. y = tan[ln(ax + b)]Ch. 3.6 - Differentiate the function. y = log2 (x log5 x)Ch. 3.6 - Find y and y. y=xlnxCh. 3.6 - Find y and y. y=lnx1+lnxCh. 3.6 - Find y and y. y = ln |sec x|Ch. 3.6 - Find y and y. y = ln(l + ln x)Ch. 3.6 - Differentiate f and find the domain of f....Ch. 3.6 - Differentiate f and find the domain of f....Ch. 3.6 - Differentiate f and find the domain of f. f(x) =...Ch. 3.6 - Differentiate f and find the domain of f. f(x) ln...Ch. 3.6 - If f(x) = ln(x + ln x), find f(1).Ch. 3.6 - If f(x) = cos(ln x2), find f(1).Ch. 3.6 - Find an equation of the tangent line to the curve...Ch. 3.6 - Find an equation of the tangent line to the curve...Ch. 3.6 - If f(x) = sin x + ln x, find f(x). Check that your...Ch. 3.6 - Find equations of the tangent lines to the curve y...Ch. 3.6 - Let f(x) = cx + ln(cos x). For what value of c is...Ch. 3.6 - Let f(x) = logb (3x2 2). For what value of b is...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Find y if y = ln(x2 + y2).Ch. 3.6 - Find y if xy = yx.Ch. 3.6 - Find a formula for f(n)(x) if f(x) = ln(x 1).Ch. 3.6 - Find d9dx9(x8lnx).Ch. 3.6 - Use the definition of derivative to prove that...Ch. 3.6 - Show that limn(1+xn)n=exfor any x 0.Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - Graphs of the velocity functions of two particles...Ch. 3.7 - Graphs of the position functions of two particles...Ch. 3.7 - The height (in meters) of a projectile shot...Ch. 3.7 - If a ball is thrown vertically upward with a...Ch. 3.7 - If a rock is thrown vertically upward from the...Ch. 3.7 - A particle moves with position function s = t4 ...Ch. 3.7 - (a) A company makes computer chips from square...Ch. 3.7 - (a) Sodium chlorate crystals are easy to grow in...Ch. 3.7 - (a) Find the average rate of change of the area of...Ch. 3.7 - A stone is dropped into a lake, creating a...Ch. 3.7 - A spherical balloon is being inflated. Find the...Ch. 3.7 - (a) The volume of a growing spherical cell is...Ch. 3.7 - The mass of the part of a metal rod that lies...Ch. 3.7 - If a tank holds 5000 gallons of water, which...Ch. 3.7 - The quantity of charge Q in coulombs (C) that has...Ch. 3.7 - Newtons Law of Gravitation says that the magnitude...Ch. 3.7 - Prob. 21ECh. 3.7 - Some of the highest tides in the world occur in...Ch. 3.7 - Boyles Law states that when a sample of gas is...Ch. 3.7 - If, in Example 4, one molecule of the product C is...Ch. 3.7 - In Example 6 we considered a bacteria population...Ch. 3.7 - The number of yeast cells in a laboratory culture...Ch. 3.7 - Prob. 28ECh. 3.7 - Prob. 29ECh. 3.7 - Prob. 30ECh. 3.7 - Prob. 31ECh. 3.7 - The cost function for a certain commodity is C(q)...Ch. 3.7 - Prob. 33ECh. 3.7 - If R denotes the reaction of the body to some...Ch. 3.7 - Patients undergo dialysis treatment to remove urea...Ch. 3.7 - Invasive species often display a wave of advance...Ch. 3.7 - The gas law for an ideal gas at absolute...Ch. 3.7 - In a fish farm, a population of fish is introduced...Ch. 3.7 - In the study of ecosystems, predator-prey models...Ch. 3.8 - A population of protozoa develops with a constant...Ch. 3.8 - A common inhabitant of human intestines is the...Ch. 3.8 - A bacteria culture initially contains 100 cells...Ch. 3.8 - A bacteria culture grows with constant relative...Ch. 3.8 - The table gives estimates of the world population,...Ch. 3.8 - The table gives the population of Indonesia, in...Ch. 3.8 - Experiments show that if the chemical reaction...Ch. 3.8 - Strontium-90 has a half-life of 28 days. (a) A...Ch. 3.8 - The half-life of cesium-137 is 30 years. Suppose...Ch. 3.8 - A sample oflritium-3 decayed to 94.5% of its...Ch. 3.8 - Scientists can determine the age of ancient...Ch. 3.8 - Dinosaur fossils are too old to be reliably dated...Ch. 3.8 - Prob. 13ECh. 3.8 - A curve passes through the point (0, 5) and has...Ch. 3.8 - A roast turkey is taken from an oven when its...Ch. 3.8 - In a murder investigation, the temperature of the...Ch. 3.8 - When a cold drink is taken from a refrigerator,...Ch. 3.8 - A freshly brewed cup of coffee has temperature 95C...Ch. 3.8 - Prob. 19ECh. 3.8 - (a) If 1000 is borrowed at 8% interest, find the...Ch. 3.8 - (a) If 3000 is invested at 5% interest, find the...Ch. 3.8 - (a) How long will it take an investment to double...Ch. 3.9 - Prob. 1ECh. 3.9 - (a) If A is the area of a circle with radius r and...Ch. 3.9 - Each side of a square is increasing at a rate of 6...Ch. 3.9 - The length of a rectangle is increasing at a rate...Ch. 3.9 - A cylindrical tank with radius 5 m is being filled...Ch. 3.9 - The radius of a sphere is increasing at a rate of...Ch. 3.9 - The radius of a spherical ball is increasing at a...Ch. 3.9 - The area of a triangle with sides of lengths a and...Ch. 3.9 - Suppose y=2x+1, where x and y are functions of t....Ch. 3.9 - Suppose 4x2 + 9y2 = 36, where x and y are...Ch. 3.9 - If x2 + y2 + z2 = 9, dx/dt = 5, and dy/dt = 4,...Ch. 3.9 - A particle is moving along a hyperbola xy = 8. As...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - Two cars start moving from the same point. One...Ch. 3.9 - A spotlight on the ground shines on a wall 12m...Ch. 3.9 - A man starts walking north at 4 ft/s from a point...Ch. 3.9 - A baseball diamond is a square with side 90 ft. A...Ch. 3.9 - The altitude of a triangle is increasing at a rate...Ch. 3.9 - A boat is pulled into a dock by a rope attached to...Ch. 3.9 - At noon, ship A is 100 km west of ship B. Ship A...Ch. 3.9 - Prob. 24ECh. 3.9 - Water is leaking out of an inverted conical tank...Ch. 3.9 - A trough is 10 ft long and its ends have the shape...Ch. 3.9 - A water trough is 10m long and a cross-section has...Ch. 3.9 - A swimming pool is 20 ft wide, 40 ft long, 3 ft...Ch. 3.9 - Gravel is being dumped from a conveyor belt at a...Ch. 3.9 - A kite 100ft above the ground moves horizontally...Ch. 3.9 - The sides of an equilateral triangle are...Ch. 3.9 - How fast is the angle between the ladder and the...Ch. 3.9 - The top of a ladder slides down a vertical wall at...Ch. 3.9 - According to the model we used to solve Example 2,...Ch. 3.9 - Prob. 35ECh. 3.9 - A faucet is filling a hemispherical basin of...Ch. 3.9 - Boyles Law states that when a sample of gas is...Ch. 3.9 - When air expands adiabatically (without gaining or...Ch. 3.9 - If two resistors with resistances R1 and R2 are...Ch. 3.9 - Brain weight B as a function of body weight Win...Ch. 3.9 - Two sides of a triangle have lengths 12 m and 15...Ch. 3.9 - Two carts, A and B, are connected by a rope 39 ft...Ch. 3.9 - A television camera is positioned 4000 ft from the...Ch. 3.9 - A lighthouse is located on a small island 3 km...Ch. 3.9 - A plane flies horizontally at an altitude of 5 km...Ch. 3.9 - A Ferris wheel with a radius of 10m is rotating at...Ch. 3.9 - A plane flying with a constant speed of 300 km/h...Ch. 3.9 - Two people start from the same point. One walks...Ch. 3.9 - A runner sprints around a circular track of radius...Ch. 3.9 - The minute hand on a watch is 8 mm long and the...Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linear approximation of the function...Ch. 3.10 - Find the linear approximation of the function...Ch. 3.10 - Prob. 7ECh. 3.10 - Prob. 8ECh. 3.10 - Verify the given linear approximation at a = 0....Ch. 3.10 - Prob. 10ECh. 3.10 - Find the differential of each function. 11. (a) y...Ch. 3.10 - Find the differential of each function. 12. (a)...Ch. 3.10 - Find the differential of each function. 13. (a)...Ch. 3.10 - Find the differential of each function. 14. (a) y...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - Prob. 18ECh. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Prob. 22ECh. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Prob. 32ECh. 3.10 - The edge of a cube was found to be 30 cm with a...Ch. 3.10 - The radius of a circular disk is given as 24 cm...Ch. 3.10 - The circumference of a sphere was measured to be...Ch. 3.10 - Use differentials to estimate the amount of paint...Ch. 3.10 - (a) Use differentials to find a formula for the...Ch. 3.10 - One side of a right triangle is known to be 20 cm...Ch. 3.10 - If a current I passes through a resistor with...Ch. 3.10 - When blood flows along a blood vessel, the flux F...Ch. 3.10 - Establish the following rules for working with...Ch. 3.10 - Prob. 42ECh. 3.10 - Suppose that the only information we have about a...Ch. 3.10 - Suppose that we dont have a formula for g(x) but...Ch. 3.11 - Find the numerical value of each expression. 1....Ch. 3.11 - Find the numerical value of each expression. 2....Ch. 3.11 - Find the numerical value of each expression. 3....Ch. 3.11 - Find the numerical value of each expression. 4....Ch. 3.11 - Find the numerical value of each expression. 5....Ch. 3.11 - Prob. 6ECh. 3.11 - Prove the identity. 7. sinh(x) = sinh x (This...Ch. 3.11 - Prob. 8ECh. 3.11 - Prove the identity. 9. cosh x + sinh x = exCh. 3.11 - Prove the identity. 10. cosh x sinh r = exCh. 3.11 - Prove the identity. 11. sinh(x + y) = sinh x cosh...Ch. 3.11 - Prob. 12ECh. 3.11 - Prove the identity. 13. coth2x 1 = csch2xCh. 3.11 - Prove the identity. 14....Ch. 3.11 - Prove the identity. 15. sinh 2x = 2 sinh x cosh xCh. 3.11 - Prob. 16ECh. 3.11 - Prove the identity. 17. tanh(lnx)=x21x2+1Ch. 3.11 - Prove the identity. 18. 1+tanhx1tanhx=e2xCh. 3.11 - Prove the identity. 19. (cosh x + sinh x)n = cosh...Ch. 3.11 - If x=1213 find the values of the other hyperbolic...Ch. 3.11 - If cosh=53 and x 0. find the values of the other...Ch. 3.11 - Prob. 22ECh. 3.11 - Use the definitions of the hyperbolic functions to...Ch. 3.11 - Prove the formulas given in Table 1 for the...Ch. 3.11 - Give an alternative solution 10 Example 3 by...Ch. 3.11 - Prob. 26ECh. 3.11 - Prove Equation 5 using (a) the method of Example 3...Ch. 3.11 - Prob. 28ECh. 3.11 - Prob. 29ECh. 3.11 - Find the derivative. Simplify where possible. 30....Ch. 3.11 - Find the derivative. Simplify where possible. 31....Ch. 3.11 - Find the derivative. Simplify where possible. 32....Ch. 3.11 - Find the derivative. Simplify where possible. 33....Ch. 3.11 - Prob. 34ECh. 3.11 - Find the derivative. Simplify where possible. 35....Ch. 3.11 - Find the derivative. Simplify where possible. 36....Ch. 3.11 - Find the derivative. Simplify where possible. 37....Ch. 3.11 - Prob. 38ECh. 3.11 - Find the derivative. Simplify where possible. 39....Ch. 3.11 - Prob. 40ECh. 3.11 - Find the derivative. Simplify where possible. 41....Ch. 3.11 - Find the derivative. Simplify where possible. 42....Ch. 3.11 - Find the derivative. Simplify where possible. 43....Ch. 3.11 - Prob. 44ECh. 3.11 - Prob. 45ECh. 3.11 - Prob. 46ECh. 3.11 - Prob. 47ECh. 3.11 - The Gateway Arch in St. Louis was designed by Eero...Ch. 3.11 - Prob. 49ECh. 3.11 - Prob. 50ECh. 3.11 - Prob. 51ECh. 3.11 - Prob. 52ECh. 3.11 - Prob. 53ECh. 3.11 - A model for the velocity of a falling object after...Ch. 3.11 - (a) Show that any function of the form y = A sinh...Ch. 3.11 - If x = ln( sec + tan ), show that sec = cosh x.Ch. 3.11 - At what point of the curve y = cosh x does the...Ch. 3.11 - Investigate the family of functions fn(x) = tanh...Ch. 3 - State each differentiation rule both in symbols...Ch. 3 - State the derivative of each function. (a) y = xn...Ch. 3 - (a) How is the number e defined? (b) Express e as...Ch. 3 - (a) Explain how implicit differentiation works....Ch. 3 - Give several examples of how the derivative can be...Ch. 3 - Prob. 6RCCCh. 3 - (a) Write an expression for the linearization of f...Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 10RQCh. 3 - Prob. 11RQCh. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 15RQCh. 3 - Calculate y'. 1. y = (x2 + x3)4Ch. 3 - Calculate y'. 2. y=1x1x35Ch. 3 - Prob. 3RECh. 3 - Calculate y'. 4. y=tanx1+cosxCh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Calculate y'. 8. xey = y sin xCh. 3 - Calculate y'. 9. y = ln(x ln x)Ch. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Calculate y'. 12. y = (arcsin 2x)2Ch. 3 - Prob. 13RECh. 3 - Calculate y'. 14. y = ln sec xCh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Calculate y'. 17. y=arctanCh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Calculate y'. 21. y = 3x ln xCh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Calculate y'. 24. y=1/x+x3Ch. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Calculate y'. 29. y=lnsinx12sin2xCh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Calculate y'. 33. y = ln | sec 5x + tan 5x |Ch. 3 - Prob. 34RECh. 3 - Calculate y'. 35. y = cot(3x2 + 5)Ch. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Calculate y'. 45. y = ln( cosh 3x)Ch. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Find y if x6 + y6 = 1.Ch. 3 - Find f(n)(x) if f(x) = 1/(2 x).Ch. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Find an equation of the tangent to the curve at...Ch. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Find equations of the tangent line and normal line...Ch. 3 - Find equations of the tangent line and normal line...Ch. 3 - If f(x) = xesin x find f(x). Graph f and f on the...Ch. 3 - Prob. 63RECh. 3 - (a) If f(x) = 4x tan x, /2 x /2, find f and f....Ch. 3 - At what points on the curve y = sin x + cos x, 0 ...Ch. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Suppose that f(1) = 2 f(1) = 3 f(2) = 1 f'(2) = 2...Ch. 3 - If f and g are the functions whose graphs are...Ch. 3 - Find f in terms of g. f(x) = x2g(x)Ch. 3 - Prob. 72RECh. 3 - Find f in terms of g. f(x) = [g(x)]2Ch. 3 - Prob. 74RECh. 3 - Find f in terms of g. f(x) = g(ex)Ch. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Find f in terms of g. f(x) = g(ln x)Ch. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Find f in terms of f and g. h(x) = f(g(sin 4x))Ch. 3 - Prob. 82RECh. 3 - At what point on the curve y = [ln(x + 4)]2 is the...Ch. 3 - (a) Find an equation of the tangent to the curve y...Ch. 3 - Prob. 85RECh. 3 - The function C(t) = K(eat ebt), where a, b, and K...Ch. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - A particle moves on a vertical line so that its...Ch. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - A bacteria culture contains 200 cells initially...Ch. 3 - Cobalt-60 has a half-life of 5.24 years. (a) Find...Ch. 3 - Let C(t) be the concentration of a drug in the...Ch. 3 - A cup of hot chocolate has temperature 80C in a...Ch. 3 - Prob. 97RECh. 3 - A paper cup has the shape of a cone with height 10...Ch. 3 - A balloon is rising at a constant speed of 5 ft/s....Ch. 3 - Prob. 100RECh. 3 - Prob. 101RECh. 3 - (a) Find the linear approximation to f(x)=25x2...Ch. 3 - (a) Find the linearization of f(x)1+3x3 at a = 0....Ch. 3 - Prob. 104RECh. 3 - A window has the shape of a square surmounted by a...Ch. 3 - Prob. 106RECh. 3 - Prob. 107RECh. 3 - Express the limit as a derivative and evaluate....Ch. 3 - Prob. 109RECh. 3 - Suppose f is a differentiable function such that...Ch. 3 - Prob. 111RECh. 3 - Show that the length of the portion of any tangent...Ch. 3 - Find points P and Q on the parabola y = 1 x2 so...Ch. 3 - Prob. 2PCh. 3 - Prob. 3PCh. 3 - Prob. 4PCh. 3 - If f(x)=limtxsectsecxtx, find the value of f'(/4).Ch. 3 - Find the values of the constants a and b such that...Ch. 3 - Show that sin-1(tanh x) = tan1(sinh x).Ch. 3 - Prob. 8PCh. 3 - Prove that dndxn(sin4x+cos4x)=4n1cos(4x+n/2).Ch. 3 - Prob. 10PCh. 3 - Prob. 11PCh. 3 - Find all values of r such that the parabolas y =...Ch. 3 - How many lines are tangent to both of the circles...Ch. 3 - Prob. 14PCh. 3 - The figure shows a rotating wheel with radius 40...Ch. 3 - Tangent lines T1, and T2, are drawn at two points...Ch. 3 - Prob. 17PCh. 3 - Prob. 18PCh. 3 - Prob. 19PCh. 3 - Prob. 20PCh. 3 - (a) Use the identity for tan(x y) (see Equation...Ch. 3 - Prob. 22PCh. 3 - Prob. 23PCh. 3 - Prob. 24PCh. 3 - Prob. 25PCh. 3 - For what value of k does the equation e2x=kx have...Ch. 3 - Prob. 28PCh. 3 - If y=xa212a21arctansinxa+a21+cosx show that...Ch. 3 - Given an ellipse x2/a2 + y2/b2 = 1, where a b,...Ch. 3 - Find the two points on the curve y = x4 2x2 x...Ch. 3 - Suppose that three points on the parabola y = x2...Ch. 3 - Prob. 33PCh. 3 - Prob. 34PCh. 3 - Prob. 35P
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
College Algebra
Algebra
ISBN:9781938168383
Author:Jay Abramson
Publisher:OpenStax
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Text book image
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Evaluating Indefinite Integrals; Author: Professor Dave Explains;https://www.youtube.com/watch?v=-xHA2RjVkwY;License: Standard YouTube License, CC-BY
Calculus - Lesson 16 | Indefinite and Definite Integrals | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=bMnMzNKL9Ks;License: Standard YouTube License, CC-BY