
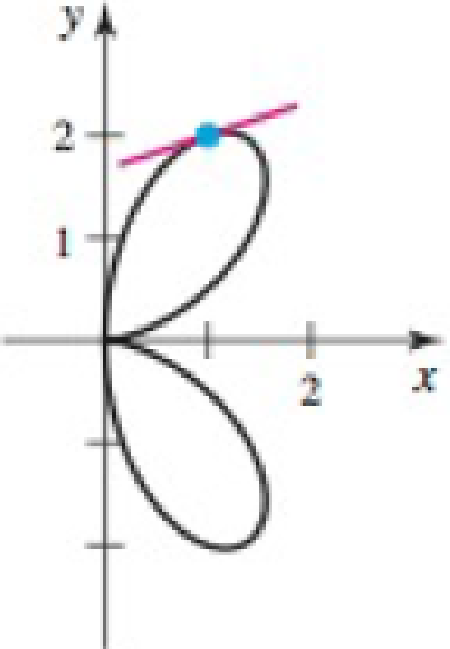
Tangent lines Carry out the following steps.
- a. Verify that the given point lies on the curve.
- b. Determine an equation of the line tangent to the curve at the given point.
30.
Trending nowThis is a popular solution!

Chapter 3 Solutions
Calculus: Early Transcendentals and MyLab Math with Pearson eText -- Title-Specific Access Card Package (3rd Edition) (Briggs, Cochran, Gillett & Schulz, Calculus Series)
Additional Math Textbook Solutions
Algebra and Trigonometry (6th Edition)
A First Course in Probability (10th Edition)
Elementary Statistics (13th Edition)
Thinking Mathematically (6th Edition)
College Algebra with Modeling & Visualization (5th Edition)
Elementary Statistics: Picturing the World (7th Edition)
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forward4. Use method of separation of variable to solve the following wave equation მłu J²u subject to u(0,t) =0, for t> 0, u(л,t) = 0, for t> 0, = t> 0, at² ax²' u(x, 0) = 0, 0.01 x, ut(x, 0) = Π 0.01 (π-x), 0arrow_forwardSolve the following heat equation by method of separation variables: ди = at subject to u(0,t) =0, for -16024 ძx2 • t>0, 0 0, ux (4,t) = 0, for t> 0, u(x, 0) = (x-3, \-1, 0 < x ≤2 2≤ x ≤ 4.arrow_forwardex 5. important aspects. Graph f(x)=lnx. Be sure to make your graph big enough to easily read (use the space given.) Label all 6 33arrow_forwardDecide whether each limit exists. If a limit exists, estimate its value. 11. (a) lim f(x) x-3 f(x) ↑ 4 3- 2+ (b) lim f(x) x―0 -2 0 X 1234arrow_forwardDetermine whether the lines L₁ (t) = (-2,3, −1)t + (0,2,-3) and L2 p(s) = (2, −3, 1)s + (-10, 17, -8) intersect. If they do, find the point of intersection.arrow_forwardConvert the line given by the parametric equations y(t) Enter the symmetric equations in alphabetic order. (x(t) = -4+6t = 3-t (z(t) = 5-7t to symmetric equations.arrow_forwardFind the point at which the line (t) = (4, -5,-4)+t(-2, -1,5) intersects the xy plane.arrow_forwardFind the distance from the point (-9, -3, 0) to the line ä(t) = (−4, 1, −1)t + (0, 1, −3) .arrow_forward1 Find a vector parallel to the line defined by the parametric equations (x(t) = -2t y(t) == 1- 9t z(t) = -1-t Additionally, find a point on the line.arrow_forwardFind the (perpendicular) distance from the line given by the parametric equations (x(t) = 5+9t y(t) = 7t = 2-9t z(t) to the point (-1, 1, −3).arrow_forwardLet ä(t) = (3,-2,-5)t + (7,−1, 2) and (u) = (5,0, 3)u + (−3,−9,3). Find the acute angle (in degrees) between the lines:arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning





