
Concept explainers
Interpretation:
To show there is always unstable fixed point at
Concept Introduction:
To check the stability at any point, differentiate the equation and put the value in it.
For small value of x predation is very weak, thus the budworm population increases exponentially, when
Answer to Problem 1E
Solution:
Instability at
Explanation of Solution
Given information:
The given expression is dimensionless for budworm population growth
Where
To check the stability of the equation at
By substituting
Given condition is
This result is also verified by plotting graph for equation
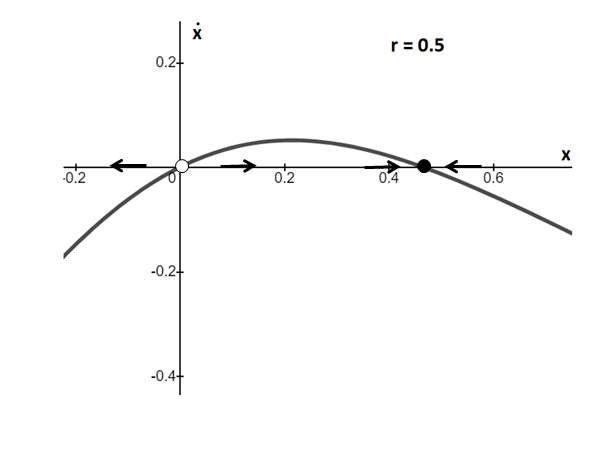
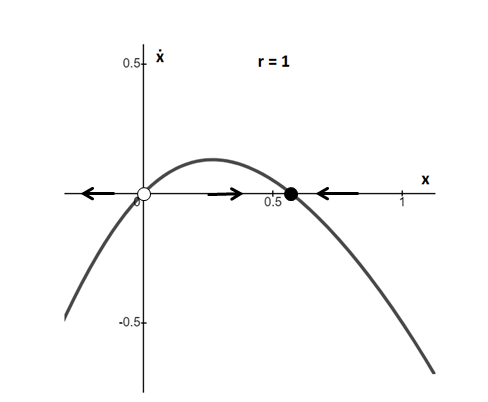
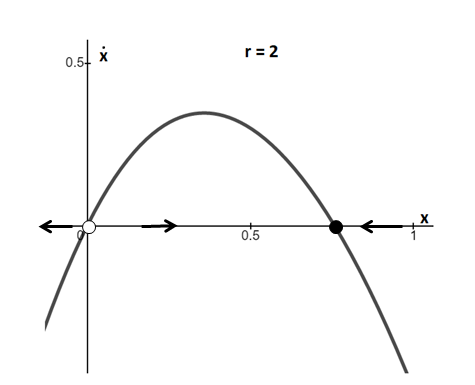
From the above graphs, it is clear that for
For the given type of system, there is always an unstable fixed point at
Want to see more full solutions like this?
Chapter 3 Solutions
EBK NONLINEAR DYNAMICS AND CHAOS WITH S
- Find the closed formula for each of the following sequences (a_n)_n>=1 by realting them to a well known sequence. Assume the first term given is a_1 d. 5,23,119,719,5039 i have tried finding the differnces and the second difference and i still dont see the patternarrow_forwardYou manage a chemical company with 2 warehouses. The following quantities of Important Chemical A have arrived from an international supplier at 3 different ports: Chemical Available (L) Port 1 Port 2 Port 3 400 110 100 The following amounts of Important Chemical A are required at your warehouses: Warehouse 1 Warehouse 2 Chemical Required (L) 380 230 The cost in £ to ship 1L of chemical from each port to each warehouse is as follows: Warehouse 1 Warehouse 2 Port 1 £10 £45 Port 2 £20 £28 Port 3 £13 £11 (a) You want to know how to send these shipments as cheaply as possible. For- mulate this as a linear program (you do not need to formulate it in standard inequality form) indicating what each variable represents.arrow_forwarda) Suppose that we are carrying out the 1-phase simplex algorithm on a linear program in standard inequality form (with 3 variables and 4 constraints) and suppose that we have reached a point where we have obtained the following tableau. Apply one more pivot operation, indicating the highlighted row and column and the row operations you carry out. What can you conclude from your updated tableau? x1 12 23 81 82 83 S4 $1 -20 1 1 0 0 0 3 82 3 0 -2 0 1 2 0 6 12 1 1 -3 0 0 1 0 2 84 -3 0 2 0 0 -1 1 4 2 -2 0 11 0 0 -4 0 -8 b) Solve the following linear program using the 2-phase simplex algorithm. You should give the initial tableau and each further tableau produced during the execution of the algorithm. If the program has an optimal solution, give this solution and state its objective value. If it does not have an optimal solution, say why. maximize 21 - - 2x2 + x3 - 4x4 subject to 2x1+x22x3x4≥ 1, 5x1+x2-x3-4 -1, 2x1+x2-x3-342, 1, 2, 3, 4 ≥0.arrow_forward
- Suppose we have a linear program in standard equation form maximize c'x subject to Ax=b, x≥ 0. and suppose u, v, and w are all optimal solutions to this linear program. (a) Prove that zu+v+w is an optimal solution. (b) If you try to adapt your proof from part (a) to prove that that u+v+w is an optimal solution, say exactly which part(s) of the proof go wrong. (c) If you try to adapt your proof from part (a) to prove that u+v-w is an optimal solution, say exactly which part(s) of the proof go wrong.arrow_forward(a) For the following linear programme, sketch the feasible region and the direction of the objective function. Use you sketch to find an optimal solution to the program. State the optimal solution and give the objective value for this solution. maximize +22 subject to 1 + 2x2 ≤ 4, 1 +3x2 ≤ 12, x1, x2 ≥0 (b) For the following linear programme, sketch the feasible region and the direction of the objective function. Explain, making reference to your sketch, why this linear programme is unbounded. maximize ₁+%2 subject to -2x1 + x2 ≤ 4, x1 - 2x2 ≤4, x1 + x2 ≥ 7, x1,x20 Give any feasible solution to the linear programme for which the objective value is 40 (you do not need to justify your answer).arrow_forwardfind the domain of the function f(x)arrow_forward
- For each of the following functions, find the Taylor Series about the indicated center and also determine the interval of convergence for the series. 1. f(x) = ex-2, c = 2 Π == 2. f(x) = sin(x), c = 2arrow_forwardQUESTION 5. Show that if 0 ≤r≤n, then r+2 r r (c) + (+³) + (+³) +- + (*) -(+) n n+ = r (1)...using induction on n. (2) ...using a combinatorial proof.arrow_forwardUse a power series to approximate each of the following to within 3 decimal places: 1. arctan 2. In (1.01)arrow_forward
- For each of the following power series, find the interval of convergence and the radius of convergence: n² 1.0 (x + 1)" n=1 շո 3n 2. Σ n=1 (x-3)n n3arrow_forwardUse a known series to find a power series in x that has the given function as its sum: 1. xcos(x³) 2. In (1+x) xarrow_forwardif n is odd integer then 4 does not divide narrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning


