PRECALCULAS-ALEKS 360 ACCESS CODE
17th Edition
ISBN: 9781264003594
Author: Miller
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3.6, Problem 32PE
The population of Canada
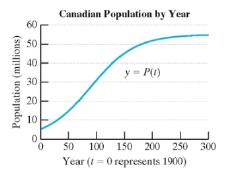
a. Evaluate
b. Use the function to approximate the Canadian population on January 1, 2015. Round to the nearest tenth of a million?
c. Use the function to approximate the Canadian population on January 1, 2040.
d. From the model, during which year would the Canadian population reach 45 million?
e. What value will the term
f. Determine the limiting value of
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Use undetermined coefficients to find the particular solution to
y"-y+5y = 7t² +61 +3
Yp(t) =
Please refer below
Question attached
Chapter 3 Solutions
PRECALCULAS-ALEKS 360 ACCESS CODE
Ch. 3.1 - Determine whether the function is one-to-one....Ch. 3.1 - Use the horizontal line test to determine if the...Ch. 3.1 - Determine whether the function is one-to-one....Ch. 3.1 - Determine whether the functions are inverses....Ch. 3.1 - Write an equation for the inverse function for...Ch. 3.1 - Write an equation for the inverse function for the...Ch. 3.1 - Given nx=x2+1forx0, write an equation of the...Ch. 3.1 - Given gx=x+2, find an equation of the inverse.Ch. 3.1 - Given the function f=1,2,2,3,3,4 write the set of...Ch. 3.1 - The graphs of a function and its inverse are...
Ch. 3.1 - If no horizontal line intersects the graph of a...Ch. 3.1 - Given a one-to one function f, if fa=fb,thenab.Ch. 3.1 - Let f be a one-to-one function and let g be the...Ch. 3.1 - If a,b is a point on the graph of a one-to-one...Ch. 3.1 - For Exercises 7-12, a relation in x and y is...Ch. 3.1 - For Exercises 7-12, a relation in x and y is...Ch. 3.1 - For Exercises 7-12, a relation in x and y is...Ch. 3.1 - For Exercises 7-12, a relation in x and y is...Ch. 3.1 - For Exercises 7-12, a relation in x and y is...Ch. 3.1 - For Exercises 7-12, a relation in x and y is...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 13-22, determine if the relation...Ch. 3.1 - For Exercises 23-30, use the definition of a...Ch. 3.1 - For Exercises 23-30, use the definition of a...Ch. 3.1 - For Exercises 23-30, use the definition of a...Ch. 3.1 - For Exercises 23-30, use the definition of a...Ch. 3.1 - For Exercises 23-30, use the definition of a...Ch. 3.1 - For Exercises 23-30, use the definition of a...Ch. 3.1 - For Exercises 23-30, use the definition of a...Ch. 3.1 - For Exercises 23-30, use the definition of a...Ch. 3.1 - For Exercises 31-36, determine whether the two...Ch. 3.1 - For Exercises 31-36, determine whether the two...Ch. 3.1 - For Exercises 31-36, determine whether the two...Ch. 3.1 - For Exercises 31-36, determine whether the two...Ch. 3.1 - For Exercises 31-36, determine whether the two...Ch. 3.1 - For Exercises 31-36, determine whether the two...Ch. 3.1 - There were 2000 applicants for enrollment to the...Ch. 3.1 - The monthly sales for January for a whole foods...Ch. 3.1 - a. Show that fx=2x3 defines a one-to-one function....Ch. 3.1 - a. Show that fx=4x+4 defines a one-to-one...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - For Exercises 41-52, a one-to-one function is...Ch. 3.1 - a. Graph fx=x23;x0. (See Example 7) b. From the...Ch. 3.1 - a. Graph fx=x2+1;x0. b. From the graph of f , is f...Ch. 3.1 - a. Graph fx=x+1. (See Example 8) b. From the graph...Ch. 3.1 - a. Graph fx=x2. b. From the graph of f , is f a...Ch. 3.1 - Given that the domain of a one-to-one function f...Ch. 3.1 - Given that the domain of a one-to-one function f...Ch. 3.1 - Given fx=x+3;x0, write an equation for f1 .Ch. 3.1 - Given fx=x3;x0, write an equation for f1 .Ch. 3.1 - For Exercises 61-66, fill in the blanks and...Ch. 3.1 - For Exercises 61-66, fill in the blanks and...Ch. 3.1 - For Exercises 61-66, fill in the blanks and...Ch. 3.1 - For Exercises 61-66, fill in the blanks and...Ch. 3.1 - For Exercises 61-66, fill in the blanks and...Ch. 3.1 - For Exercises 61-66, fill in the blanks and...Ch. 3.1 - For Exercises 67-70, find the inverse mentally....Ch. 3.1 - For Exercises 67-70, find the inverse mentally....Ch. 3.1 - For Exercises 67-70, find the inverse mentally....Ch. 3.1 - For Exercises 67-70, find the inverse mentally....Ch. 3.1 - For Exercises 71-74, the graph of a function is...Ch. 3.1 - For Exercises 71-74, the graph of a function is...Ch. 3.1 - For Exercises 71-74, the graph of a function is...Ch. 3.1 - Prob. 74PECh. 3.1 - For Exercises 75-76, the table defines Y1=fx as a...Ch. 3.1 - For Exercises 75-76, the table defines Y1=fx as a...Ch. 3.1 - For Exercises 77-80, determine if the statement is...Ch. 3.1 - For Exercises 77-80, determine if the statement is...Ch. 3.1 - For Exercises 77-80, determine if the statement is...Ch. 3.1 - For Exercises 77-80, determine if the statement is...Ch. 3.1 - Based on data from Hurricane Katrina, the function...Ch. 3.1 - The function defined by Fx=95x+32 gives the...Ch. 3.1 - Suppose that during normal respiration, the volume...Ch. 3.1 - At a cruising altitude of 35,000 ft, a certain...Ch. 3.1 - The millage rate is the amount of property tax per...Ch. 3.1 - Beginning on January 1, park rangers in Everglades...Ch. 3.1 - Prob. 87PECh. 3.1 - Prob. 88PECh. 3.1 - Explain why if a horizontal line intersects the...Ch. 3.1 - Prob. 90PECh. 3.1 - Prob. 91PECh. 3.1 - Consider a function defined as follows: Given x,...Ch. 3.1 - Prob. 93PECh. 3.1 - A function is said to be periodic if there exists...Ch. 3.2 - Graph the functions. a.fx=5xb.gx=15xCh. 3.2 - Graph. gx=2x+21Ch. 3.2 - Explain how the graph of fx=ex1 is related to the...Ch. 3.2 - Suppose that $8000 is invested and pays 4.5% per...Ch. 3.2 - Cesium-137 is a radioactive metal with a short...Ch. 3.2 - The function defined by y=x3 (is/is not) an...Ch. 3.2 - The graph of fx=53x is (increasing/decreasing)...Ch. 3.2 - The graph of fx=35x is (increasing/decreasing)...Ch. 3.2 - The domain of an exponential function fx=bxis.Ch. 3.2 - The range of an exponential function fx=bxis.Ch. 3.2 - All exponential functions fx=bx pass through the...Ch. 3.2 - The horizontal asymptote of an exponential...Ch. 3.2 - As x, the value of 1+1xx approaches .Ch. 3.2 - For Exercises 9-12, evaluate the functions the...Ch. 3.2 - For Exercises 9-12, evaluate the functions the...Ch. 3.2 - For Exercises 9-12, evaluate the functions the...Ch. 3.2 - For Exercises 9-12, evaluate the functions the...Ch. 3.2 - Which function are exponential functions?...Ch. 3.2 - Which function are exponential functions?...Ch. 3.2 - For Exercises 15-22, graph the functions and write...Ch. 3.2 - For Exercises 15-22, graph the functions and write...Ch. 3.2 - For Exercises 15-22, graph the functions and write...Ch. 3.2 - For Exercises 15-22, graph the functions and write...Ch. 3.2 - For Exercises 15-22, graph the functions and write...Ch. 3.2 - For Exercises 15-22, graph the functions and write...Ch. 3.2 - For Exercises 15-22, graph the functions and write...Ch. 3.2 - For Exercises 15-22, graph the functions and write...Ch. 3.2 - For Exercises 23-32, a. Use transformations of the...Ch. 3.2 - For Exercises 23-32, a. Use transformations of the...Ch. 3.2 - For Exercises 23-32, a. Use transformations of the...Ch. 3.2 - Prob. 26PECh. 3.2 - For Exercises 23-32, a. Use transformations of the...Ch. 3.2 - For Exercises 23-32, a. Use transformations of the...Ch. 3.2 - For Exercises 23-32, a. Use transformations of the...Ch. 3.2 - For Exercises 23-32, a. Use transformations of the...Ch. 3.2 - For Exercises 23-32, a. Use transformations of the...Ch. 3.2 - For Exercises 23-32, a. Use transformations of the...Ch. 3.2 - For Exercises 33-36, a. Use transformations of the...Ch. 3.2 - For Exercises 33-36, a. Use transformations of the...Ch. 3.2 - Prob. 35PECh. 3.2 - Prob. 36PECh. 3.2 - For Exercises 37-38, evaluate the functions for...Ch. 3.2 - Prob. 38PECh. 3.2 - Prob. 39PECh. 3.2 - For Exercises 39-44, a. Use transformations of the...Ch. 3.2 - For Exercises 39-44, a. Use transformations of the...Ch. 3.2 - Prob. 42PECh. 3.2 - For Exercises 39-44, a. Use transformations of the...Ch. 3.2 - For Exercises 39-44, a. Use transformations of the...Ch. 3.2 - For Exercises 45-46, complete the table to...Ch. 3.2 - For Exercises 45-46, complete the table to...Ch. 3.2 - Prob. 47PECh. 3.2 - For Exercises 47-48, suppose that P dollars in...Ch. 3.2 - Prob. 49PECh. 3.2 - Al needs to borrow $15,000 to buy a car. He can...Ch. 3.2 - Jerome wants to invest $25,000 as part of his...Ch. 3.2 - Heather wants to invest $35,000 of her retirement....Ch. 3.2 - Strontium-90 90Sr is a by-product of nuclear...Ch. 3.2 - In 2006, the murder of Alexander Litvinenko a...Ch. 3.2 - According to the CIA’s World Fact Book in 2010,...Ch. 3.2 - The population of Canada in 2010 was approximately...Ch. 3.2 - The atmospheric pressure on an object decreases as...Ch. 3.2 - The function defined by At=100e0.0318t...Ch. 3.2 - Newton's law of cooling Indicates that the...Ch. 3.2 - Newton's law of cooling Indicates that the...Ch. 3.2 - A farmer depreciates a $120,000 tractor. He...Ch. 3.2 - A veterinarian depreciates a $10,000 X-ray...Ch. 3.2 - For Exercises 63-64, solve the equation in parts...Ch. 3.2 - For Exercises 63-64, solve the equation in parts...Ch. 3.2 - a. Graph fx=2x. (See Example 1) b. Is f a...Ch. 3.2 - Prob. 66PECh. 3.2 - Refer to the graphs of fx=2x and the inverse...Ch. 3.2 - Refer to the graphs of gx=3x and the inverse...Ch. 3.2 - Explain why the equation 2x=2 has no solution.Ch. 3.2 - Explain why the fx=x2 is not an exponential...Ch. 3.2 - For Exercises 71-72, find the real solutions to...Ch. 3.2 - For Exercises 71-72, find the real solutions to...Ch. 3.2 - Use the properties of exponents to simplify....Ch. 3.2 - Factor. a.ex+hexb.e4xe2xCh. 3.2 - Multiply. ex+ex2Ch. 3.2 - Multiply. exex2Ch. 3.2 - Show that ex+ex22exex22=1.Ch. 3.2 - Prob. 78PECh. 3.2 - Prob. 79PECh. 3.2 - For Exercises 79-80, find the difference quotient...Ch. 3.2 - Graph the following functions on the window...Ch. 3.3 - Write each equation in exponential form....Ch. 3.3 - Write each equation in logarithmic form....Ch. 3.3 - Evaluate each expression....Ch. 3.3 - Evaluate. a.log10,000,000b.log0.1c.lne5d.lneCh. 3.3 - Approximate the logarithms. Round to 4 decimal...Ch. 3.3 - Simplify....Ch. 3.3 - Graph the functions. a.y=log4xb.y=log1/2xCh. 3.3 - Graph the function. Identify the vertical...Ch. 3.3 - Write the domain in interval notation....Ch. 3.3 - a. Determine the magnitude of an earthquake that...Ch. 3.3 - Given positive real numbers x and b such that...Ch. 3.3 - Given y=logbx, the value y is called the , b is...Ch. 3.3 - The logarithmic function base 10 is called the ...Ch. 3.3 - Given y=logx, the base is understood to be . Given...Ch. 3.3 - logb1= because b=1.Ch. 3.3 - logbb= because b=b.Ch. 3.3 - f(x)=logbxandg(x)=bx are inverse functions...Ch. 3.3 - The graph of y=logbx passes through the point (1,...Ch. 3.3 - For Exercises 9-16, write the equation in...Ch. 3.3 - For Exercises 9-16, write the equation in...Ch. 3.3 - For Exercises 9-16, write the equation in...Ch. 3.3 - For Exercises 9-16, write the equation in...Ch. 3.3 - For Exercises 9-16, write the equation in...Ch. 3.3 - For Exercises 9-16, write the equation in...Ch. 3.3 - Prob. 15PECh. 3.3 - Prob. 16PECh. 3.3 - Prob. 17PECh. 3.3 - For Exercises 17-24, write the equation in...Ch. 3.3 - Prob. 19PECh. 3.3 - For Exercises 17-24, write the equation in...Ch. 3.3 - Prob. 21PECh. 3.3 - For Exercises 17-24, write the equation in...Ch. 3.3 - Prob. 23PECh. 3.3 - For Exercises 17-24, write the equation in...Ch. 3.3 - Prob. 25PECh. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - Prob. 27PECh. 3.3 - Prob. 28PECh. 3.3 - Prob. 29PECh. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - Prob. 31PECh. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - Prob. 33PECh. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - Prob. 35PECh. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - Prob. 37PECh. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - Prob. 39PECh. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - Prob. 41PECh. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - Prob. 45PECh. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - For Exercises 25-50, simplify the expression...Ch. 3.3 - Prob. 48PECh. 3.3 - Prob. 49PECh. 3.3 - Prob. 50PECh. 3.3 - For Exercises 51-52, estimate the value of each...Ch. 3.3 - For Exercises 51-52, estimate the value of each...Ch. 3.3 - Prob. 53PECh. 3.3 - For Exercises 53-54, approximate fx=lnx for the...Ch. 3.3 - For Exercises 55-64, simplify the expression...Ch. 3.3 - For Exercises 55-64, simplify the expression...Ch. 3.3 - For Exercises 55-64, simplify the expression...Ch. 3.3 - For Exercises 55-64, simplify the expression...Ch. 3.3 - Prob. 59PECh. 3.3 - For Exercises 55-64, simplify the expression...Ch. 3.3 - For Exercises 55-64, simplify the expression...Ch. 3.3 - For Exercises 55-64, simplify the expression...Ch. 3.3 - For Exercises 55-64, simplify the expression...Ch. 3.3 - For Exercises 55-64, simplify the expression...Ch. 3.3 - For Exercises 65-70, graph the function. (See...Ch. 3.3 - For Exercises 65-70, graph the function. (See...Ch. 3.3 - Prob. 67PECh. 3.3 - Prob. 68PECh. 3.3 - Prob. 69PECh. 3.3 - Prob. 70PECh. 3.3 - Prob. 71PECh. 3.3 - Prob. 72PECh. 3.3 - Prob. 73PECh. 3.3 - Prob. 74PECh. 3.3 - Prob. 75PECh. 3.3 - For Exercises 71-78, (See Example 8) a. Use...Ch. 3.3 - Prob. 77PECh. 3.3 - Prob. 78PECh. 3.3 - Prob. 79PECh. 3.3 - For Exercises 79-92, write the domain in interval...Ch. 3.3 - For Exercises 79-92, write the domain in interval...Ch. 3.3 - For Exercises 79-92, write the domain in interval...Ch. 3.3 - Prob. 83PECh. 3.3 - Prob. 84PECh. 3.3 - Prob. 85PECh. 3.3 - Prob. 86PECh. 3.3 - For Exercises 79-92, write the domain in interval...Ch. 3.3 - For Exercises 79-92, write the domain in interval...Ch. 3.3 - Prob. 89PECh. 3.3 - For Exercises 79-92, write the domain in interval...Ch. 3.3 - Prob. 91PECh. 3.3 - Prob. 92PECh. 3.3 - Prob. 93PECh. 3.3 - The intensities of earthquakes are measured with...Ch. 3.3 - Sounds are produced when vibrating objects create...Ch. 3.3 - Sounds are produced when vibrating objects create...Ch. 3.3 - Scientists use the pH scale to represent the level...Ch. 3.3 - Scientists use the pH scale to represent the level...Ch. 3.3 - Prob. 99PECh. 3.3 - For Exercises 99-102, a. Write the equation in...Ch. 3.3 - For Exercises 99-102, a. Write the equation in...Ch. 3.3 - For Exercises 99-102, a. Write the equation in...Ch. 3.3 - For Exercises 103-106, evaluate the expressions....Ch. 3.3 - For Exercises 103-106, evaluate the expressions....Ch. 3.3 - For Exercises 103-106, evaluate the expressions....Ch. 3.3 - For Exercises 103-106, evaluate the expressions....Ch. 3.3 - a. Evaluate log22+log24 b. Evaluate log224 c. How...Ch. 3.3 - a. Evaluate log33+log327 b. Evaluate log3327 c....Ch. 3.3 - a. Evaluate log464log44 b. Evaluate log4644 c. How...Ch. 3.3 - a. Evaluate log100,000log100 b. Evaluate...Ch. 3.3 - a. Evaluate log225 b. Evaluate 5log22 c. How do...Ch. 3.3 - a. Evaluate log776 b. Evaluate 6log77 c. How do...Ch. 3.3 - a. The time t (in years) required for an...Ch. 3.3 - a. The number n of monthly payments of P dollars...Ch. 3.3 - For Exercises 115-116, use a calculator to...Ch. 3.3 - For Exercises 115-116, use a calculator to...Ch. 3.3 - Prob. 117PECh. 3.3 - Prob. 118PECh. 3.3 - Prob. 119PECh. 3.3 - Prob. 120PECh. 3.3 - Prob. 121PECh. 3.3 - Prob. 122PECh. 3.3 - Prob. 123PECh. 3.3 - Prob. 124PECh. 3.3 - Prob. 125PECh. 3.3 - Prob. 126PECh. 3.3 - Prob. 1PRECh. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.3 - For Exercises 1-14, a. Write the domain. b. Write...Ch. 3.4 - Write the logarithm as a sum and simplify if...Ch. 3.4 - Write the logarithm as the difference of...Ch. 3.4 - Apply the power property of logarithms....Ch. 3.4 - Write the expression as the sum or difference of...Ch. 3.4 - Write the expression as a single logarithm and...Ch. 3.4 - Write the expression as a single logarithm and...Ch. 3.4 - Given that logb20.356andlogb30.565, approximate...Ch. 3.4 - a. Estimate log623 between two consecutive...Ch. 3.4 - The product property of logarithms states that...Ch. 3.4 - The property of logarithms states that logbxy=...Ch. 3.4 - The power property of logarithms states that for...Ch. 3.4 - The change-of-base formula states that logbx can...Ch. 3.4 - The change-of-base formula is often used to...Ch. 3.4 - To use a graphing utility to graph the function...Ch. 3.4 - Prob. 7PECh. 3.4 - For Exercises 7-12, use the product property of...Ch. 3.4 - For Exercises 7-12, use the product property of...Ch. 3.4 - For Exercises 7-12, use the product property of...Ch. 3.4 - For Exercises 7-12, use the product property of...Ch. 3.4 - For Exercises 7-12, use the product property of...Ch. 3.4 - For Exercises 13-18, use the quotient property of...Ch. 3.4 - For Exercises 13-18, use the quotient property of...Ch. 3.4 - For Exercises 13-18, use the quotient property of...Ch. 3.4 - For Exercises 13-18, use the quotient property of...Ch. 3.4 - For Exercises 13-18, use the quotient property of...Ch. 3.4 - For Exercises 13-18, use the quotient property of...Ch. 3.4 - Prob. 19PECh. 3.4 - For Exercises 19-24, apply the power property of...Ch. 3.4 - Prob. 21PECh. 3.4 - For Exercises 19-24, apply the power property of...Ch. 3.4 - Prob. 23PECh. 3.4 - For Exercises 19-24, apply the power property of...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - Prob. 28PECh. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - Prob. 30PECh. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - Prob. 36PECh. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - For Exercises 25-44, write the logarithm as a sum...Ch. 3.4 - Prob. 44PECh. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - Prob. 46PECh. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - Prob. 66PECh. 3.4 - For Exercises 45-68, write the logarithmic...Ch. 3.4 - Prob. 68PECh. 3.4 - Prob. 69PECh. 3.4 - Prob. 70PECh. 3.4 - Prob. 71PECh. 3.4 - For Exercises 69-78, use...Ch. 3.4 - Prob. 73PECh. 3.4 - For Exercises 69-78, use...Ch. 3.4 - For Exercises 69-78, use...Ch. 3.4 - Prob. 76PECh. 3.4 - For Exercises 69-78, use...Ch. 3.4 - For Exercises 69-78, use...Ch. 3.4 - For Exercises 79-84, (See Example 8) a. Estimate...Ch. 3.4 - For Exercises 79-84, (See Example 8) a. Estimate...Ch. 3.4 - For Exercises 79-84, (See Example 8) a. Estimate...Ch. 3.4 - For Exercises 79-84, (See Example 8) a. Estimate...Ch. 3.4 - For Exercises 79-84, (See Example 8) a. Estimate...Ch. 3.4 - For Exercises 79-84, (See Example 8) a. Estimate...Ch. 3.4 - For Exercises 85-88, use the change-of-base...Ch. 3.4 - For Exercises 85-88, use the change-of-base...Ch. 3.4 - For Exercises 85-88, use the change-of-base...Ch. 3.4 - For Exercises 85-88, use the change-of-base...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - For Exercises 89-98, determine if the statement is...Ch. 3.4 - Explain why the product property of logarithms...Ch. 3.4 - Explain how to use the change-of-base formula and...Ch. 3.4 - a. Write the difference quotient for fx=lnx. b....Ch. 3.4 - Show that lnxx21=lnx+x21Ch. 3.4 - Show that logb+b24ac2a+logbb24ac2a=logclogaCh. 3.4 - Show that lnc+c2x2cc2x2=2lnc+c2x22lnxCh. 3.4 - Use the change-of-base formula to write log25log59...Ch. 3.4 - Use the change-of-base formula to write...Ch. 3.4 - Prove the quotient property of logarithms:...Ch. 3.4 - Prove the power property of logarithms:...Ch. 3.4 - For Exercises 109-112, graph the function....Ch. 3.4 - For Exercises 109-112, graph the function....Ch. 3.4 - For Exercises 109-112, graph the function....Ch. 3.4 - For Exercises 109-112, graph the function....Ch. 3.4 - a. Graph Y1=logxandY2=12logx2. How are the graphs...Ch. 3.4 - Graph Y1=ln0.1x,Y2=ln0.5x,Y3=lnx,andY4=ln2x. How...Ch. 3.5 - Solve. a.42x3=64b.272w+5=1325wCh. 3.5 - Solve. 5x=83Ch. 3.5 - Solve. a.400+104x1=63,000b.100=700e0.2kCh. 3.5 - Solve. 35x6=24x+1Ch. 3.5 - Solve. e2x5ex14=0Ch. 3.5 - Solve. log27x4=log22x+1Ch. 3.5 - Solve. lnx+lnx8=lnx20Ch. 3.5 - Solve. 8log4w+6=24Ch. 3.5 - Solve. logt18=1.4Ch. 3.5 - Solve. 2log7x=log7x48Ch. 3.5 - Determine how long it will take $8000 compounded...Ch. 3.5 - a. Find the intensity of sound form a leaf blower...Ch. 3.5 - An equation such as 4x=9 is called an equation...Ch. 3.5 - Prob. 2PECh. 3.5 - The equivalence property of logarithmic...Ch. 3.5 - An equation containing a variable within a...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 5-16, solve the equation. (See...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 17-34, solve the equation. Write the...Ch. 3.5 - For Exercises 35-36, determine if the given value...Ch. 3.5 - For Exercises 35-36, determine if the given value...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 37-60, solve the equation. Write the...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - For Exercises 61-70, use the model...Ch. 3.5 - Physicians often treat thyroid cancer with a...Ch. 3.5 - Caffeine occurs naturally in a variety of food...Ch. 3.5 - Sunlight is absorbed in water, and as a result the...Ch. 3.5 - Sunlight is absorbed in water, and as a result the...Ch. 3.5 - Sunlight is absorbed in water, and as a result the...Ch. 3.5 - Sunlight is absorbed in water, and as a result the...Ch. 3.5 - Forge welding is a process in which two pieces of...Ch. 3.5 - A pie comes out of the oven at 325oF and is placed...Ch. 3.5 - Prob. 79PECh. 3.5 - For Exercises 79-80, the formula L=10logII0 gives...Ch. 3.5 - Prob. 81PECh. 3.5 - Prob. 82PECh. 3.5 - A new teaching method to teach vocabulary to...Ch. 3.5 - Prob. 84PECh. 3.5 - Radiated seismic energy from an earthquake is...Ch. 3.5 - On August 31, 1854, an epidemic of cholera was...Ch. 3.5 - For Exercises 87-94, find an equation for the...Ch. 3.5 - For Exercises 87-94, find an equation for the...Ch. 3.5 - For Exercises 87-94, find an equation for the...Ch. 3.5 - For Exercises 87-94, find an equation for the...Ch. 3.5 - For Exercises 87-94, find an equation for the...Ch. 3.5 - For Exercises 87-94, find an equation for the...Ch. 3.5 - For Exercises 87-94, find an equation for the...Ch. 3.5 - For Exercises 87-94, find an equation for the...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - Prob. 104PECh. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - For Exercises 95-112, solve the equation. Write...Ch. 3.5 - Explain the process to solve the equation 4x=11.Ch. 3.5 - Prob. 114PECh. 3.5 - Prob. 115PECh. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - Prob. 118PECh. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - For Exercises 115-126, solve the equation....Ch. 3.5 - For Exercises 127-130, an equation is given in the...Ch. 3.5 - For Exercises 127-130, an equation is given in the...Ch. 3.5 - For Exercises 127-130, an equation is given in the...Ch. 3.5 - For Exercises 127-130, an equation is given in the...Ch. 3.6 - a. Given T=78+272ekt,solvefork. b. Given...Ch. 3.6 - Suppose that $10,000 is invested and at the end of...Ch. 3.6 - On January 1, 2000, the population of Texas was...Ch. 3.6 - a. Given Pt=10,00020.4t, write the rule for this...Ch. 3.6 - Use the function Qt=Q0e0.000121t to determine the...Ch. 3.6 - The score on a test of dexterity is by...Ch. 3.6 - For the given data, a. Graph the data points. b....Ch. 3.6 - For the given data, a. Graph the data points. b....Ch. 3.6 - If k0, the equation y=y0ekt is a model for...Ch. 3.6 - A function defined by y=abx can be written in...Ch. 3.6 - A function defined by y=c1+aebt is called a ...Ch. 3.6 - Given a logistic function y=c1+aebt , the limiting...Ch. 3.6 - For Exercises 5-14, solve for the indicated...Ch. 3.6 - For Exercises 5-14, solve for the indicated...Ch. 3.6 - For Exercises 5-14, solve for the indicated...Ch. 3.6 - For Exercises 5-14, solve for the indicated...Ch. 3.6 - For Exercises 5-14, solve for the indicated...Ch. 3.6 - For Exercises 5-14, solve for the indicated...Ch. 3.6 - For Exercises 5-14, solve for the indicated...Ch. 3.6 - For Exercises 5-14, solve for the indicated...Ch. 3.6 - For Exercises 5-14, solve for the indicated...Ch. 3.6 - Prob. 14PECh. 3.6 - Suppose that $12,000 is invested in a bond fund...Ch. 3.6 - Suppose that $50,000 from a retirement account is...Ch. 3.6 - Suppose that P dollars in principal is invested in...Ch. 3.6 - Suppose that P dollars in principal is invested in...Ch. 3.6 - The populations of two countries are given for...Ch. 3.6 - The populations of two countries are given for...Ch. 3.6 - A function of the form Pt=abt represents the...Ch. 3.6 - A function of the form Pt=abt represents the...Ch. 3.6 - Prob. 23PECh. 3.6 - For Exercises 23-24, refer to the model...Ch. 3.6 - The isotope of plutonium 238Pu is used to make...Ch. 3.6 - Technetium-99 99mTc is a radionuclide used widely...Ch. 3.6 - Fluorodeoxyglucose is a derivative of glucose that...Ch. 3.6 - Painful bone metastases are common in advanced...Ch. 3.6 - Two million E. coli bacteria are present in a...Ch. 3.6 - The half-life of radium-226 is 1620 yr. Given a...Ch. 3.6 - The population of the United States Pt (in...Ch. 3.6 - The population of Canada Pt (in millions) since...Ch. 3.6 - The number of computers Nt (in millions) infected...Ch. 3.6 - After a new product is launched the cumulative...Ch. 3.6 - For Exercises 35-38, a graph of data is given....Ch. 3.6 - For Exercises 35-38, a graph of data is given....Ch. 3.6 - For Exercises 35-38, a graph of data is given....Ch. 3.6 - For Exercises 35-38, a graph of data is given....Ch. 3.6 - For Exercises 39-46, a table of data is given. a....Ch. 3.6 - For Exercises 39-46, a table of data is given. a....Ch. 3.6 - For Exercises 39-46, a table of data is given. a....Ch. 3.6 - For Exercises 39-46, a table of data is given. a....Ch. 3.6 - For Exercises 39-46, a table of data is given. a....Ch. 3.6 - For Exercises 39-46, a table of data is given. a....Ch. 3.6 - For Exercises 39-46, a table of data is given. a....Ch. 3.6 - For Exercises 39-46, a table of data is given. a....Ch. 3.6 - During a recent outbreak of Ebola in western...Ch. 3.6 - The monthly costs for a small company to do...Ch. 3.6 - The age of a tree t (in yr) and its corresponding...Ch. 3.6 - The sales of a book tend to increase over the...Ch. 3.6 - A van is purchased new for $29,200. a. Write a...Ch. 3.6 - A delivery truck is purchased new for $54,000 . a....Ch. 3.6 - Why is it important to graph a set of data before...Ch. 3.6 - Prob. 54PECh. 3.6 - Prob. 55PECh. 3.6 - Explain how to convert an exponential expression...Ch. 3.6 - Prob. 57PECh. 3.6 - Suppose that a population follows a logistic...Ch. 3 - For Exercises 1-2, determine if the relation...Ch. 3 - For Exercises 1-2, determine if the relation...Ch. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - a. Graph fx=x29,x0. b. Is f a one-to-one function?...Ch. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - For Exercises 13-16, a. Graph the function. b....Ch. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - A patient is treated with 128 mCi (millicuries) of...Ch. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - For Exercises 25-32, simplify the logarithmic...Ch. 3 - For Exercises 25-32, simplify the logarithmic...Ch. 3 - For Exercises 25-32, simplify the logarithmic...Ch. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - For Exercises 49-52, write the logarithm as a sum...Ch. 3 - Prob. 50RECh. 3 - For Exercises 49-52, write the logarithm as a sum...Ch. 3 - Prob. 52RECh. 3 - For Exercises 53-55, write the logarithmic...Ch. 3 - For Exercises 53-55, write the logarithmic...Ch. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - For Exercises 56-58, use...Ch. 3 - For Exercises 56-58, use...Ch. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - For Exercises 61-80, solve the equation. Write the...Ch. 3 - For Exercises 61-80, solve the equation. Write the...Ch. 3 - For Exercises 61-80, solve the equation. Write the...Ch. 3 - For Exercises 61-80, solve the equation. Write the...Ch. 3 - For Exercises 61-80, solve the equation. Write the...Ch. 3 - For Exercises 61-80, solve the equation. Write the...Ch. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - The percentage of visible light P (in decimal...Ch. 3 - For Exercises 84-85, solve for the indicated...Ch. 3 - For Exercises 84-85, solve for the indicated...Ch. 3 - Prob. 86RECh. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - Prob. 89RECh. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Given fx=4x31, a. Write an equation for f1x. b....Ch. 3 - Prob. 2TCh. 3 - Prob. 3TCh. 3 - For Exercises 4-7, a. Write the domain and range...Ch. 3 - Prob. 5TCh. 3 - For Exercises 4-7, a. Write the domain and range...Ch. 3 - For Exercises 4-7, a. Write the domain and range...Ch. 3 - For Exercises 8-11, a. Graph the function. b....Ch. 3 - For Exercises 8-11, a. Graph the function. b....Ch. 3 - For Exercises 8-11, a. Graph the function. b....Ch. 3 - For Exercises 8-11, a. Graph the function. b....Ch. 3 - Write the statement in exponential form. lnx+y=aCh. 3 - Prob. 13TCh. 3 - Prob. 14TCh. 3 - For Exercises 13-18, evaluate the logarithmic...Ch. 3 - Prob. 16TCh. 3 - Prob. 17TCh. 3 - Prob. 18TCh. 3 - Prob. 19TCh. 3 - Prob. 20TCh. 3 - Prob. 21TCh. 3 - Prob. 22TCh. 3 - For Exercises 23-24, write the logarithmic...Ch. 3 - Prob. 24TCh. 3 - Prob. 25TCh. 3 - Prob. 26TCh. 3 - Prob. 27TCh. 3 - Prob. 28TCh. 3 - Prob. 29TCh. 3 - Prob. 30TCh. 3 - Prob. 31TCh. 3 - Prob. 32TCh. 3 - For Exercises 27-36, solve the equation. Write the...Ch. 3 - Prob. 34TCh. 3 - Prob. 35TCh. 3 - Prob. 36TCh. 3 - Prob. 37TCh. 3 - For Exercises 37-38, solve for the indicated...Ch. 3 - Suppose that $10,000 is invested and the account...Ch. 3 - Prob. 40TCh. 3 - The population Pt of a herd of deer on an island...Ch. 3 - The number N of visitors to a new website is given...Ch. 3 - Prob. 1CRECh. 3 - For Exercises 1-2, simplify the expression. 52x23Ch. 3 - Prob. 3CRECh. 3 - Prob. 4CRECh. 3 - For Exercises 5-13, solve the equations and...Ch. 3 - Prob. 6CRECh. 3 - Prob. 7CRECh. 3 - Prob. 8CRECh. 3 - Prob. 9CRECh. 3 - Prob. 10CRECh. 3 - Prob. 11CRECh. 3 - Prob. 12CRECh. 3 - Prob. 13CRECh. 3 - Prob. 14CRECh. 3 - Prob. 15CRECh. 3 - Prob. 16CRECh. 3 - Given fx=3x+6x2, a. Write an equation of the...Ch. 3 - Prob. 18CRECh. 3 - Prob. 19CRECh. 3 - Prob. 20CRE
Additional Math Textbook Solutions
Find more solutions based on key concepts
Explain why commands and questions are not statements.
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Draining a tank An inverted conical water tank with a height of 12 ft and a radius of 6 ft is drained through a...
Calculus: Early Transcendentals (2nd Edition)
CHECK POINT 1 Find a counterexample to show that the statement The product of two two-digit numbers is a three-...
Thinking Mathematically (6th Edition)
3. Measures of Center In what sense are the mean, median, mode, and midrange measures of “center”?
Elementary Statistics (13th Edition)
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- The graph of f(x) is given in the figure below. draw tangent lines to the graph at x=-3,x=-2,x=1,and x=4. estimate f'(-3),f'(-2),f'(1),and f'(4). Round your answers to one decimal place.arrow_forwardConsider the functions f(x)=4x-1 and g(x)=sq root of -x+7. Determine 1. f o g(x) 2. Give the domain of f o g(x) 3. g o f (x) 4. Give the domain of g o f(x)arrow_forward12. lim h→0 √5x+5h -√5x h where x>0 is constaarrow_forward
- Example 1 Solve the following differential equations: dy dx ex = 3x²-6x+5 dy dx = 4, y(0) = 3 x dy dx 33 = 5x3 +4 Prof. Robdera 5 -10:54 1x ㅁ +arrow_forward21. First-Order Constant-Coefficient Equations. a. Substituting y = ert, find the auxiliary equation for the first-order linear equation ay+by = 0, where a and b are constants with a 0. b. Use the result of part (a) to find the general solution.arrow_forwardLet f be a function whose graph consists of 5 line segments and a semicircle as shown in the figure below. Let g(x) = √ƒƒ(t) dt . 0 3 2 -2 2 4 5 6 7 8 9 10 11 12 13 14 15 1. g(0) = 2. g(2) = 3. g(4) = 4. g(6) = 5. g'(3) = 6. g'(13)=arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY