Chapter 3.4, Problem 45E

End of the Earth In 5 billion year the Sun will have run out of hydrogen fuel and begin to expand into a red giant, eventually engulfing the Earth and causing it to spiral into the core of the Sun 7.5 billion years from now. The following graph⁵⁰ shows the expanding radius of the red giant Sun (in red) and the radius of the Earth’s orbit about the Sun (in green) during its final three and a half million years of existence. The radii are measured in astronomical units (AU; one AU is the current radius of the Earth’s orbit around the Sun, approximately 93 million miles), and time is measured in millions of years.

r (AU)

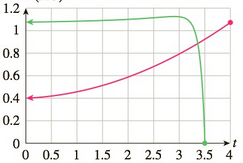
The curve representing the Sun’s radius has equation

$r=0.037t^2+0.02t+\mathrm{0.4.}$

( $t=4$ marks the end of the red giant expansion phase.) Exercises 45and 46are based on this curve.

a. Calculate the rate of change of the radius of the Sun over the successive intervals $\left[0,1\right],\left[1,2\right],\left[2,3\right],\left[3,4\right]$.

b. The successive rates of change are a linear function of t. What is the slope of that linear function? How fast will the rate of change of the Sun’s radius be increasing in the final 4 million years?