
You may wish to review Sections 16.4 and 16.8 on the transport of energy by string waves and sound. Figure P33.46 is a graphical representation of an
Figure P33.46
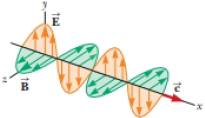
(a)
To draw: The sketch a graph of the electric field at the instant
Answer to Problem 34.70AP
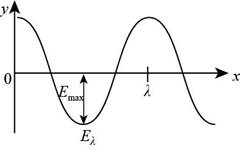
Figure (1)
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
Introduction: The electric filed is a region around a charged particle within which a force would be experienced by other particles that may be attractive force or repulsive force.
Explanation:
The electric field in the figure is perpendicular to the magnetic field and the sinusoidal wave is travelling with the speed of light. The waves move on the positive x axis and the electric field is in the
The expression for the electric field is,
Here,
Substitute
The diagram of the electric field is shown below.
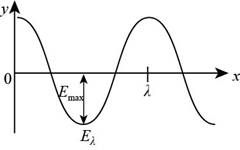
Figure (1)
(b)
Answer to Problem 34.70AP
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The formula to calculate the energy density in the electric field is,
Here,
Substitute
Thus, the energy density
Conclusion:
Therefore, the energy density
(c)
Answer to Problem 34.70AP
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The expression for the magnetic field is,
Here,
Substitute
The formula to calculate the energy density in the magnetic is,
Here,
Substitute
Thus, the energy density
Conclusion:
Therefore, the energy density
(d)
Answer to Problem 34.70AP
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The expression for the energy due to magnetic field at instant
The value of
Substitute
The formula to calculate the total energy density is,
Substitute
Thus, the total energy density in terms of electric field amplitude is
Conclusion:
Therefore, the total energy density in terms of electric field amplitude is
(e)
Answer to Problem 34.70AP
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The expression for the energy in the shoebox is,
Here,
Substitute
Integrate the above equation to find the value of
Thus, the amount of energy in the shoebox is
Conclusion:
Therefore, the amount of energy in the shoebox is
(f)
Answer to Problem 34.70AP
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The expression for the energy in the shoebox is,
The formula to calculate the power is,
Substitute
Thus, the power the wave carries through area
Conclusion:
Therefore, the power the wave carries through area
(g)
Answer to Problem 34.70AP
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The formula to calculate the intensity of the wave is,
Substitute
Thus, the intensity of the wave is
Conclusion:
Therefore, the intensity of the wave is
(h)
Answer to Problem 34.70AP
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The formula to calculate the average intensity is,
Substitute the average value as
Thus, the average value of the intensity is same as that given in the equation.
Conclusion:
Therefore, the expression of the result is same as that of the expression.
Want to see more full solutions like this?
Chapter 34 Solutions
Physics for Scientists and Engineers (AP Edition)
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





