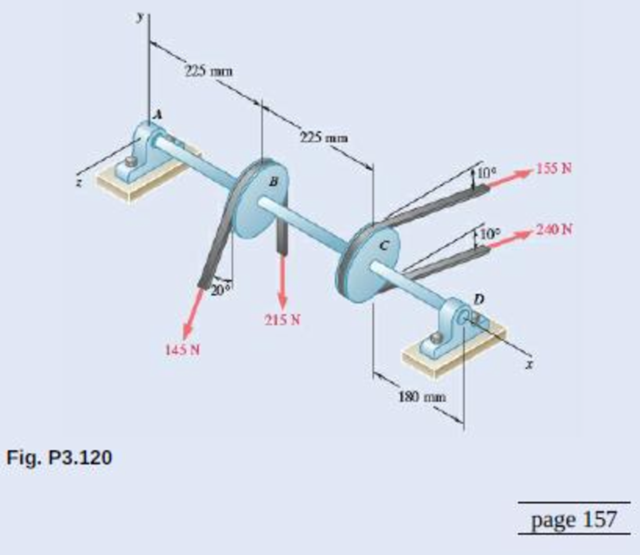
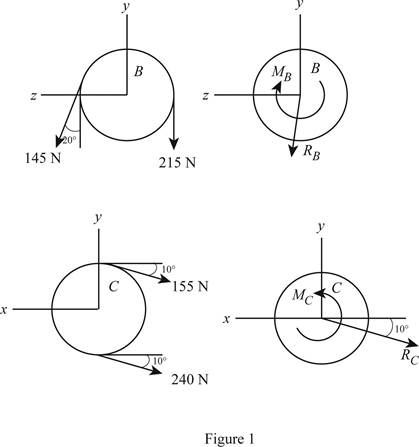
Refer Fig P3.120. Its vector diagrams showing equivalent force-couple is given below.
Write the formula to calculate the resultant force pulley B.
R→B=F→B1+F→B2 (I)
Here, R→B is the resultant force on pulley B, F→B1 and F→B2 are the forces acting on pulley B.
Write the formula to calculate the net moment of couple on pulley B.
MB=rb(−FB1+FB2)i^ (II)
Here, MB is moment of resultant couple about pulley B, FB1 and FB2 are the magnitudes of forces on pulley B, and rb is the radius of pulley B.
Write the formula to calculate the resultant force pulley C.
R→C=F→C1+F→C2 (III)
Here, R→C is the resultant force on pulley C, F→C1 and F→C2 are the forces acting on pulley C.
Write the formula to calculate the net moment of couple on pulley B.
MC=rc(FC2−FC1)i^ (IV)
Here, MC is moment of resultant couple about pulley C, FC1 and FC2 are the magnitudes of forces on pulley B, and rc is the radius of pulley C.
Write the expression to calculate the net force on pulley.
R→=R→B+R→C (V)
Here, R→ is the resultant force vector of whole system.
Write the expression to calculate the resultant moment of couple about point A.
MA=M→B+M→C+(r→B/A×R→B)+(r→C/A×R→C) (VI)
Here, MA is the net moment of couple of system about point A, rB/A is the distance between end A to pulley B, and rC/A is the distance between pulley C and end A.
Write the determinant form to calculate r×F.
r×F=|ijkrirjrkFiFjFk| (VII)
Here, ri is the component of r in x-direction, rj is the component of r in y-direction, rk is the is the component of r in z-direction, Fi is the component of F in x-direction, Fj is the component of F in y-direction, and Fk is the component of F in z-direction.
Conclusion:
Substitute (−145 N)[cos 20°+sin20°k⌢]j^ for F→B1, (−215 N)j^ for F→B2 in equation (I) to find R→B.
R→B=(−145 N)[cos 20°j^+sin20°k⌢]+(−215 N)j^=(−351.26 N)j^+(49.59 N)k⌢
Substitute 215 N for FB2, 145 N for FB1, and 75 mm for rb in equation (II) to find MB.
MB=(75 mm(1 m103 mm))(−215 N+145 N)i^=(−5.25 N⋅m)i^
Substitute (155 N)[−sin 10°j^−cos10°k⌢] for F→C1 and (240 N)[−sin 10°j^−cos10°k⌢] for F→C2 in equation (III) to find R→C.
R→C=(155 N)[−sin 10°j^−cos10°k⌢]+(240 N)[−sin 10°j^−cos10°k⌢]=(−68.59 N)j^−(389.00 N)k^
Substitute 240 N for FC2, 155 N for FC1, and 75 mm for rc in equation (IV) to find MC.
MC=(75 mm(1 m103 mm))(240 N−155 N)i^=(6.375 N⋅m)i^
Substitute (−351.26 N)j^+(49.59 N)k⌢ for R→B and (−68.59 N)j^−(389.00 N)k^ for R→C in equation (V) to find R→.
R→=[(−351.26 N)j^+(49.59 N)k^]+[(−68.59 N)j^−(389.00 N)k^]=(420 N)j^−(339 N)k^
Substitute (−5.25 N⋅m)i^ for MB, (6.375 N⋅m)i^ for MC, (225 mm)i^ for rB/A, (−351.26 N)j^+(49.59 N)k⌢ for R→B, (450 mm)i^ for r→C/A, (−68.59 N)j^−(389.00 N)k^ for R→C in equation (VI) to find MA.
MA={(−5.25 N⋅m)i^+(6.375 N⋅m)i^+((225 mm)i^×[(−351.26 N)j^+(49.59 N)k^])+((450 mm)i^×[(−68.59 N)j^−(389.00 N)k^])} (IIX)
Calculate (225 mm)i^×[(−351.26 N)j^+(49.59 N)k^] using equation (VII).
(225 mm)i^×[(−351.26 N)j^+(49.59 N)k^]=|i^j^k^225 mm(1 m103 mm)0 m0 m0 N−351.26 N49.59 N|=−(11.16 N⋅m)j^−(79.03 N⋅m)k^ (IX)
Calculate (450 mm)i^×[(−68.59 N)j^−(389.00 N)k^] using equation (VII).
(450 mm)i^×[(−68.59 N)j^−(389.00 N)k^]=|i^j^k^450 mm(1 m103 mm)0 m0 m0 N−68.59 N−389.00 N|=(−175.05 N⋅m)j^ (X)
Rewrite equation (IIX) by substituting equations (IX) and (X).
MA=(−5.25 N⋅m)i^+(6.375 N⋅m)i^+[−(11.16 N⋅m)j^−(79.03 N⋅m)k^]+(−175.05 N⋅m)j^=(1.125 N⋅m)i^+(163.9 N⋅m)j^−(109.9 N⋅m)k^
Therefore, the equivalent force is (420 N)j^−(339 N)k⌢ and resultant moment of couple about point A is (1.125 N⋅m)i^+(163.9 N⋅m)j^−(109.9 N⋅m)k^.