Student Solutions Manual For Zill's A First Course In Differential Equations With Modeling Applications, 11th
11th Edition
ISBN: 9781305965737
Author: Dennis G. Zill
Publisher: Brooks Cole
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.3, Problem 8E
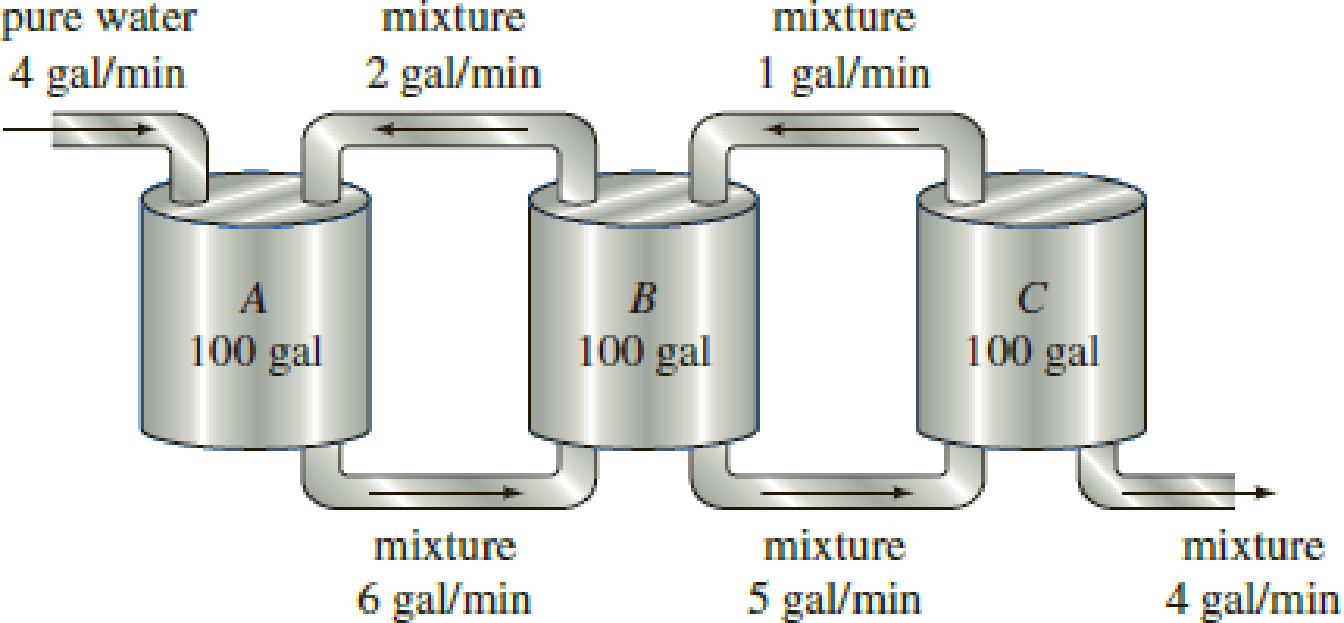
Use the information given in Figure 3.3.6 to construct a mathematical model for the number of pounds of salt x1(t), x2(t), and x3(t) at time t in tanks A, B, and C, respectively.
FIGURE 3.3.6 Mixing tanks in Problem 8
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Explain the key points and reasons for the establishment of 12.3.2(integral Test)
Use identity (1+x+x2+...+xn)*(1-x)=1-xn+1 to derive the result of 12.2.2. Please notice that identity doesn't work when x=1.
Explain the key points and reasons for the establishment of 11.3.2(integral Test)
Chapter 3 Solutions
Student Solutions Manual For Zill's A First Course In Differential Equations With Modeling Applications, 11th
Ch. 3.1 - The population of a community is known to increase...Ch. 3.1 - Suppose it is known that the population of the...Ch. 3.1 - The population of a town grows at a rate...Ch. 3.1 - The population of bacteria in a culture grows at a...Ch. 3.1 - The radioactive isotope of lead, Pb-209, decays at...Ch. 3.1 - Initially 100 milligrams of a radioactive...Ch. 3.1 - Determine the half-life of the radioactive...Ch. 3.1 - Consider the initial-value problem dA/dt = kA,...Ch. 3.1 - When a vertical beam of light passes through a...Ch. 3.1 - When interest is compounded continuously, the...
Ch. 3.1 - Carbon Dating Archaeologists used pieces of burned...Ch. 3.1 - The Shroud of Turin, which shows the negative...Ch. 3.1 - Newtons Law of Cooling/Warming A thermometer is...Ch. 3.1 - A thermometer is taken from an inside room to the...Ch. 3.1 - A small metal bar, whose initial temperature was...Ch. 3.1 - Two large containers A and B of the same size are...Ch. 3.1 - A thermometer reading 70 F is placed in an oven...Ch. 3.1 - At t = 0 a sealed test tube containing a chemical...Ch. 3.1 - A dead body was found within a closed room of a...Ch. 3.1 - The rate at which a body cools also depends on its...Ch. 3.1 - A tank contains 200 liters of fluid in which 30...Ch. 3.1 - Solve Problem 21 assuming that pure water is...Ch. 3.1 - A large tank is filled to capacity with 500...Ch. 3.1 - In Problem 23, what is the concentration c(t) of...Ch. 3.1 - Solve Problem 23 under the assumption that the...Ch. 3.1 - Determine the amount of salt in the tank at time t...Ch. 3.1 - A large tank is partially filled with 100 gallons...Ch. 3.1 - In Example 5 the size of the tank containing the...Ch. 3.1 - A 30-volt electromotive force is applied to an...Ch. 3.1 - Prob. 30ECh. 3.1 - A 100-volt electromotive force is applied to an...Ch. 3.1 - A 200-volt electromotive force is applied to an...Ch. 3.1 - An electromotive force E(t)={120,0t200,t20 is...Ch. 3.1 - An LR-series circuit has a variable inductor with...Ch. 3.1 - Air Resistance In (14) of Section 1.3 we saw that...Ch. 3.1 - How High?No Air Resistance Suppose a small...Ch. 3.1 - How High?Linear Air Resistance Repeat Problem 36,...Ch. 3.1 - Skydiving A skydiver weighs 125 pounds, and her...Ch. 3.1 - Rocket Motion Suppose a small single-stage rocket...Ch. 3.1 - Rocket MotionContinued In Problem 39 suppose of...Ch. 3.1 - Evaporating Raindrop As a raindrop falls, it...Ch. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Constant-Harvest model A model that describes the...Ch. 3.1 - Drug Dissemination A mathematical model for the...Ch. 3.1 - Memorization When forgetfulness is taken into...Ch. 3.1 - Heart Pacemaker A heart pacemaker, shown in Figure...Ch. 3.1 - Sliding Box (a) A box of mass m slides down an...Ch. 3.1 - Sliding Box—Continued
In Problem 48 let s(t) be...Ch. 3.1 - What Goes Up (a) It is well known that the model...Ch. 3.2 - The number N(t) of supermarkets throughout the...Ch. 3.2 - The number N(t) of people in a community who are...Ch. 3.2 - A model for the population P(t) in a suburb of a...Ch. 3.2 - Census data for the United States between 1790 and...Ch. 3.2 - (a) If a constant number h of fish are harvested...Ch. 3.2 - Investigate the harvesting model in Problem 5 both...Ch. 3.2 - Repeat Problem 6 in the case a = 5, b = 1, h = 7.Ch. 3.2 - (a) Suppose a = b = 1 in the Gompertz differential...Ch. 3.2 - Two chemicals A and B are combined to form a...Ch. 3.2 - Solve Problem 9 if 100 grams of chemical A is...Ch. 3.2 - Leaking cylindrical tank A tank in the form of a...Ch. 3.2 - Leaking cylindrical tank—continued When friction...Ch. 3.2 - Leaking Conical Tank A tank in the form of a...Ch. 3.2 - Inverted Conical Tank Suppose that the conical...Ch. 3.2 - Air Resistance A differential equation for the...Ch. 3.2 - How High?Nonlinear Air Resistance Consider the...Ch. 3.2 - That Sinking Feeling (a) Determine a differential...Ch. 3.2 - Solar Collector The differential equation...Ch. 3.2 - Tsunami (a) A simple model for the shape of a...Ch. 3.2 - Evaporation An outdoor decorative pond in the...Ch. 3.2 - Doomsday equation Consider the differential...Ch. 3.2 - Doomsday or extinction Suppose the population...Ch. 3.2 - Skydiving A skydiver is equipped with a stopwatch...Ch. 3.2 - Prob. 27ECh. 3.2 - Old Man River In Figure 3.2.8(a) suppose that the...Ch. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Time Drips By The clepsydra, or water clock, was a...Ch. 3.2 - (a) Suppose that a glass tank has the shape of a...Ch. 3.2 - Prob. 35ECh. 3.3 - We have not discussed methods by which systems of...Ch. 3.3 - In Problem 1 suppose that time is measured in...Ch. 3.3 - Use the graphs in Problem 2 to approximate the...Ch. 3.3 - Construct a mathematical model for a radioactive...Ch. 3.3 - Potassium-40 Decay The chemical element potassium...Ch. 3.3 - Potassium-Argon Dating The knowledge of how K-40...Ch. 3.3 - Consider two tanks A and B, with liquid being...Ch. 3.3 - Use the information given in Figure 3.3.6 to...Ch. 3.3 - Two very large tanks A and B are each partially...Ch. 3.3 - Three large tanks contain brine, as shown in...Ch. 3.3 - Consider the Lotka-Volterra predator-prey model...Ch. 3.3 - Show that a system of differential equations that...Ch. 3.3 - Determine a system of first-order differential...Ch. 3.3 - Prob. 16ECh. 3.3 - SIR Model A communicable disease is spread...Ch. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Mixtures Solely on the basis of the physical...Ch. 3.3 - Newtons Law of Cooling/Warming As shown in Figure...Ch. 3 - Answer Problems 1 and 2 without referring back to...Ch. 3 - Answer Problems 1 and 2 without referring back to...Ch. 3 - Prob. 3RECh. 3 - Air containing 0.06% carbon dioxide is pumped into...Ch. 3 - tzi the Iceman In September of 1991 two German...Ch. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Suppose a cell is suspended in a solution...Ch. 3 - Suppose that as a body cools, the temperature of...Ch. 3 - According to Stefans law of radiation the absolute...Ch. 3 - Suppose an RC-series circuit has a variable...Ch. 3 - A classical problem in the calculus of variations...Ch. 3 - A model for the populations of two interacting...Ch. 3 - Initially, two large tanks A and B each hold 100...Ch. 3 - Prob. 15RECh. 3 - When all the curves in a family G(x, y, c1) = 0...Ch. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Sawing Wood A long uniform piece of wood (cross...Ch. 3 - Solve the initial-value problem in Problem 20 when...Ch. 3 - Prob. 22RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- To explain how to view "Infinite Series" from "Infinite Sequence"’s perspective, refer to 12.2.1arrow_forwardExplain the key points and reasons for the establishment of 12.2.5 and 12.2.6arrow_forwardPage < 1 of 2 - ZOOM + 1) a) Find a matrix P such that PT AP orthogonally diagonalizes the following matrix A. = [{² 1] A = b) Verify that PT AP gives the correct diagonal form. 2 01 -2 3 2) Given the following matrices A = -1 0 1] an and B = 0 1 -3 2 find the following matrices: a) (AB) b) (BA)T 3) Find the inverse of the following matrix A using Gauss-Jordan elimination or adjoint of the matrix and check the correctness of your answer (Hint: AA¯¹ = I). [1 1 1 A = 3 5 4 L3 6 5 4) Solve the following system of linear equations using any one of Cramer's Rule, Gaussian Elimination, Gauss-Jordan Elimination or Inverse Matrix methods and check the correctness of your answer. 4x-y-z=1 2x + 2y + 3z = 10 5x-2y-2z = -1 5) a) Describe the zero vector and the additive inverse of a vector in the vector space, M3,3. b) Determine if the following set S is a subspace of M3,3 with the standard operations. Show all appropriate supporting work.arrow_forward
- 13) Let U = {j, k, l, m, n, o, p} be the universal set. Let V = {m, o,p), W = {l,o, k}, and X = {j,k). List the elements of the following sets and the cardinal number of each set. a) W° and n(W) b) (VUW) and n((V U W)') c) VUWUX and n(V U W UX) d) vnWnX and n(V WnX)arrow_forward9) Use the Venn Diagram given below to determine the number elements in each of the following sets. a) n(A). b) n(A° UBC). U B oh a k gy ท W z r e t ་ Carrow_forward10) Find n(K) given that n(T) = 7,n(KT) = 5,n(KUT) = 13.arrow_forward
- 7) Use the Venn Diagram below to determine the sets A, B, and U. A = B = U = Blue Orange white Yellow Black Pink Purple green Grey brown Uarrow_forward8. For x>_1, the continuous function g is decreasing and positive. A portion of the graph of g is shown above. For n>_1, the nth term of the series summation from n=1 to infinity a_n is defined by a_n=g(n). If intergral 1 to infinity g(x)dx converges to 8, which of the following could be true? A) summation n=1 to infinity a_n = 6. B) summation n=1 to infinity a_n =8. C) summation n=1 to infinity a_n = 10. D) summation n=1 to infinity a_n diverges.arrow_forward8) Use the Venn diagram provided to shade An Bº. A B U Darrow_forward
- 5) Describe the difference between disjoint sets and overlapping sets.arrow_forward12) Suppose U = {a,b,c,d,e) and A = {a, b, c, e) and B = (c,d,e). Determine (An B).arrow_forward1) Use the roster method to list the elements of the set consisting of: a) All positive multiples of 3 that are less than 20. b) Nothing (An empty set).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
UG/ linear equation in linear algebra; Author: The Gate Academy;https://www.youtube.com/watch?v=aN5ezoOXX5A;License: Standard YouTube License, CC-BY
System of Linear Equations-I; Author: IIT Roorkee July 2018;https://www.youtube.com/watch?v=HOXWRNuH3BE;License: Standard YouTube License, CC-BY