WEBASSIGN F/EPPS DISCRETE MATHEMATICS
5th Edition
ISBN: 9780357540244
Author: EPP
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3.3, Problem 46ES
In 46—54, refer to the Tarski world given in Figure 3.1.1, which is shown again here for reference. The domains of all variables consist of all the objects in the Tarski world. For each statement, (a) indicate whether the statement is true or false and justify your answer, (b) write the given statement using the formal logical notation illustrated in Example 3.3.10, and (c) write a negation for the given statement using the formal logical notation of Example 3.3.10.
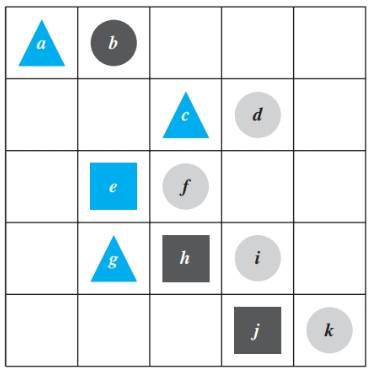
There is a triangle x such that for every square y, x is above y.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Can you answer this question for me
Use mathematical induction to prove the following statement: For all natural numbers n, 5 divides 6^n - 1 (show every step in detail)
Solve this
Chapter 3 Solutions
WEBASSIGN F/EPPS DISCRETE MATHEMATICS
Ch. 3.1 - If P(x) is a predicate with domain D, the truth...Ch. 3.1 - Some ways to express the symbol in words are .Ch. 3.1 - Some ways to express the symbol in words are .Ch. 3.1 - A statement of from xD , Q(x) is true if, and only...Ch. 3.1 - A statement of the form xD such that Q(x) is true:...Ch. 3.1 - A menagerie consists of seven brown dogs, two...Ch. 3.1 - Indicate which of the following statements are...Ch. 3.1 - Let R(m,n) be the predicate “If m is a factor if...Ch. 3.1 - Let Q(x,y) be the predicate “If xy then x2y2 ”...Ch. 3.1 - Find the truth set of each predicate. Predicate:...
Ch. 3.1 - Let B(x) be “ 10x10 .” Find the truth set of B(x)...Ch. 3.1 - Let S be the set of all strings of length 3...Ch. 3.1 - Let T be the set of all strings of length 3...Ch. 3.1 - Find counterexamples to show that the statements...Ch. 3.1 - Find counterexamples to show that the statements...Ch. 3.1 - Find counterexamples to show that the statements...Ch. 3.1 - Find counterexamples to show that the statements...Ch. 3.1 - Consider the following statement: basketball...Ch. 3.1 - Consider the following statement: xR such that...Ch. 3.1 - Rewrite the following statements informally in at...Ch. 3.1 - Rewrite each of the following statements in the...Ch. 3.1 - Rewrite each of the following in the form “ _____...Ch. 3.1 - Let D be the sat of all students at your school,...Ch. 3.1 - Consider the following statement: integer n, if...Ch. 3.1 - Rewrite the following statement informally in at...Ch. 3.1 - Prob. 21ESCh. 3.1 - Rewrite each of the following statements in the...Ch. 3.1 - Rewrite each of the following statements in the...Ch. 3.1 - Rewrite the following statements in the two forms...Ch. 3.1 - The statement “The square of any rational number...Ch. 3.1 - Consider the statement “All integers are rational...Ch. 3.1 - Refer to the picture of Tarski’s world given in...Ch. 3.1 - In 28-30, rewrite each statement without using...Ch. 3.1 - Let the domain of x be the set of geometric...Ch. 3.1 - Let the domain of x be Z, the set of integers, and...Ch. 3.1 - In any mathematics or computer science text other...Ch. 3.1 - Let R be the domain of the predicate variable x....Ch. 3.1 - Prob. 33ESCh. 3.2 - A negation for “All R have property S” is “There...Ch. 3.2 - A negation for “Some R have property S” is...Ch. 3.2 - A negation for “For every x, if x has property P...Ch. 3.2 - The converse of “For every x, if x has property P...Ch. 3.2 - The contrapositive of “For every x, if x has...Ch. 3.2 - The inverse of “For every x, if x has property P...Ch. 3.2 - Which of the following is a negation for “All...Ch. 3.2 - Which of the following is a negation for “All dogs...Ch. 3.2 - Write a formula negation for each of the following...Ch. 3.2 - Write an informal negation for each of the...Ch. 3.2 - Write a negation for each of the following...Ch. 3.2 - Write a negation for each statement in 6 and 7....Ch. 3.2 - Write a negation for each statement in 6 and 7....Ch. 3.2 - Consider the statement “There are no simple...Ch. 3.2 - Write negation for each statement in 9 and 10. ...Ch. 3.2 - Write a negation for each statements in 9 and 10. ...Ch. 3.2 - In each of 11-14 determine whether the proposed...Ch. 3.2 - In each of 11-14 determine whether the proposed...Ch. 3.2 - Prob. 13ESCh. 3.2 - Prob. 14ESCh. 3.2 - Prob. 15ESCh. 3.2 - In 16-23, write a negation for each statement. ...Ch. 3.2 - In 16-23, write a negation for each statement. ...Ch. 3.2 - Prob. 18ESCh. 3.2 - In 16-23, write a negation for each statement. nZ...Ch. 3.2 - Prob. 20ESCh. 3.2 - Prob. 21ESCh. 3.2 - In 16-23, write a negation for each statement. If...Ch. 3.2 - In 16-23, write a negation for each statement. If...Ch. 3.2 - Prob. 24ESCh. 3.2 - Prob. 25ESCh. 3.2 - In 26-33, for each statement in the referenced...Ch. 3.2 - In 26-33, for each statement in the referenced...Ch. 3.2 - Prob. 28ESCh. 3.2 - In 26-33, for each statement in the referenced...Ch. 3.2 - Prob. 30ESCh. 3.2 - In 26-33, for each statement in the referenced...Ch. 3.2 - In 26-33, for each statement in the referenced...Ch. 3.2 - In 26-33, for each statement in the referenced...Ch. 3.2 - Prob. 34ESCh. 3.2 - Give an example to show that a universal condition...Ch. 3.2 - If P(x) is a predicate and the domain of x is the...Ch. 3.2 - Consider the following sequence of digits: 0204. A...Ch. 3.2 - True or false? All occurrences of the letter u in...Ch. 3.2 - Prob. 39ESCh. 3.2 - Rewrite each statement of 39-44 if-then form....Ch. 3.2 - Rewrite each statement of 39-44 if-then form....Ch. 3.2 - Rewrite each statement of 39-44 if-then form....Ch. 3.2 - Rewrite each statement of 39-44 in if-then form. A...Ch. 3.2 - Rewrite each statement of 39-44 in if-then form. A...Ch. 3.2 - Prob. 45ESCh. 3.2 - Use the facts that the negation of a STATEMENT IS...Ch. 3.2 - Prob. 47ESCh. 3.2 - Use the facts that the negation of STATEMENT IS A...Ch. 3.2 - The computer scientist Richard Conway and David...Ch. 3.2 - A frequent-flyer club brochure stares, “you may...Ch. 3.3 - To establish the truth of a statement of the form...Ch. 3.3 - Prob. 2TYCh. 3.3 - Prob. 3TYCh. 3.3 - Consider the statement “ x such that y , P(x,y), a...Ch. 3.3 - Prob. 5TYCh. 3.3 - Prob. 1ESCh. 3.3 - Let G(x,y) be “ x2y .” Indicate which of the...Ch. 3.3 - The following statement is true: “ nonzero number...Ch. 3.3 - The following statement is true: “ real number x,...Ch. 3.3 - Prob. 5ESCh. 3.3 - The statements in exercise 5-8 refer to the Tarski...Ch. 3.3 - Prob. 7ESCh. 3.3 - This statements is exercised 5-8 refer to the...Ch. 3.3 - Prob. 9ESCh. 3.3 - This exercise refers to Example 3.3.3. Determine...Ch. 3.3 - Let Sbe the set of students at your school, let M...Ch. 3.3 - Let D = E ={-2,-1,0,1,2}. Write negations for each...Ch. 3.3 - Prob. 13ESCh. 3.3 - Prob. 14ESCh. 3.3 - Prob. 15ESCh. 3.3 - Prob. 16ESCh. 3.3 - Prob. 17ESCh. 3.3 - Prob. 18ESCh. 3.3 - Prob. 19ESCh. 3.3 - Recall that reversing that order of the...Ch. 3.3 - For each of following equators, determinewhich of...Ch. 3.3 - Prob. 22ESCh. 3.3 - In 22 and 23, rewrite each statement without using...Ch. 3.3 - Prob. 24ESCh. 3.3 - Each statement in 25—28 refers to Tarski world of...Ch. 3.3 - Each statement in 25—28 refers to Tarski world of...Ch. 3.3 - Prob. 27ESCh. 3.3 - Prob. 28ESCh. 3.3 - Prob. 29ESCh. 3.3 - Prob. 30ESCh. 3.3 - Prob. 31ESCh. 3.3 - Prob. 32ESCh. 3.3 - Prob. 33ESCh. 3.3 - In 33-39(a) rewrite the statement formally using...Ch. 3.3 - In 33-39(a) rewrite the statement formally using...Ch. 3.3 - In 33-39(a) rewrite the statement formally using...Ch. 3.3 - In 33-39(a) rewrite the statement formally using...Ch. 3.3 - In 33-39(a) rewrite the statement formally using...Ch. 3.3 - Prob. 39ESCh. 3.3 - Prob. 40ESCh. 3.3 - Indicate which of the following statements are...Ch. 3.3 - Write the negation of the definition of limit of a...Ch. 3.3 - The following is the definition for limxaf(x)=L ....Ch. 3.3 - The notation ! stands for the words “There exists...Ch. 3.3 - Suppose that P(x) is a predicate and D is the...Ch. 3.3 - In 46—54, refer to the Tarski world given in...Ch. 3.3 - Prob. 47ESCh. 3.3 - Prob. 48ESCh. 3.3 - In 46—54, refer to the Tarski world given in...Ch. 3.3 - In 46—54, refer to the Tarski world given in...Ch. 3.3 - Y13In 46—54, refer to the Tarski world given in...Ch. 3.3 - Prob. 52ESCh. 3.3 - Prob. 53ESCh. 3.3 - Prob. 54ESCh. 3.3 - Let P(x)and Q(x) be predicates and suppose D is...Ch. 3.3 - Let P(x) and Q(x) be predicates and suppose D is...Ch. 3.3 - Let P(x) and Q(x) be predicates and suppose D is...Ch. 3.3 - Let P(x) and Q(x) be predicates and suppose D is...Ch. 3.3 - Prob. 59ESCh. 3.3 - In 59-61, find the answers Prolog would give if...Ch. 3.3 - Prob. 61ESCh. 3.4 - The rule of universal instantiation says that if...Ch. 3.4 - If the first two premises of universal modus...Ch. 3.4 - Prob. 3TYCh. 3.4 - If the first two premised of universal...Ch. 3.4 - Prob. 5TYCh. 3.4 - Prob. 1ESCh. 3.4 - Prob. 2ESCh. 3.4 - Prob. 3ESCh. 3.4 - real numbers r, a, and b, if b, if r is positive,...Ch. 3.4 - Prob. 5ESCh. 3.4 - Prob. 6ESCh. 3.4 - Some of the arguments in 7-18 are valid by...Ch. 3.4 - Prob. 8ESCh. 3.4 - Prob. 9ESCh. 3.4 - Prob. 10ESCh. 3.4 - Some of the arguments in 7—18 are valid by...Ch. 3.4 - Some of the arguments in 7—18 are valid by...Ch. 3.4 - Some of the arguments in 7-18 are valid by...Ch. 3.4 - Some of the arguments in 7-18 are valid by...Ch. 3.4 - Some of the arguments in 7-18 are valid by...Ch. 3.4 - Some of the arguments in 7-18 are valid by...Ch. 3.4 - Prob. 17ESCh. 3.4 - Some of the arguments in 7-18 are valid by...Ch. 3.4 - Rewrite the statement “No good cars are cheap” in...Ch. 3.4 - Use a diagram to shoe that the following argument...Ch. 3.4 - Indicate whether the arguments in 21-27 are valid...Ch. 3.4 - Indicate whether the arguments in 21-27 are valid...Ch. 3.4 - Prob. 23ESCh. 3.4 - Indicate whether the arguments in 21-27 are valid...Ch. 3.4 - Prob. 25ESCh. 3.4 - Prob. 26ESCh. 3.4 - Prob. 27ESCh. 3.4 - In exercises 28-32, reorder the premises in each...Ch. 3.4 - In exercises 28-32, reorder the premises in each...Ch. 3.4 - In exercises 28-32, reorder the premises in each...Ch. 3.4 - Prob. 31ESCh. 3.4 - In exercises 28-32, reorder the premises in each...Ch. 3.4 - Prob. 33ESCh. 3.4 - In 33 and 34 a single conclusion follows when all...Ch. 3.4 - Prob. 35ESCh. 3.4 - Derives the validity of universal form of part(a)...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Use mathematical induction to prove the following statement: For all natural numbers n, 5 divides 6^n - 1arrow_forwardthe set of all preimages of 2 isarrow_forwardWhich diagram(s) represent the following relationships An injective function from A to B? A surjective function from A to B? An injective function from B to A? A surjective function from B to A?arrow_forward
- int/PlayerHomework.aspx?homeworkId=689099898&questionId=1&flushed=false&cid=8120746¢erw BP Physical Geograph... HW Score: 0%, 0 of 13 points ○ Points: 0 of 1 Determine if the values of the variables listed are solutions of the system of equations. 2x - y = 4 3x+5y= - 6 x=1, y = 2; (1,-2) Is (1, 2) a solution of the system of equations? L No Yes iew an example Get more help - Aarrow_forwardDetermine if each statement is true or false. If the statement is false, provide a brief explanation: a) There exists x = R such that √x2 = -x. b) Let A = {x = ZIx = 1 (mod 3)} and B = {x = ZIx is odd}. Then A and B are disjoint. c) Let A and B be subsets of a universal set U. If x = A and x/ € A - B,then x = An B.| E d) Let f : RR be defined by f (x) = 1 x + 2 1. Then f is surjective.arrow_forwardWrite the negation of the definition of an injective functionarrow_forward
- Let U= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {xeU Ix is a multiple of 3}, and B = {x = UIx = 0 (mod 2)}. Use the roster method to list all elements in each of the following sets: a) A, b) B, c) A u B, d) B – A, e) A^cn Barrow_forwardThe function f is; Injective (only), Surjective (only), Bijective, or none? show workarrow_forwardFor each a Є Z, if a ‡0 (mod 3), then a² = 1 (mod 3).arrow_forward
- find: f(3)=? , and the set of all preimages of 2 is ?arrow_forward12:01 PM Tue May 13 < AA ✓ Educatic S s3.amazona... A Assess Your... 目 accelerate-iu15-bssd.vschool.com S s3.amazona... Trigonometric Identities Module Exam Dashboard ... Dashboard ... Algebra 2 Pa... Algebra 2 Part 4 [Honors] (Acc. Ed.) (Zimmerman) 24-25 / Module 11: Trigonometric Identities i + 38% ✰ Start Page Alexis Forsythe All changes saved 10. A sound wave's amplitude can be modeled by the function y = −7 sin ((x-1) + 4). Within the interval 0 < x < 12, when does the function have an amplitude of 4? (Select all that apply.) 9.522 seconds 4.199 seconds 0.522 seconds 1.199 seconds Previous 10 of 20 Nextarrow_forwardTechniques QUAT6221 2025 PT B... TM Tabudi Maphoru Activities Assessments Class Progress lIE Library • Help v The table below shows the prices (R) and quantities (kg) of rice, meat and potatoes items bought during 2013 and 2014: 2013 2014 P1Qo PoQo Q1Po P1Q1 Price Ро Quantity Qo Price P1 Quantity Q1 Rice 7 80 6 70 480 560 490 420 Meat 30 50 35 60 1 750 1 500 1 800 2 100 Potatoes 3 100 3 100 300 300 300 300 TOTAL 40 230 44 230 2 530 2 360 2 590 2 820 Instructions: 1 Corall dawn to tha bottom of thir ceraan urina se se tha haca nariad in archerca antarand cubmit Q Search ENG US 口X 2025/05arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elements Of Modern Algebra
Algebra
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Propositional Logic, Propositional Variables & Compound Propositions; Author: Neso Academy;https://www.youtube.com/watch?v=Ib5njCwNMdk;License: Standard YouTube License, CC-BY
Propositional Logic - Discrete math; Author: Charles Edeki - Math Computer Science Programming;https://www.youtube.com/watch?v=rL_8y2v1Guw;License: Standard YouTube License, CC-BY
DM-12-Propositional Logic-Basics; Author: GATEBOOK VIDEO LECTURES;https://www.youtube.com/watch?v=pzUBrJLIESU;License: Standard Youtube License
Lecture 1 - Propositional Logic; Author: nptelhrd;https://www.youtube.com/watch?v=xlUFkMKSB3Y;License: Standard YouTube License, CC-BY
MFCS unit-1 || Part:1 || JNTU || Well formed formula || propositional calculus || truth tables; Author: Learn with Smily;https://www.youtube.com/watch?v=XV15Q4mCcHc;License: Standard YouTube License, CC-BY