
The magnitude of the couple (M) and direction of its axis after replacing two couples in to single equivalent couple.
Answer to Problem 3.79P
The magnitude of the couple (M) and direction of its axis
Explanation of Solution
Given information:
The two vertical forces
The inclined force acting at point B
The inclined force acting at point C
The force acting at the point E
The force acting at the point D
The height between point C and F (CF) is 120 mm.
The height between point F and A (FA) is 120 mm.
The horizontal distance between point E and D (ED) is 192 mm.
The height between point E and B (EB) is 144 mm.
The distance between point C and D (CD) is 160 mm.
Calculation:
Replace the couple in the ABCD plane with two couple’s P and Q.
Draw the couple ABCD by replacing with two couple’s P and Q as in Figure (1).
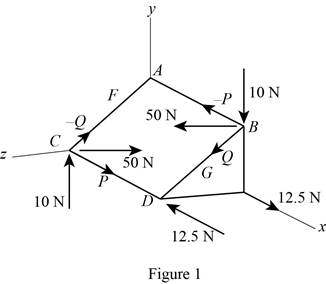
Calculate the distance CG using the Pythagoras theorem:
Substitute 160 mm for CD and 120 mm for CF.
Calculate the force (P) acting at the point B using the formula:
Substitute 50 N for
Calculate the force (Q) acting at the point C using the formula:
Substitute 50 N for
Calculate the angle
Substitute 144 mm for EB and 192 mm for ED.
Calculate the couple vector
Substitute 40 N for P, 120 mm for CF, 120 mm for FA, 30 N for Q, and 160 mm for CD.
Write the couple vector
Substitute
Calculate the couple vector
Substitute 12.5 N for
Write the couple vector
Calculate the position vector of BC
Substitute 160 mm for CD, 144 mm for EB, and 192 mm for ED.
Calculate the couple vector
Substitute
Calculate magnitude of the couple (M) using the relation:
Substitute
Calculate the direction of axis along x direction
Substitute
Calculate the direction of axis along y direction
Substitute
Calculate the direction of axis along z direction
Substitute
Thus, the magnitude of the couple (M) and direction of its axis
Want to see more full solutions like this?
Chapter 3 Solutions
VECTOR MECH...,STAT.+DYNA.(LL)-W/ACCESS
- I need to find m in R = mD from the image given. Do you really need to know what R and D is to find R. I was thinking geometrically we can find a relationship between R and D. D = R*cos(30). Then R = mD becomes m = R/D = 1/cos(30) = 1.1547. Is that correct?arrow_forwardQ1] B/ (16 Marks) To produce a lightweight epoxy part to provide thermal insulation. The available material are hollow glass beads for which the outside diameter is 1.6 mm and the wall thickness is 0.04 mm. Determine the weight and number of beads that must be added to the epoxy to produce a 0.5 kg of composite with a density of 0.65 g/cm³. The density of the glass is 2.5 g/cm³ and that of the epoxy is 1.25 g/cm³.arrow_forwardBelow is a projection of the inertia ellipsoid in the b1-b2 plane (b1 and b2 are unit vectors). All points on the ellipsoid surface represent moments of inertia in various directions. The distance R is related to the distance D such that R = md. Determine m.arrow_forward
- Below is a projection of the inertia ellipsoid in the b1-b2 plane (b1 and b2 are unit vectors). All points on the ellipsoid surface represent moments of inertia in various directions. Determine I_aa ( moment of inertia) for direction n_a (this is a unit vector).arrow_forwardThe problems are generally based on the following model: A particular spacecraft can be represented as a single axisymmetric rigid body B. Let n₂ be inertially fixed unit vectors; then, 6, are parallel to central, principal axes. To make the mathematics simpler, introduce a frame C where n₂ = ĉ₁ = b; initially. 6₁ Assume a mass distribution such that J =₁₁• B* •b₁ = 450 kg - m² I = b² •Ï¾˜ • b₂ = b¸ •Ï¾* •b¸ = 200 kg - m² K J-I C³ =r₁₁ = r₁₁arrow_forwardThe problems are generally based on the following model: A particular spacecraft can be represented as a single axisymmetric rigid body B. Let n₂ be inertially fixed unit vectors; then, 6, are parallel to central, principal axes. To make the mathematics simpler, introduce a frame C where n₂ = ĉ₁ = b; initially. 6₁ Assume a mass distribution such that J =₁₁• B* •b₁ = 450 kg - m² I = b² •Ï¾˜ • b₂ = b¸ •Ï¾* •b¸ = 200 kg - m² K J-I C³ =r₁₁ = r₁₁arrow_forward
- The problems are generally based on the following model: A particular spacecraft can be represented as a single axisymmetric rigid body B. Let n₂ be inertially fixed unit vectors; then, 6, are parallel to central, principal axes. To make the mathematics simpler, introduce a frame C where n₂ = ĉ₁ = b; initially. 6₁ Assume a mass distribution such that J =₁₁• B* •b₁ = 450 kg - m² I = b² •Ï¾˜ • b₂ = b¸ •Ï¾* •b¸ = 200 kg - m² K J-I C³ =r₁₁ = r₁₁arrow_forward##### Determine an example of a design of a compressed air system, which uses the criterion of speed for the design of the pipes (formula attached). The demands of flow rate, power as well as air velocity in the pipelines can be freely chosen. Sizing the compressor (flow, power...) Size reservoir required Setting the dryer Determine the amount of water withdrawn from the system due to air compression **With the attached formula you can choose the appropriate values of the unknownsarrow_forwardTo make an introduction to a report of a simple design of a compressed air system, which uses the criterion of speed, and not that of pressure drop, to determine the diameter of the pipes, where the capacity of the compressor and the demands of the equipment are expressed in flow.arrow_forward
- In an irrigation system, the following characteristics of the pipe network are available.• 100 meters of 4" PVC pipe, 3 gate valves• 500 meters of 3" PVC pipe, 4 gate valves• 200 meters of 2" H.G. pipe, 2 globe valves• 50 litres per second circulate in the pipes:Calculate:1. Total energy losses in meters.2. Leaks in pipes.3. Losses in accessories.4. Calculate the equivalent pipe of that system assuming only pipes without fittings.Solve the problem without artificial intelligence, solve by one of the expertsarrow_forwardLiquid water enters the boiler at 60 bar. Steam exits the boiler at 60 bar, 540°C and undergoes a throttling process to 40 bar before entering the turbine. Steam expands adiabatically through the turbine to 5 bar, 240°C, and then undergoes a throttling process to 1 bar before entering the condenser. Kinetic and potential energy effects can be ignored. Draw a Temperature-Entropy diagram and mark each of the states 2-5 on this diagram. Determine the power generated by the turbine, in kJ per kg of steam flowing. For the valves and the turbine, evaluate the rate of entropy production, each in kJ/K per kg of steam flowing.arrow_forwardFind the componenets of reactions at pins of A, B and D please show the detailed process and instructions for learning draw out all diagrams please and thank youarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





