Calculus: Single And Multivariable, 7e Student Solutions Manual
Calculus: Single And Multivariable, 7e Student Solutions Manual
7th Edition
ISBN: 9781119138549
Author: Deborah Hughes-Hallett, William G. McCallum, Andrew M. Gleason, Daniel E. Flath, Patti Frazer Lock, Sheldon P. Gordon, David O. Lomen, David Lovelock, Brad G. Osgood, Andrew Pasquale, Douglas Quinney, Jeff Tecosky-Feldman, Joseph Thrash, Karen R. Rhea, Thomas W. Tucker
Publisher: WILEY
bartleby

Concept explainers

Rate of Change
The relation between two quantities which displays how much greater one quantity is than another is called ratio.
Slope
The change in the vertical distances is known as the rise and the change in the horizontal distances is known as the run. So, the rise divided by run is nothing but a slope value. It is calculated with simple algebraic equations as:
bartleby

Videos

Textbook Question
Book Icon
Chapter 3.3, Problem 34E

For Problems 34–39, let h ( x ) = f ( x ) ⋅ g ( x ) , and k ( x ) = f ( x ) / g ( x ) , and l ( x ) = g ( x ) / f ( x ) . Use Figure 3.15 to estimate the derivatives.

Chapter 3.3, Problem 34E, For Problems 3439, let h(x)=f(x)g(x), and k(x)=f(x)/g(x), and l(x)=g(x)/f(x). Use Figure 3.15 to

Figure 3.15

h ′ ( 1 )

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 3.3, Problem 33E
Next
Chapter 3.3, Problem 35E
Students have asked these similar questions
I need help in ensuring that I explain it propleryy in the simplifest way as possible
I need help making sure that I explain this part accutartly.
Please help me with this question as I want to know how can I perform the partial fraction decompostion on this alebgric equation to find the time-domain of y(t)

Chapter 3 Solutions

Calculus: Single And Multivariable, 7e Student Solutions Manual

Ch. 3.1 - Let f(x) = 7. Using the denition of the...Ch. 3.1 - Let f(x) = 17x+11. Use the denition of the...Ch. 3.1 - For Exercises 35, determine if the derivative...Ch. 3.1 - For Exercises 35, determine if the derivative...Ch. 3.1 - For Exercises 35, determine if the derivative...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...
Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - For Exercises 649, find the derivatives of the...Ch. 3.1 - In Exercises 5057, use the tangent line...Ch. 3.1 - In Exercises 5057, use the tangent line...Ch. 3.1 - In Exercises 5057, use the tangent line...Ch. 3.1 - In Exercises 5057, use the tangent line...Ch. 3.1 - In Exercises 5057, use the tangent line...Ch. 3.1 - In Exercises 5057, use the tangent line...Ch. 3.1 - In Exercises 5057, use the tangent line...Ch. 3.1 - In Exercises 5057, use the tangent line...Ch. 3.1 - If f(x)=6x42x+7, find f(x), f(x), and f(x).Ch. 3.1 - (a) Let f(x) = x7. Find f(x), f(x), and f(x). (b)...Ch. 3.1 - If p(t)=t3+2t2t+4, find d2p/dt2 and d3p/dt3.Ch. 3.1 - If w(x)=x+(1/x), find d2w/dx2 and d3w/dx3.Ch. 3.1 - For Problems 6267, determine if the derivative...Ch. 3.1 - For Problems 6267, determine if the derivative...Ch. 3.1 - For Problems 6267, determine if the derivative...Ch. 3.1 - For Problems 6267, determine if the derivative...Ch. 3.1 - For Problems 6267, determine if the derivative...Ch. 3.1 - For Problems 6267, determine if the derivative...Ch. 3.1 - If f(x)=(3x+8)(2x5), find f(x) and f(x).Ch. 3.1 - Find the equation of the line tangent to the graph...Ch. 3.1 - Find the equation of the line tangent to y=x2+3x5...Ch. 3.1 - Find the equation of the line tangent to f(x) at x...Ch. 3.1 - (a) Find the equation of the tangent line to f(x)...Ch. 3.1 - (a) Use Figure 3.8 to rank the quantities f (1), f...Ch. 3.1 - The graph of y=x39x216x+1 has a slope of 5 at two...Ch. 3.1 - On what intervals is the graph of f(x)=x44x3 both...Ch. 3.1 - For what values of x is the function y=x55x both...Ch. 3.1 - (a) Find the eighth derivative of...Ch. 3.1 - For the functions in Problems 7881: (a) Find the...Ch. 3.1 - For the functions in Problems 7881: (a) Find the...Ch. 3.1 - For the functions in Problems 7881: (a) Find the...Ch. 3.1 - For the functions in Problems 7881: (a) Find the...Ch. 3.1 - With t in years since 2016, the height of a sand...Ch. 3.1 - A rubber balloon contains neon. As the air...Ch. 3.1 - A ball is dropped from the top of the Empire State...Ch. 3.1 - At a time t seconds after it is thrown up in the...Ch. 3.1 - Let f(t) and g(t) give, respectively, the amount...Ch. 3.1 - A jkulhlaup is the rapid draining of a glacial...Ch. 3.1 - (a) For y = kxn, show that near any point x = a,...Ch. 3.1 - In Problems 8992, use the fact that for a power...Ch. 3.1 - In Problems 8992, use the fact that for a power...Ch. 3.1 - In Problems 8992, use the fact that for a power...Ch. 3.1 - In Problems 8992, use the fact that for a power...Ch. 3.1 - The depth, h (in mm), of the water runoff down a...Ch. 3.1 - If M is the mass of the earth and G is a constant,...Ch. 3.1 - The period, T, of a pendulum is given in terms of...Ch. 3.1 - (a) Use the formula for the area of a circle of...Ch. 3.1 - Show that for any power function f(x) = xn, we...Ch. 3.1 - Suppose W is proportional to r3. The derivative...Ch. 3.1 - Given a power function of the form f(x) = axn,...Ch. 3.1 - (a) Find the value of a making f(x) continuous at...Ch. 3.1 - Let f(x)=x3+3x22x+1 and g(x)=x3+3x22x4. (a) Show...Ch. 3.1 - Let f(x)=x43x2+1. (a) Show that f(x) is an even...Ch. 3.1 - In Problems 103104, explain what is wrong with the...Ch. 3.1 - In Problems 103104, explain what is wrong with the...Ch. 3.1 - In Problems 105107, give an example of: Two...Ch. 3.1 - In Problems 105107, give an example of: A function...Ch. 3.1 - In Problems 105107, give an example of: A function...Ch. 3.1 - In Problems 108110, is the statement true or...Ch. 3.1 - In Problems 108110, is the statement true or...Ch. 3.1 - In Problems 108110, is the statement true or...Ch. 3.1 - In Problems 111112, is the statement true or...Ch. 3.1 - In Problems 111112, is the statement true or...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 125, find the derivatives of the...Ch. 3.2 - In Exercises 2628, find formulas for f and f....Ch. 3.2 - In Exercises 2628, find formulas for f and f....Ch. 3.2 - In Exercises 2628, find formulas for f and f....Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - In Problems 2939, can the functions be...Ch. 3.2 - (a) Use Figure 3.12 to rank the quantities f (1),...Ch. 3.2 - An animal population is given by P(t) =...Ch. 3.2 - With a yearly inflation rate of 2%, prices are...Ch. 3.2 - After a storm, a high-pressure system moves into...Ch. 3.2 - The value of an automobile purchased in 2014 can...Ch. 3.2 - With t in years since the start of 2014, worldwide...Ch. 3.2 - Food bank usage in Britain has grown dramatically...Ch. 3.2 - In 2012, the population of Mexico was 115 million...Ch. 3.2 - Some antique furniture increased very rapidly in...Ch. 3.2 - Find the quadratic polynomial g(x)=ax2+bx+c which...Ch. 3.2 - In Problems 5051, explain what is wrong with the...Ch. 3.2 - In Problems 5051, explain what is wrong with the...Ch. 3.2 - In Problems 5253, give an example of: An...Ch. 3.2 - In Problems 5253, give an example of: A function f...Ch. 3.2 - Are the statements in Problems 5456 true or false?...Ch. 3.2 - Are the statements in Problems 5456 true or false?...Ch. 3.2 - Are the statements in Problems 5456 true or false?...Ch. 3.3 - If f(x)=x2(x3+5), find f(x) two ways: by using the...Ch. 3.3 - If f(x)=2x3x, find f(x) two ways: by using the...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - For Exercises 330, find the derivative. It may be...Ch. 3.3 - In Problems 3133, use Figure 3.14 and the product...Ch. 3.3 - In Problems 3133, use Figure 3.14 and the product...Ch. 3.3 - In Problems 3133, use Figure 3.14 and the product...Ch. 3.3 - For Problems 3439, let h(x)=f(x)g(x), and...Ch. 3.3 - For Problems 3439, let h(x)=f(x)g(x), and...Ch. 3.3 - For Problems 3439, let h(x)=f(x)g(x), and...Ch. 3.3 - For Problems 3439, let h(x)=f(x)g(x), and...Ch. 3.3 - For Problems 3439, let h(x)=f(x)g(x), and...Ch. 3.3 - For Problems 3439, let h(x)=f(x)g(x), and...Ch. 3.3 - Differentiate f(t)=et by writing it as f(t)=1et.Ch. 3.3 - Differentiate f(x)=e2x by writing it as f(x)=exex.Ch. 3.3 - Differentiate f(x)=e3x by writing it as f(x)=exe2x...Ch. 3.3 - For what intervals is f(x)=xex concave up?Ch. 3.3 - For what intervals is g(x)=1x2+1 concave down?Ch. 3.3 - Find the equation of the tangent line to the graph...Ch. 3.3 - Find the equation of the tangent line to the graph...Ch. 3.3 - Find the equation of the tangent line to the graph...Ch. 3.3 - In Problems 4851, the functions f(x), g(x), and...Ch. 3.3 - In Problems 4851, the functions f(x), g(x), and...Ch. 3.3 - In Problems 4851, the functions f(x), g(x), and...Ch. 3.3 - In Problems 4851, the functions f(x), g(x), and...Ch. 3.3 - The differentiable functions f and g have the...Ch. 3.3 - If H (3) = 1, H (3) = 3, F(3) = 5, F (3) = 4,...Ch. 3.3 - Find the slope of the line tangent to...Ch. 3.3 - Find a possible formula for a function y = f(x)...Ch. 3.3 - The density of veins on leaves tells us about a...Ch. 3.3 - The quantity, q, of a skateboard sold depends on...Ch. 3.3 - A museum has decided to sell one of its paintings...Ch. 3.3 - Let f() be the gas consumption (in liters/km) of a...Ch. 3.3 - The manager of a political campaign uses two...Ch. 3.3 - A mutual fund holds N(t) million shares of a...Ch. 3.3 - A patients total cholesterol level, T (t), and...Ch. 3.3 - For Problems 6366, use the graphs of h(x) and g(x)...Ch. 3.3 - For Problems 6366, use the graphs of h(x) and g(x)...Ch. 3.3 - For Problems 6366, use the graphs of h(x) and g(x)...Ch. 3.3 - For Problems 6366, use the graphs of h(x) and g(x)...Ch. 3.3 - In Problems 6769, explain what is wrong with the...Ch. 3.3 - In Problems 6769, explain what is wrong with the...Ch. 3.3 - In Problems 6769, explain what is wrong with the...Ch. 3.3 - In Problems 7071, give an example of: A function...Ch. 3.3 - In Problems 7071, give an example of: A function...Ch. 3.3 - Are the statements in Problems 7274 true or false?...Ch. 3.3 - Are the statements in Problems 7274 true or false?...Ch. 3.3 - Are the statements in Problems 7274 true or false?...Ch. 3.3 - Which of the following would be a counterexample...Ch. 3.3 - In Problems 7679, let f(x) = g(x)h(x), with g (2)...Ch. 3.3 - In Problems 7679, let f(x) = g(x)h(x), with g(2) =...Ch. 3.3 - In Problems 7679, let f(x) = g(x)h(x), with g (2)...Ch. 3.3 - In Problems 7679, let f(x) = g(x)h(x), with g (2)...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Exercises 157, find the derivatives. Assume...Ch. 3.4 - In Problems 5861, use Figure 3.16 and the chain...Ch. 3.4 - In Problems 5861, use Figure 3.16 and the chain...Ch. 3.4 - In Problems 5861, use Figure 3.16 and the chain...Ch. 3.4 - In Problems 5861, use Figure 3.16 and the chain...Ch. 3.4 - In Problems 6265, use Figure 3.17 to evaluate the...Ch. 3.4 - In Problems 6265, use Figure 3.17 to evaluate the...Ch. 3.4 - In Problems 6265, use Figure 3.17 to evaluate the...Ch. 3.4 - In Problems 6265, use Figure 3.17 to evaluate the...Ch. 3.4 - Find the equation of the tangent line to f(x) = (x...Ch. 3.4 - Find the equation of the line tangent to y = f(x)...Ch. 3.4 - Find the equation of the line tangent to f(t) =...Ch. 3.4 - For what values of x is the graph of y=ex2 concave...Ch. 3.4 - For what intervals is f(x)=xex concave down?Ch. 3.4 - Suppose f(x)=(2x+1)10(3x1)7. Find a formula for f...Ch. 3.4 - Find a possible formula for a function m(x) such...Ch. 3.4 - Given F(2) = 1, F(2) = 5, F(4) = 3, F(4) = 7 and...Ch. 3.4 - Given f(x) with f(1) = 2 and f (1) = 5, find (a)...Ch. 3.4 - Given f(x) with f(2) = 7 and f (2) = 3 and f (4) =...Ch. 3.4 - A particle is moving on the x-axis, where x is in...Ch. 3.4 - A fish population is approximated by P(t)=10e0.6t,...Ch. 3.4 - The worlds population8 is about f(t)=7.17e0.011t...Ch. 3.4 - Fourth-quarter net sales for the Hershey Company9,...Ch. 3.4 - For t in years since 2010, daily oil consumption...Ch. 3.4 - The balance in a bank account t years after money...Ch. 3.4 - For t 0 in minutes, the temperature, H, of a pot...Ch. 3.4 - A yam is put in a hot oven, maintained at a...Ch. 3.4 - The 2010 census12 determined the population of the...Ch. 3.4 - If you invest P dollars in a bank account at an...Ch. 3.4 - The theory of relativity predicts that an object...Ch. 3.4 - Since the 1950s, the carbon dioxide concentration...Ch. 3.4 - Instruments on a plane measure the distance...Ch. 3.4 - For Problems 8992, if f(x) has a positive slope...Ch. 3.4 - For Problems 8992, if f(x) has a positive slope...Ch. 3.4 - For Problems 8992, if f(x) has a positive slope...Ch. 3.4 - For Problems 8992, if f(x) has a positive slope...Ch. 3.4 - In Problems 9395, explain what is wrong with the...Ch. 3.4 - In Problems 9395, explain what is wrong with the...Ch. 3.4 - In Problems 9395, explain what is wrong with the...Ch. 3.4 - In Problems 9697, give an example of: A function...Ch. 3.4 - In Problems 9697, give an example of: A function...Ch. 3.4 - Are the statements in Problems 98101 true or...Ch. 3.4 - Are the statements in Problems 98101 true or...Ch. 3.4 - Are the statements in Problems 98101 true or...Ch. 3.4 - Are the statements in Problems 98101 true or...Ch. 3.5 - Construct a table of values for cos x, x = 0, 0.1,...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - Prob. 35ECh. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Exercises 249, find the derivatives of the...Ch. 3.5 - In Problems 5052, find formulas for f and f....Ch. 3.5 - In Problems 5052, find formulas for f and f....Ch. 3.5 - In Problems 5052, find formulas for f and f....Ch. 3.5 - Is the graph of y = sin(x4) increasing or...Ch. 3.5 - Find the line tangent to f(t)=3sin(2t)+5 at the...Ch. 3.5 - Find the line tangent to f(x)=3x+cos(5x) at the...Ch. 3.5 - Find the line tangent to f(t)=8+sin(3t) at the...Ch. 3.5 - Find the 50th derivative of y = cos x.Ch. 3.5 - Find a function F(x) satisfying F (x) = sin(4x).Ch. 3.5 - Let f(x)=sin2x+cos2x. (a) Find f(x) using the...Ch. 3.5 - On page 42 the depth, y, in feet, of water in...Ch. 3.5 - A boat at anchor is bobbing up and down in the...Ch. 3.5 - The voltage, V, in volts, in an electrical outlet...Ch. 3.5 - An oscillating mass of m gm at the end of a spring...Ch. 3.5 - With t in years, the population of a herd of deer...Ch. 3.5 - An environmentalist reports that the depth of the...Ch. 3.5 - Normal human body temperature fluctuates with a...Ch. 3.5 - In Problems 6770, find and interpret the value of...Ch. 3.5 - In Problems 6770, find and interpret the value of...Ch. 3.5 - In Problems 6770, find and interpret the value of...Ch. 3.5 - Prob. 70ECh. 3.5 - A rubber duck bounces up and down in a pool after...Ch. 3.5 - The metal bar of length l in Figure 3.23 has one...Ch. 3.5 - Let f(x) = ex sin x. (a) Find the derivative f(x)....Ch. 3.5 - In Problems 7475, explain what is wrong with the...Ch. 3.5 - In Problems 7475, explain what is wrong with the...Ch. 3.5 - In Problems 7677, give an example of: A...Ch. 3.5 - In Problems 7677, give an example of: A function...Ch. 3.5 - Are the statements in Problems 7880 true or false?...Ch. 3.5 - Are the statements in Problems 7880 true or false?...Ch. 3.5 - Are the statements in Problems 7880 true or false?...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - For Exercises 141, find the derivative. It may be...Ch. 3.6 - Let f(x) = ln(3x). (a) Find f(x) and simplify your...Ch. 3.6 - On what intervals is ln(x2 + 1) concave up?Ch. 3.6 - Use the chain rule to obtain the formula for...Ch. 3.6 - Using the chain rule, find ddx(logx). (Recall log...Ch. 3.6 - To compare the acidity of different solutions,...Ch. 3.6 - The number of years, T, it takes an investment of...Ch. 3.6 - A firm estimates that the total revenue, R, in...Ch. 3.6 - Average leaf width, w (in mm), in tropical...Ch. 3.6 - (a) Find the equation of the tangent line to y =...Ch. 3.6 - (a) For x 0, find and simplify the derivative of...Ch. 3.6 - (a) Given that f(x) = x3, find f(2). (b) Find...Ch. 3.6 - (a) For f(x) = 2x5 + 3x3 + x, find f(x). (b) How...Ch. 3.6 - Imagine you are zooming in on the graph of each of...Ch. 3.6 - In Problems 5558, use Figure 3.25 to find a point...Ch. 3.6 - In Problems 5558, use Figure 3.25 to find a point...Ch. 3.6 - In Problems 5558, use Figure 3.25 to find a point...Ch. 3.6 - In Problems 5558, use Figure 3.25 to find a point...Ch. 3.6 - In Problems 5961, use Figure 3.26 to estimate the...Ch. 3.6 - In Problems 5961, use Figure 3.26 to estimate the...Ch. 3.6 - In Problems 5961, use Figure 3.26 to estimate the...Ch. 3.6 - In Problems 6264, use Figure 3.27 to calculate the...Ch. 3.6 - In Problems 6264, use Figure 3.27 to calculate the...Ch. 3.6 - In Problems 6264, use Figure 3.27 to calculate the...Ch. 3.6 - Use the table and the fact that f(x) is invertible...Ch. 3.6 - At a particular location, f(p) is the number of...Ch. 3.6 - Let P = f(t) give the US population18 in millions...Ch. 3.6 - Figure 3.28 shows the number of motor vehicles,19...Ch. 3.6 - Using Figure 3.29, where f(2) = 2.1, f(4) = 3.0,...Ch. 3.6 - Figure 3.30 shows an invertible function f(x). (a)...Ch. 3.6 - An invertible function f(x) has values in the...Ch. 3.6 - Assuming g(x) 0, use the chain rule to explain...Ch. 3.6 - If f is continuous, invertible, and defined for...Ch. 3.6 - Suppose f(x) is an invertible function that is...Ch. 3.6 - In Problems 7577, explain what is wrong with the...Ch. 3.6 - In Problems 7577, explain what is wrong with the...Ch. 3.6 - In Problems 7577, explain what is wrong with the...Ch. 3.6 - In Problems 7881, give an example of: A function...Ch. 3.6 - In Problems 7881, give an example of: A function...Ch. 3.6 - In Problems 7881, give an example of: A function...Ch. 3.6 - In Problems 7881, give an example of: A function f...Ch. 3.6 - Are the statements in Problems 8283 true or false?...Ch. 3.6 - Are the statements in Problems 8283 true or false?...Ch. 3.7 - Let f(x) = 7. Using the definition of the...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dy/dx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - For Exercises 121, find dydx. Assume a, b, c are...Ch. 3.7 - In Exercises 2225, find the slope of the tangent...Ch. 3.7 - In Exercises 2225, find the slope of the tangent...Ch. 3.7 - In Exercises 2225, find the slope of the tangent...Ch. 3.7 - In Exercises 2225, find the slope of the tangent...Ch. 3.7 - For Exercises 2630, find the equations of the...Ch. 3.7 - For Exercises 2630, find the equations of the...Ch. 3.7 - For Exercises 2630, find the equations of the...Ch. 3.7 - For Exercises 2630, find the equations of the...Ch. 3.7 - For Exercises 2630, find the equations of the...Ch. 3.7 - (a) Find dydx given that x2 + y2 4x + 7y = 15....Ch. 3.7 - (a) Find the slope of the tangent line to the...Ch. 3.7 - (a) Find all points on y2 + xy + x2 = 1 with x =...Ch. 3.7 - Find the equations of the tangent lines at x = 2...Ch. 3.7 - (a) Find the equations of the tangent lines to the...Ch. 3.7 - Find the equation of the tangent line to the curve...Ch. 3.7 - If y = arcsin x then x = sin y. Use implicit...Ch. 3.7 - Show that the power rule for derivatives applies...Ch. 3.7 - At pressure P atmospheres, a certain fraction f of...Ch. 3.7 - For constants a, b, n, R, Van der Waals equation...Ch. 3.7 - In Problems 4142, explain what is wrong with the...Ch. 3.7 - In Problems 4142, explain what is wrong with the...Ch. 3.7 - In Problems 4344, give an example of: A formula...Ch. 3.7 - In Problems 4344, give an example of: A curve that...Ch. 3.7 - True or false? Explain your answer: If y satisfies...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - In Exercises 111, find the derivative of the...Ch. 3.8 - Show that d(sinh x)dx = cosh x.Ch. 3.8 - Show that d(sinh x)/dx = cosh xCh. 3.8 - Show that sinh(x) = sinh(x).Ch. 3.8 - In Exercises 1516, simplify the expressions....Ch. 3.8 - In Exercises 1516, simplify the expressions....Ch. 3.8 - Describe and explain the behavior of sinh x as x ...Ch. 3.8 - If x = cosh t and y = sinh t, explain why the...Ch. 3.8 - Is there an identity analogous to sin(2x) = 2 sin...Ch. 3.8 - Is there an identity analogous to cos(2x) = cos2 x...Ch. 3.8 - Prove the identities in Problems 2122. cosh(A + B)...Ch. 3.8 - Prove the identities in Problems 2122. sinh(A + B)...Ch. 3.8 - In Problems 2326, find the limit of the function...Ch. 3.8 - In Problems 2326, find the limit of the function...Ch. 3.8 - In Problems 2326, find the limit of the function...Ch. 3.8 - In Problems 2326, find the limit of the function...Ch. 3.8 - For what values of k is limxe3x cosh kx finite?Ch. 3.8 - For what values of k is limxsinhkxcosh2x finite?Ch. 3.8 - The cable between the two towers of a power line...Ch. 3.8 - The Saint Louis Arch can be approximated by using...Ch. 3.8 - (a) Using a calculator or computer, sketch the...Ch. 3.8 - The following problem is a generalization of...Ch. 3.8 - (a) Find tanh 0. (b) For what values of x is tanh...Ch. 3.8 - In Problems 3437, explain what is wrong with the...Ch. 3.8 - In Problems 3437, explain what is wrong with the...Ch. 3.8 - In Problems 3437, explain what is wrong with the...Ch. 3.8 - In Problems 3437, explain what is wrong with the...Ch. 3.8 - In Problems 3840, give an example of: A hyperbolic...Ch. 3.8 - In Problems 3840, give an example of: A value of k...Ch. 3.8 - In Problems 3840, give an example of: A function...Ch. 3.8 - Are the statements in Problems 4145 true or false?...Ch. 3.8 - Are the statements in Problems 4145 true or false?...Ch. 3.8 - Are the statements in Problems 4145 true or false?...Ch. 3.8 - Are the statements in Problems 4145 true or false?...Ch. 3.8 - Are the statements in Problems 4145 true or false?...Ch. 3.9 - Find the tangent line approximation for 1+x near x...Ch. 3.9 - What is the tangent line approximation to ex near...Ch. 3.9 - Find the tangent line approximation to 1x near x =...Ch. 3.9 - Find the local linearization of f(x) = x2 near x =...Ch. 3.9 - What is the local linearization of ex2 near x = 1?Ch. 3.9 - Show that 1 x2 is the tangent line approximation...Ch. 3.9 - Show that ex 1 x near x = 0.Ch. 3.9 - Local linearization gives values too small for the...Ch. 3.9 - Using a graph like Figure 3.37, estimate to one...Ch. 3.9 - For x near 0, local linearization gives ex 1 + x....Ch. 3.9 - (a) Find the best linear approximation, L(x), to...Ch. 3.9 - (a) Find the tangent line approximation to cos x...Ch. 3.9 - Suppose f(x) has f(50) = 99.5 and f50) = 0.2. (a)...Ch. 3.9 - The graphs in Figure 3.39 have the same window and...Ch. 3.9 - (a) Graph f(x) = x3 3x2 + 3x + 1. (b) Find and...Ch. 3.9 - (a) Show that 1+kx is the local linearization of...Ch. 3.9 - Figure 3.40 shows f(x) and its local linearization...Ch. 3.9 - In Problems 1819, the equation has a solution near...Ch. 3.9 - In Problems 1819, the equation has a solution near...Ch. 3.9 - (a) Given that f(7) = 13 and f(7) = 0.38, estimate...Ch. 3.9 - A function g has g(3) = 7 and g(3.001) g(3) =...Ch. 3.9 - (a) Explain why the following equation has a...Ch. 3.9 - The speed of sound in dry air is...Ch. 3.9 - Live phytoplankton of diameter x micrometers sink...Ch. 3.9 - The generation time for an organism is the time...Ch. 3.9 - Air pressure at sea level is 30 inches of mercury....Ch. 3.9 - On October 7, 2010, the Wall Street Journal22...Ch. 3.9 - Table 3.9 shows the water stored S(t), in...Ch. 3.9 - Small water bugs swim in groups as protection...Ch. 3.9 - If C (in units of 104 molar) is the concentration...Ch. 3.9 - Writing g for the acceleration due to gravity, the...Ch. 3.9 - Suppose now the length of the pendulum in Problem...Ch. 3.9 - Suppose f has a continuous positive second...Ch. 3.9 - Suppose f(x) is a differentiable decreasing...Ch. 3.9 - Problems 3537 investigate the motion of a...Ch. 3.9 - Problems 3537 investigate the motion of a...Ch. 3.9 - Problems 3537 investigate the motion of a...Ch. 3.9 - In Problems 3840, find the local linearization of...Ch. 3.9 - In Problems 3840, find the local linearization of...Ch. 3.9 - In Problems 3840, find the local linearization of...Ch. 3.9 - In Problems 4145, find a formula for the error...Ch. 3.9 - In Problems 4145, find a formula for the error...Ch. 3.9 - In Problems 4145, find a formula for the error...Ch. 3.9 - In Problems 4145, find a formula for the error...Ch. 3.9 - In Problems 4145, find a formula for the error...Ch. 3.9 - Multiply the local linearization of ex near x = 0...Ch. 3.9 - (a) Show that 1 x is the local linearization of...Ch. 3.9 - From the local linearizations of ex and sin x near...Ch. 3.9 - Use local linearization to derive the product...Ch. 3.9 - Derive the chain rule using local linearization....Ch. 3.9 - Consider a function f and a point a. Suppose there...Ch. 3.9 - Consider the graph of f(x) = x2 near x = 1. Find...Ch. 3.9 - In Problems 5354, explain what is wrong with the...Ch. 3.9 - In Problems 5354, explain what is wrong with the...Ch. 3.9 - In Problems 5557, give an example of: Two...Ch. 3.9 - In Problems 5557, give an example of: A...Ch. 3.9 - In Problems 5557, give an example of: A function...Ch. 3.9 - Let f be a differentiable function and let L be...Ch. 3.10 - Let f(x) = 7. Using the definition of the...Ch. 3.10 - In Exercises 15, decide if the statements are true...Ch. 3.10 - In Exercises 15, decide if the statements are true...Ch. 3.10 - In Exercises 15, decide if the statements are true...Ch. 3.10 - In Exercises 15, decide if the statements are true...Ch. 3.10 - Do the functions graphed in Exercises 69 appear to...Ch. 3.10 - Do the functions graphed in Exercises 69 appear to...Ch. 3.10 - Do the functions graphed in Exercises 69 appear to...Ch. 3.10 - Do the functions graphed in Exercises 69 appear to...Ch. 3.10 - Applying the Mean Value Theorem with a = 2, b = 7...Ch. 3.10 - Applying the Mean Value Theorem with a = 3, b = 13...Ch. 3.10 - Let p(x) = x5 +8x4 30x3 +30x2 31x+22. What is the...Ch. 3.10 - Let p(x) be a seventh-degree polynomial with 7...Ch. 3.10 - Use the Racetrack Principle and the fact that sin...Ch. 3.10 - Use the Racetrack Principle to show that ln x x1.Ch. 3.10 - Use the fact that ln x and ex are inverse...Ch. 3.10 - State a Decreasing Function Theorem, analogous to...Ch. 3.10 - Dominic drove from Phoenix to Tucson on Interstate...Ch. 3.10 - In Problems 1922, use one of the theorems in this...Ch. 3.10 - In Problems 1922, use one of the theorems in this...Ch. 3.10 - In Problems 1922, use one of the theorems in this...Ch. 3.10 - In Problems 1922, use one of the theorems in this...Ch. 3.10 - The position of a particle on the x-axis is given...Ch. 3.10 - Suppose that g and are continuous on [a, b] and...Ch. 3.10 - Deduce the Constant Function Theorem from the...Ch. 3.10 - Prove that if f (x) = g(x) for all x in (a, b),...Ch. 3.10 - Suppose that f(x) = f(x) for all x. Prove that...Ch. 3.10 - Suppose that f is continuous on [a, b] and...Ch. 3.10 - Suppose that f(x) 0 for all x in (a, b). We will...Ch. 3.10 - In Problems 3032, explain what is wrong with the...Ch. 3.10 - In Problems 3032, explain what is wrong with the...Ch. 3.10 - In Problems 3032, explain what is wrong with the...Ch. 3.10 - In Problems 3337, give an example of: An interval...Ch. 3.10 - In Problems 3337, give an example of: An interval...Ch. 3.10 - In Problems 3337, give an example of: A continuous...Ch. 3.10 - In Problems 3337, give an example of: A function f...Ch. 3.10 - In Problems 3337, give an example of: A function...Ch. 3.10 - Are the statements in Problems 3841 true or false...Ch. 3.10 - Are the statements in Problems 3841 true or false...Ch. 3.10 - Are the statements in Problems 3841 true or false...Ch. 3.10 - Are the statements in Problems 3841 true or false...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - Find derivatives for the functions in Exercises...Ch. 3 - For Exercises 7475, assume that y is a...Ch. 3 - For Exercises 7475, assume that y is a...Ch. 3 - Find the slope of the curve x2 + 3y2 = 7 at (2,...Ch. 3 - Assume y is a differentiable function of x and...Ch. 3 - Find the equations for the lines tangent to the...Ch. 3 - If f(t) = 2t3 4t2 + 3t 1, find f(t) and f(t).Ch. 3 - If f(x)=138x+2x2 and f(r) = 4, find r.Ch. 3 - If f(x) = x3 6x2 15x+20, find analytically all...Ch. 3 - For Problems 8287, use Figure 3.1. Figure 3.1 Let...Ch. 3 - For Problems 8287, use Figure 3.1. Figure 3.1 Let...Ch. 3 - For Problems 8287, use Figure 3.1. Figure 3.1 Let...Ch. 3 - For Problems 8287, use Figure 3.1. Figure 3.1...Ch. 3 - For Problems 8287, use Figure 3.1. Figure 3.1 Let...Ch. 3 - For Problems 8287, use Figure 3.1. Figure 3.1 Find...Ch. 3 - For Problems 8891, let (x) = f(g(x)) and k(x) =...Ch. 3 - For Problems 8891, let (x) = f(g(x)) and k(x) =...Ch. 3 - For Problems 8891, let (x) = f(g(x)) and k(x) =...Ch. 3 - For Problems 8891, let (x) = f(g(x)) and k(x) =...Ch. 3 - Using the information in the table about f and g,...Ch. 3 - Given: r(2) = 4, s(2) = 1, s(4) = 2, r(2) = 1,...Ch. 3 - If g(2) = 3 and g(2) = 4, find f (2) for the...Ch. 3 - For parts (a)(f) of Problem 94, determine the...Ch. 3 - Imagine you are zooming in on the graphs of the...Ch. 3 - The graphs of sin x and cos x intersect once...Ch. 3 - In Problems 9899, show that the curves meet at...Ch. 3 - In Problems 9899, show that the curves meet at...Ch. 3 - For some constant b and x 0, let y = x ln xbx....Ch. 3 - In Problems 101103, find the limit as x ....Ch. 3 - In Problems 101103, find the limit as x ....Ch. 3 - In Problems 101103, find the limit as x ....Ch. 3 - Consider the function f(x)=x. (a) Find and sketch...Ch. 3 - Figure 3.3 shows the tangent line approximation to...Ch. 3 - Global temperatures have been rising, on average,...Ch. 3 - The population of Hungary2 has been modeled by P =...Ch. 3 - Prob. 108RECh. 3 - The distance, s, of a moving body from a fixed...Ch. 3 - At any time, t, a population, P(t), is growing at...Ch. 3 - An object is oscillating at the end of a spring....Ch. 3 - The total number of people, N, who have contracted...Ch. 3 - The world population3 was 7.17 billion in July of...Ch. 3 - The acceleration due to gravity, g, is given by...Ch. 3 - Given that f and g are differentiable everywhere,...Ch. 3 - Prob. 116RECh. 3 - A particle is moving on the x-axis. It has...Ch. 3 - If f is decreasing and f(20) = 10, which of the...Ch. 3 - Find the nth derivative of the following...Ch. 3 - The derivative f gives the (absolute) rate of...Ch. 3 - The relative rate of change of a function f is...

Additional Math Textbook Solutions

Find more solutions based on key concepts
In Problems 29-42, use transformations of the graph of y= x 4 or y= x 5 to graph each function. f( x )=2 ( x+1 ...

Precalculus

A Bloomberg Businessweek subscriber study asked, In the past 12 months, when travelling for business, what type...

STATISTICS F/BUSINESS+ECONOMICS-TEXT

Explain the meaning of the term “statistically significant difference” in statistics terminology.

Intro Stats, Books a la Carte Edition (5th Edition)

Voting A random sample of likely voters showed that 49 planned to support Measure X. The margin of error is 3 p...

Introductory Statistics

Identifying Probability Distributions. In Exercises 7–14, determine whether a probability distribution is given...

Elementary Statistics (13th Edition)

Motion in the Plane In Exercises 5–8, r(t) is the position of a particle in the xy-plane at time t. Find an equ...

University Calculus: Early Transcendentals (4th Edition)

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
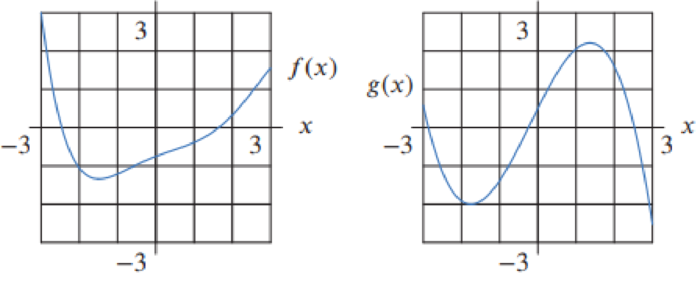
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Differential Equation | MIT 18.01SC Single Variable Calculus, Fall 2010; Author: MIT OpenCourseWare;https://www.youtube.com/watch?v=HaOHUfymsuk;License: Standard YouTube License, CC-BY