Chapter 33, Problem 17PQ

(a)

To determine

The expression for the total energy that dissipated by the resistor in one time constant.

Answer to Problem 17PQ

The expression for the total energy that dissipated by the resistor in one time constant is, $\frac{{\epsilon }^2\tau }{R}\left(\frac{2}{e}-\frac{1}{2e^2}-\frac{1}{2}\right)$.

Explanation of Solution

The following figure shows the given diagram-$33.9\text{A}$.

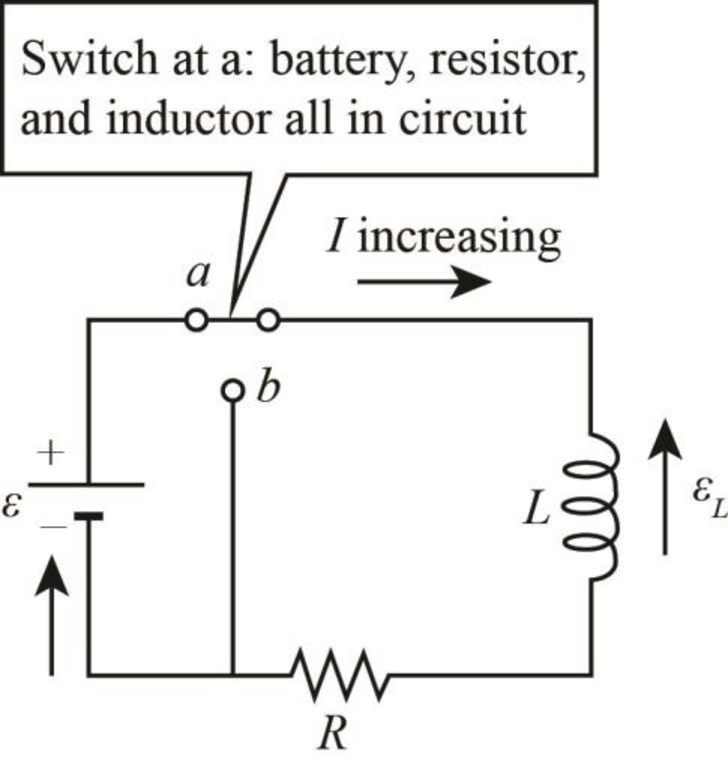
Figure-(1)

Here, $L$ is inductance, $R$ is resistance, $\epsilon$ is emf, and $I\left(t\right)$ is current as function of time.

Write the expression for current pass through the resistor.

    $I\left(t\right)=\frac{\epsilon }{R}\left(1-e^{-\frac{t}{\tau }}\right)$

Here, $t$ is time during which the current passes through the resistor, and $\tau$ is the time constant of the circuit.

Write the expression for power dissipated in the resistor as function of time.

    $P\left(t\right)=I^2\left(t\right)R$

Here, $P$ is power.

Substitute $\frac{\epsilon }{R}\left(1-e^{-\frac{t}{\tau }}\right)$ for $I\left(t\right)$ in the above equation to calculate $P\left(t\right)$.

    $\begin{array}{c}P\left(t\right)={\left[\frac{\epsilon }{R}\left(1-e^{-\frac{t}{\tau }}\right)\right]}^{2}R\\ =\frac{{\epsilon }^2}{R}{\left(1-e^{-\frac{t}{\tau }}\right)}^2\end{array}$

Write the expression for energy dissipated $\left(dU\left(t\right)\right)$ in the resistor in a small time $dt$.

    $dU\left(t\right)=P\left(t\right)dt$

Substitute $\frac{{\epsilon }^2}{R}{\left(1-e^{-\frac{t}{\tau }}\right)}^2$ for $P\left(t\right)$ in the above equation to calculate $\left(dU\left(t\right)\right)$.

    $\begin{array}{c}dU\left(t\right)=\frac{{\epsilon }^2}{R}{\left(1-e^{-\frac{t}{\tau }}\right)}^{2}dt\\ =\frac{{\epsilon }^2}{R}\left(1-2e^{-\frac{t}{\tau }}+e^{-\frac{2t}{\tau }}\right)dt\end{array}$

Integrate the above expression between the limits $0$ to $\tau$.

    $\begin{array}{c}dU\left(t\right)={\displaystyle {\int }_0^{\tau }\frac{{\epsilon }^2}{R}\left(1-2e^{-\frac{t}{\tau }}+e^{-\frac{2t}{\tau }}\right)dt}\\ =\frac{{\epsilon }^2}{R}{\left[t+2\tau e^{-\frac{t}{\tau }}-\frac{\tau }{2}{e}^{-\frac{2t}{\tau }}\right]}_0^{\tau }\\ =\frac{{\epsilon }^2}{R}\left[\left(\tau -0\right)+2\tau \left(e^{-1}-1\right)-\frac{\tau }{2}\left(e^{-2}-1\right)\right]\\ =\frac{{\epsilon }^2\tau }{R}\left(\frac{2}{e}-\frac{1}{2e^2}-\frac{1}{2}\right)\end{array}$

Conclusion:

Therefore, the expression for the total energy that dissipated by the resistor in one time constant is $\frac{{\epsilon }^2\tau }{R}\left(\frac{2}{e}-\frac{1}{2e^2}-\frac{1}{2}\right)$.

(b)

To determine

The expression for the total charge that passes through the resistor in one time constant.

Answer to Problem 17PQ

The expression for the total charge that passes through the resistor in one time constant is, $\frac{{\epsilon }^2\tau }{2R}\left(1-\frac{1}{e^2}\right)$.

Explanation of Solution

Write the expression for decaying current.

    $I\left(t\right)=\frac{\epsilon }{R}{e}^{-\frac{t}{\tau }}$

Write the expression for power dissipated in the resistor as function of time.

    $P\left(t\right)=I^2\left(t\right)R$

Substitute $\frac{\epsilon }{R}{e}^{-\frac{t}{\tau }}$ for $I\left(t\right)$ in the above equation.

    $\begin{array}{c}P\left(t\right)={\left[\frac{\epsilon }{R}{e}^{-\frac{t}{\tau }}\right]}^{2}R\\ =\frac{{\epsilon }^2}{R}{\left(e^{-\frac{t}{\tau }}\right)}^2\\ =\frac{{\epsilon }^2}{R}\left(e^{-\frac{2t}{\tau }}\right)\end{array}$

Integrate the above expression between the limits $0$ to $\tau$.

    $\begin{array}{c}dU\left(t\right)={\displaystyle {\int }_0^{\tau }\frac{{\epsilon }^2}{R}\left(e^{-\frac{2t}{\tau }}\right)dt}\\ =\frac{{\epsilon }^2}{R}{\left[-\frac{\tau }{2}{e}^{-\frac{2t}{\tau }}\right]}_0^{\tau }\\ =\frac{{\epsilon }^2}{R}\left[-\frac{\tau }{2}\left(1-e^{-2}\right)\right]\\ =\frac{{\epsilon }^2\tau }{2R}\left(1-\frac{1}{e^2}\right)\end{array}$

Conclusion:

Therefore, the expression for the total energy that dissipated by the resistor in one time constant is, $\frac{{\epsilon }^2\tau }{2R}\left(1-\frac{1}{e^2}\right)$.

(c)

To determine

The comparison between the above two results and comment.

Answer to Problem 17PQ

The energy dissipated in the resistor when the current decays is more than the energy dissipated when the current grows in the circuit.

Explanation of Solution

Write the expression for energy growth that dissipated through the resistor.

    ${\left(U\right)}_{\text{growth}}=\frac{{\epsilon }^2\tau }{R}\left(\frac{2}{e}-\frac{1}{2e^2}-\frac{1}{2}\right)$

Here, ${\left(U\right)}_{\text{growth}}$ is energy growth.

Write the expression for energy decay that dissipated through the resistor.

    ${\left(U\right)}_{\text{decay}}=\frac{{\epsilon }^2\tau }{2R}\left(1-\frac{1}{e^2}\right)$

Here, ${\left(U\right)}_{\text{decay}}$ is energy decay.

Take the ratio of both equations.

    $\begin{array}{c}\frac{{\left(U\right)}_{\text{growth}}}{{\left(U\right)}_{\text{decay}}}=\frac{\frac{{\epsilon }^2\tau }{R}\left(\frac{2}{e}-\frac{1}{2e^2}-\frac{1}{2}\right)}{\frac{{\epsilon }^2\tau }{2R}\left(1-\frac{1}{e^2}\right)}\\ =\frac{4e-1-e^2}{e^2-1}\end{array}$

Conclusion:

Substitute $2.718$ for $e$ in the above equation.

    $\begin{array}{c}\frac{{\left(U\right)}_{\text{growth}}}{{\left(U\right)}_{\text{decay}}}=\frac{\left(4\right)\left(2.718\right)-1-{\left(2.718\right)}^2}{{\left(2.718\right)}^2-1}\\ =0.39\end{array}$

Therefore, the energy dissipated in the resistor when the current decays is more than the energy dissipated when the current grows in the circuit.