Chapter 3.3, Problem 15E

Who is the king of late night TV? An Internet survey estimates that, when given a choice between David Letterman and Jay Leno, 52% of the population prefers to watch Jay Leno. Three late night TV watchers are randomly selected and asked which of the two talk show hosts they prefer.

1. a. Find the probability distribution for Y, the number of viewers in the sample who prefer Leno.
2. b. Construct a probability histogram for p(y).
3. c. What is the probability that exactly one of the three viewers prefers Leno?
4. d. What are the mean and standard deviation for Y?
5. e. What is the probability that the number of viewers favoring Leno falls within 2 standard deviations of the mean?

To determine

Find the probability distribution for Y, the number of viewers in the sample who prefer Leno.

Answer to Problem 15E

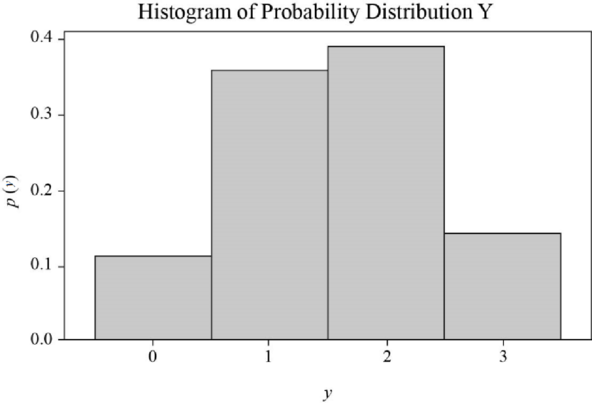
The probability distribution for Y, the number of viewers in the sample who prefer Leno is,

y	0	1	2	3
$P\left(y\right)$	0.1106	0.3594	0.3894	0.1406

Explanation of Solution

Calculation:

Define the random variable Y as number of viewers in the sample who prefer Leno is,

. The random variable Y takes values 0, 1, 2 and 3 because three late night TV watchers are selected randomly.

The probability that the population prefers to watch Jay Leno is 0.52, then the probability that the population does not prefers to watch Jay Leno is $1-0.52=0.48$.

The probability for $Y=0$ is,

$\begin{array}{c}P\left(Y=0\right)=P\left(\text{Not}\text{prefers}\right)\times P\left(\text{Not}\text{prefers}\right)\times P\left(\text{Not}\text{prefers}\right)\\ =0.48\times 0.48\times 0.48\\ =0.1106\end{array}$

The probability for $Y=1$ is,

$\begin{array}{c}P\left(Y=1\right)=\left[\begin{array}{l}P\left(\text{Prefers}\right)P\left(\text{Not}\text{prefers}\right)P\left(\text{Not}\text{prefers}\right)+\\ P\left(\text{Not}\text{prefers}\right)P\left(\text{Prefers}\right)P\left(\text{Not}\text{prefers}\right)+\\ P\left(\text{Not}\text{prefers}\right)P\left(\text{Not}\text{prefers}\right)P\left(\text{Prefers}\right)\end{array}\right]\\ =\left(0.52\times 0.48\times 0.48\right)+\left(0.48\times 0.52\times 0.48\right)+\left(0.48\times 0.48\times 0.52\right)\\ =0.1198+0.1198+0.1198\\ =0.3594\end{array}$

The probability for $Y=2$ is,

$\begin{array}{c}P\left(Y=2\right)=\left[\begin{array}{l}P\left(\text{Prefers}\right)P\left(\text{Prefers}\right)P\left(\text{Not}\text{prefers}\right)+\\ P\left(\text{Not}\text{prefers}\right)P\left(\text{Prefers}\right)P\left(\text{Prefers}\right)+\\ P\left(\text{Prefers}\right)P\left(\text{Not}\text{prefers}\right)P\left(\text{Prefers}\right)\end{array}\right]\\ =\left(0.52\times 0.52\times 0.48\right)+\left(0.48\times 0.52\times 0.52\right)+\left(0.52\times 0.48\times 0.52\right)\\ =0.1298+0.1298+0.1298\\ =0.3894\end{array}$

The probability for $Y=3$ is,

$\begin{array}{c}P\left(Y=3\right)=P\left(\text{Prefers}\right)\times P\left(\text{Prefers}\right)\times P\left(\text{Prefers}\right)\\ =0.52\times 0.52\times 0.52\\ =0.1406\end{array}$

Hence, the probability distribution for Y, the number of viewers in the sample who prefer Leno is,

y	0	1	2	3
$p\left(y\right)$	0.1106	0.3594	0.3894	0.1406

To determine

Construct a probability histogram for $p\left(y\right)$.

Answer to Problem 15E

The probability histogram is,

Explanation of Solution

Calculation:

Step by step procedure to construct histogram:

• In histogram, take the values of random variable Y on x-axis.
• Take the values of probability for random variable Y on y-axis.
• Draw a vertical bar corresponding to value 0 in x-axis with the probability value 0.1106.
• Similarly draw vertical bars for all the probability values by taking the bars side-by-side.

To determine

Find the probability that exactly one of the three viewers prefers Leno.

Answer to Problem 15E

The probability that exactly one of the three viewers prefers Leno is 0.3594.

Explanation of Solution

Calculation:

The probability that exactly one of the three viewers prefers Leno is,

$\begin{array}{c}P\left(Y=1\right)=\left[\begin{array}{l}P\left(\text{Prefers}\right)P\left(\text{Not}\text{prefers}\right)P\left(\text{Not}\text{prefers}\right)+\\ P\left(\text{Not}\text{prefers}\right)P\left(\text{Prefers}\right)P\left(\text{Not}\text{prefers}\right)+\\ P\left(\text{Not}\text{prefers}\right)P\left(\text{Not}\text{prefers}\right)P\left(\text{Prefers}\right)\end{array}\right]\\ =\left(0.52\times 0.48\times 0.48\right)+\left(0.48\times 0.52\times 0.48\right)+\left(0.48\times 0.48\times 0.52\right)\\ =0.1198+0.1198+0.1198\\ =0.3594\end{array}$

Hence, the probability that exactly one of the three viewers prefers Leno is 0.3594.

To determine

Find the mean for Y.

Find the standard deviation for Y.

Answer to Problem 15E

The mean for Y is 1.57.

The standard deviation for Y is 0.8471.

Explanation of Solution

Calculation:

Mean:

For a discrete random variable Y and probability function $p\left(y\right)$, the expected value is,

$E\left(Y\right)={\displaystyle \sum _{y}yp\left(y\right)}$

The mean of random variable Y is,

$\begin{array}{c}E\left(Y\right)=0\left(0.1106\right)+1\left(0.3594\right)+2\left(0.3894\right)+3\left(0.1406\right)\\ =0+0.3594+0.7788+0.4218\\ =1.57\end{array}$

Hence, the mean for Y is 1.57.

Standard deviation:

For a discrete random variable Y with mean $E\left(Y\right)=\mu$, then the standard deviation is,

$\sigma =\sqrt{E\left[{\left(Y-\mu \right)}^2\right]}$

The standard deviation of random variable Y is,

$\begin{array}{c}\sigma =\sqrt{\left[0^2\left(0.1106\right)+1^2\left(0.3594\right)+2^2\left(0.3894\right)+3^2\left(0.1406\right)\right]-{\left(1.57\right)}^2}\\ =\sqrt{\left[0+0.3594+1.5576+1.2654\right]-2.4649}\\ =\sqrt{3.1824-2.4649}\\ =\sqrt{0.7175}\end{array}$

    $=0.8471$

Hence, the standard deviation for Y is 0.8471.

To determine

Find the probability that the number of viewers favoring Leno falls within 2 standard deviations of the mean.

Answer to Problem 15E

The probability that the number of viewers favoring Leno falls within 2 standard deviations of the mean is 1.

Explanation of Solution

Calculation:

Substitute 1.57 for $\mu$, and 0.8471 for $\sigma$ in the $\mu \pm 2\sigma$.

$\begin{array}{c}\mu \pm 2\sigma =1.57\pm 2\left(0.8471\right)\\ =1.57\pm 1.6942\\ =\left(1.57-1.6942,1.57+1.6942\right)\\ =\left(-0.124,3.264\right)\end{array}$

The limits are $-0.124<Y<3.264$, round the limits then $0<Y<3$, the probability that the value of Y falls in the interval $\mu \pm 2\sigma$ is,

$\begin{array}{c}P\left(0<Y<3\right)=P\left(Y=0\right)+P\left(Y=1\right)+P\left(Y=2\right)+P\left(Y=3\right)\\ =0.1106+0.3594+0.3894+0.1406\\ =1\end{array}$

Hence, the probability that the number of viewers favoring Leno falls within 2 standard deviations of the mean is 1.