Discrete Mathematics and Its Applications ( 8th International Edition ) ISBN:9781260091991
8th Edition
ISBN: 9781259731709
Author: ROSEN
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.2, Problem 23E
- Suppose that you have two different algorithms for solving a problem. To solve a problem of sizen, the first algorithm uses exactlyn(logn) operations and the second algorithm uses exactly
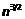operations. As n grows, which algorithm uses fewer operations?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
One bulb manufacturer claims an average bulb life of 1,600 hours. It is suspected that the actual average is significantly lower. To verify this, a sample of 49 bulbs is selected and the life of each bulb is measured. A sample mean of 1,500 hours and a standard deviation of 120 hours were obtained from them.
Can you be sure, at 5% significance, that the mean life is less than what the manufacturer claims?
The specification calls for the dimension of a certain mechanical part to be 0.55 inches. A random sample of 35 parts taken from a large batch showed a mean 0.54 in. with a deviation of 0.05 in.
Can it be concluded, at 1% significance, that the batch of parts meets the required specification?
Let
=
,
-2
X(t) = [ 6°
2t
e
-3e
-2t
X(t)=
2e-2t
-6e-
-2t
9].
Verify that the matrix ✗(t) is a fundamental matrix of the given linear system.
Determine a constant matrix C such that the given matrix Ŷ (t) can be represented as Ŷ(t) = X(t)C.
C =
help (matrices)
The determinant of the matrix C is help (numbers)
which is Choose . Therefore, the matrix ✗(t) is Choose
Book: Section 3.3 of Notes on Diffy Qs
Chapter 3 Solutions
Discrete Mathematics and Its Applications ( 8th International Edition ) ISBN:9781260091991
Ch. 3.1 - List all the steps used by Algorithm 1 to find the...Ch. 3.1 - Determine which characteristics of an algorithm...Ch. 3.1 - Devise an algorithm that finds the sum of all the...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Describe an algorithm that takes as input a list...Ch. 3.1 - Apalindromeis a string that reads the same forward...Ch. 3.1 - Devise an algorithm to computexn, wherexis a real...
Ch. 3.1 - Describe an algorithm that interchanges the values...Ch. 3.1 - cribe an algorithm that uses only assignment...Ch. 3.1 - List all the steps used to search for 9 in the...Ch. 3.1 - List all the steps used to search for 7 in the...Ch. 3.1 - cribe an algorithm that inserts an integerxin the...Ch. 3.1 - Describe an algorithm for finding the smallest...Ch. 3.1 - Describe an algorithm that locates the first...Ch. 3.1 - Describe an algorithm that locates the last...Ch. 3.1 - Describe an algorithm that produces the maximum,...Ch. 3.1 - Describe an algorithm for finding both the largest...Ch. 3.1 - Describe an algorithm that puts the first three...Ch. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Describe an algorithm that determines whether a...Ch. 3.1 - Describe an algorithm that will count the number...Ch. 3.1 - nge Algorithm 3 so that the binary search...Ch. 3.1 - Theternary search algorithmlocates an element in a...Ch. 3.1 - Specify the steps of an algorithm that locates an...Ch. 3.1 - Devise an algorithm that finds a mode in a list of...Ch. 3.1 - Devise an algorithm that finds all modes. (Recall...Ch. 3.1 - Two strings areanagramsif each can be formed from...Ch. 3.1 - ennreal numbersx1,x2,...,xn , find the two that...Ch. 3.1 - Devise an algorithm that finds the first term of a...Ch. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Use the bubble sort to sort 6, 2, 3, 1, 5, 4,...Ch. 3.1 - Use the bubble sort to sort 3, 1, 5, 7, 4, showing...Ch. 3.1 - Use the bubble sort to sortd,f,k,m,a,b, showing...Ch. 3.1 - Adapt the bubble sort algorithm so that it stops...Ch. 3.1 - Use the insertion sort to sort the list in...Ch. 3.1 - Use the insertion sort to sort the list in...Ch. 3.1 - Use the insertion sort to sort the list in...Ch. 3.1 - Sort these lists using the selection sort....Ch. 3.1 - Write the selection sort algorithm in pseudocode.Ch. 3.1 - Describe an algorithm based on the linear search...Ch. 3.1 - Describe an algorithm based on the binary search...Ch. 3.1 - How many comparisons does the insertion sort use...Ch. 3.1 - How many comparisons does the insertion sort use...Ch. 3.1 - Show all the steps used by the binary insertion...Ch. 3.1 - Compare the number of comparisons used by the...Ch. 3.1 - Prob. 51ECh. 3.1 - Devise a variation of the insertion sort that uses...Ch. 3.1 - Prob. 53ECh. 3.1 - List all the steps the naive string matcher uses...Ch. 3.1 - List all the steps the naive string matcher uses...Ch. 3.1 - Use the cashier’s algorithm to make change using...Ch. 3.1 - Use the cashier’s algorithm to make change using...Ch. 3.1 - Use the cashier’s algorithm to make change using...Ch. 3.1 - Prob. 59ECh. 3.1 - Show that if there were a coin worth 12 cents, the...Ch. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Devise a greedy algorithm that determines the...Ch. 3.1 - Suppose we have three menm1,m2, andm3and three...Ch. 3.1 - Write the deferred acceptance algorithm in...Ch. 3.1 - Prob. 66ECh. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prove that the Boyer-Moore majority vote algorithm...Ch. 3.1 - Show that the problem of determining whether a...Ch. 3.1 - Prob. 71ECh. 3.1 - Show that the problem of deciding whether a...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Prob. 11ECh. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - Exercises 1—14, to establish a big-Orelationship,...Ch. 3.2 - ermine whetherx3isO(g(x))for each of these...Ch. 3.2 - Explain what it means for a function to be 0(1)Ch. 3.2 - w that iff(x)isO(x)thenf(x)isO(x2).Ch. 3.2 - Suppose thatf(x),g(x), andh(x)are functions such...Ch. 3.2 - kbe a positive integer. Show...Ch. 3.2 - Prob. 19ECh. 3.2 - To simplify:(3a5)3 27a15 Given information:(3a5)3....Ch. 3.2 - ange the functionsn, 1000 logn,nlogn,2n!,2n,3n,...Ch. 3.2 - Arrange the...Ch. 3.2 - Suppose that you have two different algorithms for...Ch. 3.2 - Suppose that you have two different algorithms for...Ch. 3.2 - Give as good a big-Oestimate as possible for each...Ch. 3.2 - e a big-Oestimate for each of these functions. For...Ch. 3.2 - Give a big-Oestimate for each of these functions....Ch. 3.2 - each function in Exercise 1, determine whether...Ch. 3.2 - Prob. 29ECh. 3.2 - Show that each of these pairs of functions are of...Ch. 3.2 - Prob. 31ECh. 3.2 - w thatf(x)andg(x)are functions from the set of...Ch. 3.2 - Prob. 33ECh. 3.2 - Show that3x2+x+1is(3x2)by directly finding the...Ch. 3.2 - Prob. 35ECh. 3.2 - lain what it means for a function to be(1).Ch. 3.2 - Prob. 37ECh. 3.2 - Give a big-Oestimate of the product of the...Ch. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - pose thatf(x)isO(g(x)). Does it follow...Ch. 3.2 - Prob. 43ECh. 3.2 - pose thatf(x),g(x), andh(x)are functions such...Ch. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - ress the relationshipf(x)is(g(x))using a picture....Ch. 3.2 - Prob. 49ECh. 3.2 - w that iff(x)=anxn+an1xn1++a1x+a0,...Ch. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - w thatx5y3+x4y4+x3y5is(x3y3).Ch. 3.2 - w thatxyisO(xy).Ch. 3.2 - w thatxyis(xy).Ch. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.2 - (Requires calculus) Prove or disprove that (2n)!...Ch. 3.2 - Prob. 63ECh. 3.2 - Prob. 64ECh. 3.2 - Prob. 65ECh. 3.2 - Prob. 66ECh. 3.2 - Prob. 67ECh. 3.2 - Prob. 68ECh. 3.2 - Prob. 69ECh. 3.2 - Prob. 70ECh. 3.2 - Prob. 71ECh. 3.2 - Prob. 72ECh. 3.2 - Show thatnlognisO(logn!).Ch. 3.2 - Prob. 74ECh. 3.2 - Prob. 75ECh. 3.2 - Prob. 76ECh. 3.2 - (Requires calculus) For each of these pairs of...Ch. 3.3 - Give a big-Oestimate for the number of operations...Ch. 3.3 - Give a big-Oestimate for the number additions used...Ch. 3.3 - Give a big-Oestimate for the number of operations,...Ch. 3.3 - Give a big-Oestimate for the number of operations,...Ch. 3.3 - Prob. 5ECh. 3.3 - Use pseudocode to describe the algorithm that puts...Ch. 3.3 - Suppose that an element is known to be among the...Ch. 3.3 - Prob. 8ECh. 3.3 - Give a big-Oestimate for the number of comparisons...Ch. 3.3 - Show that this algorithm determines the number of...Ch. 3.3 - pose we havensubsetsS1,S2, ...,Snof the set {1, 2,...Ch. 3.3 - Consider the following algorithm, which takes as...Ch. 3.3 - The conventional algorithm for evaluating a...Ch. 3.3 - re is a more efficient algorithm (in terms of the...Ch. 3.3 - t is the largestnfor which one can solve within...Ch. 3.3 - What is the largestnfor which one can solve within...Ch. 3.3 - What is the largestnfor which one can solve within...Ch. 3.3 - How much time does an algorithm take to solve a...Ch. 3.3 - Prob. 19ECh. 3.3 - What is the effect in the time required to solve a...Ch. 3.3 - Prob. 21ECh. 3.3 - Determine the least number of comparisons, or...Ch. 3.3 - Analyze the average-case performance of the linear...Ch. 3.3 - An algorithm is calledoptimalfor the solution of a...Ch. 3.3 - Describe the worst-case time complexity, measured...Ch. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Analyze the worst-case time complexity of the...Ch. 3.3 - Analyze the worst-case time complexity of the...Ch. 3.3 - Analyze the worst-case time complexity of the...Ch. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Determine a big-O estimate for the worst-case...Ch. 3.3 - Determine the number of character comparisons used...Ch. 3.3 - Determine a big-Oestimate of the number of...Ch. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Show that the greedy algorithm for making change...Ch. 3.3 - rcises 41 and 42 deal with the problem of...Ch. 3.3 - rcises 41 and 42 deal with the problem of...Ch. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3 - Define the termalgorithm. What are the different...Ch. 3 - Describe, using English, an algorithm for finding...Ch. 3 - Prob. 3RQCh. 3 - Prob. 4RQCh. 3 - Prob. 5RQCh. 3 - Define what the worst-case time complexity,...Ch. 3 - Prob. 7RQCh. 3 - Describe the bubble sort algorithm. Use the bubble...Ch. 3 - Describe the insertion sort algorithm. Use the...Ch. 3 - Explain the concept of a greedy algorithm. Provide...Ch. 3 - Prob. 11RQCh. 3 - Describe an algorithm for locating the last...Ch. 3 - Prob. 2SECh. 3 - Give an algorithm to determine whether a bit...Ch. 3 - Suppose that a list contains integers that are in...Ch. 3 - Prob. 5SECh. 3 - Prob. 6SECh. 3 - Prob. 7SECh. 3 - Prob. 8SECh. 3 - Prob. 9SECh. 3 - Prob. 10SECh. 3 - Show the steps used by the shaker sort to sort the...Ch. 3 - Express the shaker sort in pseudocode.Ch. 3 - Prob. 13SECh. 3 - Prob. 14SECh. 3 - Prob. 15SECh. 3 - w that8x3+12x+100logxisO(x3).Ch. 3 - Prob. 17SECh. 3 - Prob. 18SECh. 3 - Prob. 19SECh. 3 - w thatnnis notO(n!).Ch. 3 - Prob. 21SECh. 3 - Prob. 22SECh. 3 - Prob. 23SECh. 3 - Prob. 24SECh. 3 - Arrange the...Ch. 3 - Prob. 26SECh. 3 - Prob. 27SECh. 3 - Show that if the denominations of coins arec0,c1,...Ch. 3 - Prob. 29SECh. 3 - Prob. 30SECh. 3 - Prob. 31SECh. 3 - Show that the deferred acceptance algorithm given...Ch. 3 - Prob. 33SECh. 3 - Show that when woman do the proposing in the...Ch. 3 - Prob. 35SECh. 3 - Prob. 36SECh. 3 - Prob. 37SECh. 3 - Prob. 38SECh. 3 - Prob. 39SECh. 3 - Prob. 40SECh. 3 - Prob. 41SECh. 3 - Exercises 4246 we will study the problem of load...Ch. 3 - Prob. 43SECh. 3 - Prob. 44SECh. 3 - Prob. 45SECh. 3 - Prove that the algorithm from Exercise 44 is a...Ch. 3 - Prob. 1CPCh. 3 - Prob. 2CPCh. 3 - Prob. 3CPCh. 3 - Prob. 4CPCh. 3 - Prob. 5CPCh. 3 - Prob. 6CPCh. 3 - Prob. 7CPCh. 3 - Given an integern, use the cashier’s algorithm to...Ch. 3 - Prob. 9CPCh. 3 - Prob. 10CPCh. 3 - Prob. 11CPCh. 3 - Prob. 1CAECh. 3 - Prob. 2CAECh. 3 - Using a generator of random orderings of the...Ch. 3 - Prob. 4CAECh. 3 - Write a program that animates the progress of all...Ch. 3 - Examine the history of the wordalgorithmand...Ch. 3 - Prob. 2WPCh. 3 - Explain how sorting algorithms can be classified...Ch. 3 - Prob. 4WPCh. 3 - Prob. 5WPCh. 3 - Prob. 6WPCh. 3 - Describe the historic trends in how quickly...Ch. 3 - Develop a detailed list of algorithmic paradigms...Ch. 3 - Explain what the Turing Award is and describe the...Ch. 3 - Prob. 10WPCh. 3 - Prob. 11WPCh. 3 - Describe six different NP-complete problems.Ch. 3 - Prob. 13WP
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- A manufacturer produces a wire rope of a certain type, which has a breaking strength of not more than 300 kg. A new and cheaper process is discovered which is desired to be employed, provided that the wire rope thus produced has an average breaking strength greater than 300 kg. If a random sample of 26 wires produced with the new process has given a mean of 304.5 kg and a standard deviation of 15 kg, should the manufacturer adopt the new process?arrow_forward5. mit answer urces Use Simpson's Rule and all the data in the following table to estimate the value of the 31 integral f(x) dx. 25 25 26 27 28 29 30 31 f(x) 4 44 4 -9 -2 9 2 5 (Round your answer to within two decimal places if necessary, but do not round until your final computation.) Simpson's Rule Approximation: PROGRES Score Completi 30 i Submit answer T The Weather Channel UP DELL FB F4 F5 F9 9. F10arrow_forwardFind the most general real-valued solution to the linear system of differential equations + C2 7-430 help (formulas) help (matrices) [*] »B] [8]: In the phase plane, this system is best described as a source/unstable node O sink / stable node saddle center point / ellipses spiral source spiral sink none of these Book: Section 3.5 of Notes on Diffy Qsarrow_forward
- Find the most general real-valued solution to the linear system of differential equations x x(t) y(t) = +C2 [*] [] [B] In the phase plane, this system is best described as a source/unstable node sink/stable node saddle center point / ellipses spiral source spiral sink none of these Book: Section 3.5 of Notes on Diffy Qs help (formulas) help (matrices)arrow_forwardFind the most general real-valued solution to the linear system of differential equations x(t) -9 8' [J - j (-8-8 y(t) In the phase plane, this system is best described as a source/unstable node sink/stable node saddle center point / ellipses spiral source spiral sink none of these Book: Section 3.5 of Notes on Diffy Qs -12 11 help (formulas) help (matrices)arrow_forwardFind the most general real-valued solution to the linear system of differential equations x(t) -2 7-730 --8-8 y(t) = In the phase plane, this system is best described as a source/unstable node sink / stable node saddle center point / ellipses spiral source spiral sink ☐ none of these Book: Section 3.5 of Notes on Diffy Qs 1 help (formulas) help (matrices)arrow_forward
- Consider the system of differential equations dx 8 3 x Y dt 4 -- (0) + (1) (음)- (0) dy 18 y. dt For this system, the eigenvalues are help (numbers) Enter as a comma separated list. How do the solution curves of the system above behave? All of the solutions curves would converge towards 0 (sink/stable node). All of the solution curves would run away from 0 (source/unstable node). The solution curves would race towards zero and then veer away towards infinity (saddle point). The solution curves converge to different points. The solution to the above differential equation with initial values x(0) = 5, y(0) = 3 is x(t) = help (formulas) y(t) = help (formulas) Book: Section 3.5 of Notes on Diffy Qsarrow_forwardConsider the system of differential equations Verify that x' x, x(0) = x(t) = c1e5t H + Cze³t [] is a solution to the system of differential equations for any choice of the constants C1 and C2. Find values of C1 and C2 that solve the given initial value problem. (According to the uniqueness theorem, you have found the unique solution of ' = Px, x(0) = 0). H e³t (t) = ( \ ) · e³ {}] + () ·³ [1] Book: Section 3.3 of Notes on Diffy Qs help (numbers)arrow_forwardFind the most general real-valued solution to the linear system of differential equations [5 -6 x = -10|| x(t) [*] [B] • [8] = C1 y(t) In the phase plane, this system is best described as a source/unstable node O sink / stable node saddle center point / ellipses spiral source spiral sink none of these Book: Section 3.5 of Notes on Diffy Qs help (formulas) help (matrices)arrow_forward
- Consider the system of higher order differential equations y″ = t¯¹y' + 7y – tz + (sint)z' + e5t, z" = y — 3z'. Rewrite the given system of two second order differential equations as a system of four first order linear differential equations of the form ÿ' = P(t)ÿ+ g(t). Use the following change of variables y' [Y] Y1 Y2 Y3 LY4_ help (formulas) help (matrices) Book: Section 3.3 of Notes on Diffy Qs [y1(t)] [ y(t)] Y2(t) y' (t) ÿ(t) = = Y3(t) z(t) Y₁(t)] [z'(t)]arrow_forwardCalculate the eigenvalues of this matrix: [21 12 A 24 -21 You'll probably want to use a calculator or computer to estimate the roots of the polynomial that defines the eigenvalues. The system has two real eigenvalues 1 and 2 where \1<\2 smaller eigenvalue \1 = help (numbers) associated eigenvector v1 larger eigenvalue 2 = = help (matrices) help (numbers) associated eigenvector v2 If x' = = B help (matrices) A is a differential equation, how do the solution curves behave? A. The solution curves diverge from different points on parallel paths. B. The solution curves would race towards zero and then veer away towards infinity. (saddle point) C. The solution curves converge to different points on parallel paths. D. All of the solution curves would run away from 0. (source / unstable node) E. All of the solutions curves would converge towards 0. (sink / stable node) Book: Section 3.5 of Notes on Diffy Qsarrow_forwardSuppose x = C1e2t [x(0)] Ly(0). Find C1 and C2. H == + C₂et [ - C1 = help (numbers) C₂ = help (numbers) 3 5 2 1 -3 -2 -1 2 3 -1 -2 -3 A 5 * x = Sketch the phase plane trajectory that satisfies the given initial condition. Which graph most closely resembles the graph you drew? Choose ✰ Is the solution curve headed toward or away from the origin as t increases? A. toward B. away C. neither toward nor away -3 N -1 3 2 1 -1 -2 -3 Book: Section 3.5 of Notes on Diffy Qs 0 3 5 2 1 -3 -2 -1 -1 -2 -3 - B 3 2 2 1 3 x * x * х 2 3 -3 -2 -1 2 3 -1 -2 -3 Darrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Implicit Differentiation with Transcendental Functions; Author: Mathispower4u;https://www.youtube.com/watch?v=16WoO59R88w;License: Standard YouTube License, CC-BY
How to determine the difference between an algebraic and transcendental expression; Author: Study Force;https://www.youtube.com/watch?v=xRht10w7ZOE;License: Standard YouTube License, CC-BY