College Algebra
10th Edition
ISBN: 9781337282291
Author: Ron Larson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.1, Problem 5E
In Exercises 5-8, match the quadratic function with its graph.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Find the perimeter and area
Assume {u1, U2, us} spans R³.
Select the best statement.
A. {U1, U2, us, u4} spans R³ unless u is the zero vector.
B. {U1, U2, us, u4} always spans R³.
C. {U1, U2, us, u4} spans R³ unless u is a scalar multiple of another vector in the set.
D. We do not have sufficient information to determine if {u₁, u2, 43, 114} spans R³.
OE. {U1, U2, 3, 4} never spans R³.
F. none of the above
Assume {u1, U2, 13, 14} spans R³.
Select the best statement.
A. {U1, U2, u3} never spans R³ since it is a proper subset of a spanning set.
B. {U1, U2, u3} spans R³ unless one of the vectors is the zero vector.
C. {u1, U2, us} spans R³ unless one of the vectors is a scalar multiple of another vector in the set.
D. {U1, U2, us} always spans R³.
E. {U1, U2, u3} may, but does not have to, span R³.
F. none of the above
Chapter 3 Solutions
College Algebra
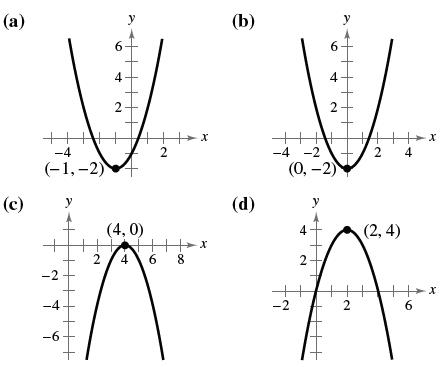
Ch. 3.1 - Sketch the graph of each quadratic function and...Ch. 3.1 - Prob. 2ECPCh. 3.1 - Sketch the graph of f(x)=x24x+3. Identify the...Ch. 3.1 - Write the standard form of the quadratic function...Ch. 3.1 - Rework Example 5 when the path of the baseball is...Ch. 3.1 - Prob. 1ECh. 3.1 - Fill in the blanks. A polynomial function of x...Ch. 3.1 - Fill in the blanks. A function is a second-degree...Ch. 3.1 - Fill in the blanks. When the graph of a quadratic...Ch. 3.1 - In Exercises 5-8, match the quadratic function...
Ch. 3.1 - In Exercises 5-8, match the quadratic function...Ch. 3.1 - In Exercises 5-8, match the quadratic function...Ch. 3.1 - In Exercises 5-8, match the quadratic function...Ch. 3.1 - Sketching Graphs of Quadratic Functions In...Ch. 3.1 - Sketching Graphs of Quadratic Functions In...Ch. 3.1 - Sketching Graphs of Quadratic Functions In...Ch. 3.1 - Sketching Graphs of Quadratic Functions In...Ch. 3.1 - In Exercises 13-26, write the quadratic function...Ch. 3.1 - In Exercises 13-26, write the quadratic function...Ch. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Prob. 19ECh. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Prob. 24ECh. 3.1 - Using Standard Form to Graph a Parabola In...Ch. 3.1 - Prob. 26ECh. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - In Exercises 27-34, use a graphing utility to...Ch. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - In Exercises 35 and 36, write the standard form of...Ch. 3.1 - In Exercises 35 and 36, write the standard form of...Ch. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Prob. 40ECh. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Prob. 42ECh. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Prob. 44ECh. 3.1 - Writing a Quadratic Function In Exercises 37-46,...Ch. 3.1 - Prob. 46ECh. 3.1 - In Exercises 47-50, determine the x-intercept(s)...Ch. 3.1 - Graphical Reasoning In Exercises 47-50, determine...Ch. 3.1 - Graphical Reasoning In Exercises 47-50, determine...Ch. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.1 - Prob. 52ECh. 3.1 - Prob. 53ECh. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - In Exercises 57-62, find two quadratic functions,...Ch. 3.1 - Prob. 62ECh. 3.1 - Prob. 63ECh. 3.1 - Prob. 64ECh. 3.1 - In Exercises 63-66, find two positive real numbers...Ch. 3.1 - In Exercises 63-66, find two positive real numbers...Ch. 3.1 - Path of a Diver The path of a diver is modeled by...Ch. 3.1 - Height of a Ball The path of a punted football is...Ch. 3.1 - Minimum Cost A manufacturer of lighting fixtures...Ch. 3.1 - Maximum Profit The profit P (in hundreds of...Ch. 3.1 - Maximum Revenue The total revenue R earned (in...Ch. 3.1 - Maximum Revenue The total revenue R earned per day...Ch. 3.1 - Maximum Area A rancher has 200 feet of fencing to...Ch. 3.1 - Maximum Area A Norman window is constructed by...Ch. 3.1 - Prob. 75ECh. 3.1 - Prob. 76ECh. 3.1 - Prob. 77ECh. 3.1 - Prob. 78ECh. 3.1 - Prob. 79ECh. 3.1 - The graph shows a quadratic function of the form...Ch. 3.1 - Proof Assume that the function f(x)=ax2+bx+c,a0...Ch. 3.2 - Sketch the graph of each function....Ch. 3.2 - Describe the left-hand and right-hand behavior of...Ch. 3.2 - Prob. 3ECPCh. 3.2 - Prob. 4ECPCh. 3.2 - Prob. 5ECPCh. 3.2 - Prob. 6ECPCh. 3.2 - Fill in the blanks. The graph of a polynomial...Ch. 3.2 - Fill in the blanks. The is used to determine...Ch. 3.2 - Fill in the blanks. A polynomial function of...Ch. 3.2 - Fill in the blanks. When x=a is a zero of a...Ch. 3.2 - Fill in the blanks. When a real zero xa of a...Ch. 3.2 - Fill in the blanks. A factor xak,k1, yields a ...Ch. 3.2 - Fill in the blanks. A polynomial function is...Ch. 3.2 - Fill in the blanks. The Theorem states that if fis...Ch. 3.2 - In Exercises 9-14, match the polynomial function...Ch. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - In Exercises 9-14, match the polynomial function...Ch. 3.2 - In Exercises 9-14, match the polynomial function...Ch. 3.2 - Sketching Transformations of Monomial Functions In...Ch. 3.2 - Prob. 16ECh. 3.2 - Sketching Transformations of Monomial Functions In...Ch. 3.2 - Prob. 18ECh. 3.2 - Applying the Leading Coefficient Test In Exercises...Ch. 3.2 - Applying the Leading Coefficient Test In Exercises...Ch. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - In Exercises 29-32, use a graphing utility to...Ch. 3.2 - In Exercises 29-32, use a graphing utility to...Ch. 3.2 - In Exercises 29-32, use a graphing utility to...Ch. 3.2 - In Exercises 29-32, use a graphing utility to...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - In Exercises 33-48, (a) find all real zeros of the...Ch. 3.2 - In Exercises 33-48, (a) find all real zeros of the...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Finding Real Zeros of a Polynomial Function In...Ch. 3.2 - Using Technology In Exercises 49-52, (a). use a...Ch. 3.2 - Using Technology In Exercises 49-52, (a). use a...Ch. 3.2 - Using Technology In Exercises 49-52, (a). use a...Ch. 3.2 - Using Technology In Exercises 49-52, (a). use a...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - In Exercises 53-62, find a polynomial function...Ch. 3.2 - Prob. 56ECh. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Prob. 58ECh. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 53-62,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Finding a Polynomial Function In Exercises 63-70,...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Prob. 72ECh. 3.2 - Prob. 73ECh. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Prob. 79ECh. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Prob. 81ECh. 3.2 - Prob. 82ECh. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Sketching the Graph of a Polynomial Function In...Ch. 3.2 - Using Technology In Exercises 85-88, use a...Ch. 3.2 - Prob. 86ECh. 3.2 - Prob. 87ECh. 3.2 - Prob. 88ECh. 3.2 - Prob. 89ECh. 3.2 - Using the Intermediate Value Theorem In Exercises...Ch. 3.2 - Prob. 91ECh. 3.2 - Prob. 92ECh. 3.2 - Maximum Volume You construct an open box from a...Ch. 3.2 - Maximum Volume You construct an open box with...Ch. 3.2 - Revenue The revenue R (in millions of dollars) for...Ch. 3.2 - Revenue The revenue R (in millions of dollars) for...Ch. 3.2 - Prob. 97ECh. 3.2 - Arboriculture The growth of a red oak tree is...Ch. 3.2 - True or False? In Exercises 99-102, determine...Ch. 3.2 - True or False? In Exercises 99-102, determine...Ch. 3.2 - True or False? In Exercises 99-102, determine...Ch. 3.2 - True or False? In Exercises 99-102, determine...Ch. 3.2 - Modeling Polynomials Sketch the graph of a...Ch. 3.2 - Modeling Polynomials Sketch the graph of a...Ch. 3.2 - Graphical Reasoning Sketch the graph of the...Ch. 3.2 - For each graph, describe a polynomial function...Ch. 3.2 - Prob. 107ECh. 3.3 - Divide the polynomial 9x3+36x249x196byx+4,and use...Ch. 3.3 - Divide x32x29byx3.Check the result.Ch. 3.3 - Prob. 3ECPCh. 3.3 - Prob. 4ECPCh. 3.3 - Prob. 5ECPCh. 3.3 - Prob. 6ECPCh. 3.3 - Two forms of the Division Algorithm are shown...Ch. 3.3 - In Exercises 2-6, fill in the blanks. In the...Ch. 3.3 - In Exercises 2-6, fill in the blanks. In the...Ch. 3.3 - In Exercises 2-6, fill in the blanks. A shortcut...Ch. 3.3 - In Exercises 2-6, fill in the blanks. The Theorem...Ch. 3.3 - In Exercises 2-6, fill in the blanks. The Theorem...Ch. 3.3 - Using the Division Algorithm In Exercises 7 and 8,...Ch. 3.3 - Using the Division Algorithm In Exercises 7 and 8,...Ch. 3.3 - Using Technology In Exercises 9 and 10, (a) use a...Ch. 3.3 - Prob. 10ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 14ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 16ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 18ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 20ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 22ECh. 3.3 - Long Division of Polynomials In Exercises 11-24,...Ch. 3.3 - Prob. 24ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 28ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 30ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 32ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 34ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 36ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 38ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 40ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 42ECh. 3.3 - Using Synthetic Division In Exercises 25-44, use...Ch. 3.3 - Prob. 44ECh. 3.3 - Using the Remainder Theorem In Exercises 45-50,...Ch. 3.3 - Using the Remainder Theorem In Exercises 45-50,...Ch. 3.3 - Using the Remainder Theorem In Exercises 45-50,...Ch. 3.3 - Prob. 48ECh. 3.3 - Using the Remainder Theorem In Exercises 45-50,...Ch. 3.3 - Prob. 50ECh. 3.3 - Using the Remainder Theorem In Exercises 51-54,...Ch. 3.3 - Prob. 52ECh. 3.3 - Using the Remainder Theorem In Exercises 51-54,...Ch. 3.3 - Prob. 54ECh. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Prob. 58ECh. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Prob. 60ECh. 3.3 - Using the Factor Theorem In Exercises 55-62, use...Ch. 3.3 - Prob. 62ECh. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Prob. 64ECh. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Prob. 68ECh. 3.3 - Factoring a Polynomial In Exercises 63-70, (a)...Ch. 3.3 - Prob. 70ECh. 3.3 - Approximating Zeros In Exercises 71-76, (a) use...Ch. 3.3 - Prob. 72ECh. 3.3 - Approximating Zeros In Exercises 71-76, (a) use...Ch. 3.3 - Prob. 74ECh. 3.3 - Prob. 75ECh. 3.3 - Prob. 76ECh. 3.3 - Prob. 77ECh. 3.3 - Prob. 78ECh. 3.3 - Prob. 79ECh. 3.3 - Prob. 80ECh. 3.3 - Profit A company that produces calculators...Ch. 3.3 - Lyme Disease The numbers Nof confirmed cases of...Ch. 3.3 - True or False? In Exercises 83-86, determine...Ch. 3.3 - True or False? In Exercises 83-86, determine...Ch. 3.3 - True or False? In Exercises 83-86, determine...Ch. 3.3 - Prob. 86ECh. 3.3 - Think About It In Exercises 87 and 88, perform the...Ch. 3.3 - Think About It In Exercises 87 and 88, perform the...Ch. 3.3 - Error Analysis Describe the error. Use synthetic...Ch. 3.3 - HOW DO YOU SEE IT? The graph below shows a...Ch. 3.3 - Exploration In Exercises 91 and 92, find the...Ch. 3.3 - Exploration In Exercises 91 and 92, find the...Ch. 3.3 - Think About It Find the value of k such that x4is...Ch. 3.4 - Determine the number of zeros of the polynomial...Ch. 3.4 - Prob. 2ECPCh. 3.4 - Prob. 3ECPCh. 3.4 - Find the rational zeros of fx=2x3+x213x+6.Ch. 3.4 - Find all real solutions of 2x35x2+15x+18=0.Ch. 3.4 - Find a fourth-degree polynomial function f with...Ch. 3.4 - Find the quartic (fourth-degree) polynomial...Ch. 3.4 - Prob. 8ECPCh. 3.4 - Prob. 9ECPCh. 3.4 - Prob. 10ECPCh. 3.4 - Find all real zeros of fx=8x34x2+6x3.Ch. 3.4 - Prob. 12ECPCh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Zeros of Polynomial Functions In Exercises 9-14,...Ch. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Zeros of Polynomial Functions In Exercises 9-14,...Ch. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Using the Rational Zero Test In Exercises 15-18,...Ch. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Using the Rational Zero Test In Exercises 19-28,...Ch. 3.4 - Using the Rational Zero Test In Exercises 19-28,...Ch. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Using the Rational Zero Test In Exercises 19-28,...Ch. 3.4 - Prob. 24ECh. 3.4 - Using the Rational Zero Test In Exercises 19-28,...Ch. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Prob. 28ECh. 3.4 - Prob. 29ECh. 3.4 - Solving a Polynomial Equation In Exercises 29-32,...Ch. 3.4 - Solving a Polynomial Equation In Exercises 29-32,...Ch. 3.4 - Prob. 32ECh. 3.4 - Using the Rational Zero Test In Exercises 33-36,...Ch. 3.4 - Using the Rational Zero Test In Exercises 33-36,...Ch. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Using the Rational Zero Test In Exercises 37-40,...Ch. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Prob. 42ECh. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Finding a Polynomial Function with Given Zeros In...Ch. 3.4 - Prob. 51ECh. 3.4 - Factoring a Polynomial In Exercises 51-54, write...Ch. 3.4 - Prob. 53ECh. 3.4 - Factoring a Polynomial In Exercises 51-54, write...Ch. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 57ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 59ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 61ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 63ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 65ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 67ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 69ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 73ECh. 3.4 - Finding the Zeros of a Polynomial Function In...Ch. 3.4 - Prob. 75ECh. 3.4 - Prob. 76ECh. 3.4 - Prob. 77ECh. 3.4 - Prob. 78ECh. 3.4 - Prob. 79ECh. 3.4 - Using Descartes’s Rule of Signs In Exercises...Ch. 3.4 - Prob. 81ECh. 3.4 - Using Descartes’s Rule of Signs In Exercises...Ch. 3.4 - Prob. 83ECh. 3.4 - Using Descartes’s Rule of Signs In Exercises...Ch. 3.4 - Prob. 85ECh. 3.4 - Prob. 86ECh. 3.4 - Prob. 87ECh. 3.4 - Prob. 88ECh. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Prob. 91ECh. 3.4 - Prob. 92ECh. 3.4 - Prob. 93ECh. 3.4 - Prob. 94ECh. 3.4 - Prob. 95ECh. 3.4 - Prob. 96ECh. 3.4 - Prob. 97ECh. 3.4 - Prob. 98ECh. 3.4 - Prob. 99ECh. 3.4 - Prob. 100ECh. 3.4 - Prob. 101ECh. 3.4 - Prob. 102ECh. 3.4 - Geometry You want to make an open box from a...Ch. 3.4 - Geometry A rectangular package to be sent by a...Ch. 3.4 - Prob. 105ECh. 3.4 - Prob. 106ECh. 3.4 - Prob. 107ECh. 3.4 - Prob. 108ECh. 3.4 - Prob. 109ECh. 3.4 - Prob. 110ECh. 3.4 - Prob. 111ECh. 3.4 - Prob. 112ECh. 3.4 - Prob. 113ECh. 3.4 - Prob. 114ECh. 3.4 - Prob. 115ECh. 3.4 - Think About It Sketch the graph of a fifth-degree...Ch. 3.4 - Writing an Equation In Exercises 117 and 118, the...Ch. 3.4 - Prob. 118ECh. 3.4 - Prob. 119ECh. 3.4 - Prob. 120ECh. 3.4 - Prob. 121ECh. 3.4 - Prob. 122ECh. 3.4 - Prob. 123ECh. 3.5 - The ordered pairs below give the median sales...Ch. 3.5 - Prob. 2ECPCh. 3.5 - The simple interest on an investment is directly...Ch. 3.5 - Neglecting air resistance, the distance s an...Ch. 3.5 - Prob. 5ECPCh. 3.5 - The resistance of a copper wire carrying an...Ch. 3.5 - The kinetic energy E of an object varies jointly...Ch. 3.5 - Fill in the blanks. Two techniques for fitting...Ch. 3.5 - Fill in the blanks. Statisticians use a measure...Ch. 3.5 - Fill in the blanks. The linear model with the...Ch. 3.5 - Fill in the blanks. An r-value, or, of a set of...Ch. 3.5 - Fill in the blanks. The direct variation model...Ch. 3.5 - Fill in the blanks. The mathematical model y=2xis...Ch. 3.5 - Fill in the blanks. Mathematical models that...Ch. 3.5 - Fill in the blanks. The joint variation model...Ch. 3.5 - Mathematical Models In Exercises 9 and 10, (a)...Ch. 3.5 - Mathematical Models In Exercises 9 and 10, (a)...Ch. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Prob. 12ECh. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Sketching a Line In Exercises 11-16, sketch the...Ch. 3.5 - Sports The ordered pairs below give the winning...Ch. 3.5 - Broadway The ordered pairs below give the starting...Ch. 3.5 - Direct Variation In Exercises 19-24, find a direct...Ch. 3.5 - Prob. 20ECh. 3.5 - Direct Variation In Exercises 19-24, find a direct...Ch. 3.5 - Prob. 22ECh. 3.5 - Direct Variation In Exercises 19-24, find a direct...Ch. 3.5 - Direct Variation In Exercises 19-24, find a direct...Ch. 3.5 - Direct Variation as an nthPower In Exercises...Ch. 3.5 - Prob. 26ECh. 3.5 - Direct Variation as an nthPower In Exercises...Ch. 3.5 - Direct Variation as an nthPower In Exercises...Ch. 3.5 - Inverse Variation as an nth Power In Exercises...Ch. 3.5 - Prob. 30ECh. 3.5 - Inverse Variation as an nth Power In Exercises...Ch. 3.5 - Prob. 32ECh. 3.5 - Think About It In Exercises 33 and 34, use the...Ch. 3.5 - Think About It In Exercises 33 and 34, use the...Ch. 3.5 - Determining Variation In Exercises 35-38,...Ch. 3.5 - Prob. 36ECh. 3.5 - Determining Variation In Exercises 35-38,...Ch. 3.5 - Determining Variation In Exercises 35-38,...Ch. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Prob. 40ECh. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Prob. 42ECh. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Prob. 44ECh. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Prob. 46ECh. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Finding a Mathematical Model In Exercises 39-48,...Ch. 3.5 - Describing a Formula In Exercises 49-52, use...Ch. 3.5 - Prob. 50ECh. 3.5 - Describing a Formula In Exercises 49-52, use...Ch. 3.5 - Describing a Formula In Exercises 49-52, use...Ch. 3.5 - Finding a Mathematical Model In Exercises 53-60,...Ch. 3.5 - Prob. 54ECh. 3.5 - Finding a Mathematical Model In Exercises 53-60,...Ch. 3.5 - Prob. 56ECh. 3.5 - Finding a Mathematical Model In Exercises 53-60,...Ch. 3.5 - Prob. 58ECh. 3.5 - Finding a Mathematical Model In Exercises 53-60,...Ch. 3.5 - Prob. 60ECh. 3.5 - Simple Interest The simple interest on an...Ch. 3.5 - Prob. 62ECh. 3.5 - Measurement Use the fact that 13 inches is...Ch. 3.5 - Measurement Use the fact that 14 gallons is...Ch. 3.5 - Hooke’s Law In Exercises 65-68, use Hooke’s Law,...Ch. 3.5 - Hooke’s Law In Exercises 65-68, use Hooke’s Law,...Ch. 3.5 - Hooke’s Law In Exercises 65-68, use Hooke’s Law,...Ch. 3.5 - Hooke’s Law In Exercises 65-68, use Hooke’s Law,...Ch. 3.5 - Ecology The diameter of the largest particle that...Ch. 3.5 - Work The work W required to lift an object varies...Ch. 3.5 - Prob. 71ECh. 3.5 - Prob. 72ECh. 3.5 - Music The fundamental frequency (in hertz) of a...Ch. 3.5 - Beam Load The maximum load that a horizontal beam...Ch. 3.5 - Prob. 75ECh. 3.5 - Prob. 76ECh. 3.5 - Prob. 77ECh. 3.5 - HOW DO YOU SEE IT? Discuss how well a linear model...Ch. 3.5 - Prob. 79ECh. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Using Standard Form to Graph a Parabola In...Ch. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Geometry The perimeter of a rectangle is...Ch. 3 - Maximum Revenue The total revenue R earned (in...Ch. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Maximum Revenue A small theater has a seating...Ch. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Finding Real Zeros of a Polynomial Function In...Ch. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Using the Intermediate Value Theorem In Exercises...Ch. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Using the Intermediate Value Theorem In Exercises...Ch. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Using Synthetic Division In Exercises 57-60, use...Ch. 3 - Using Synthetic Division In Exercises 57-60, use...Ch. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Prob. 69RECh. 3 - Prob. 70RECh. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Using the Rational Zero Test In Exercises 75-80,...Ch. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Prob. 78RECh. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Prob. 81RECh. 3 - Prob. 82RECh. 3 - Prob. 83RECh. 3 - Prob. 84RECh. 3 - Prob. 85RECh. 3 - Prob. 86RECh. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - Prob. 89RECh. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - Using Descartes’s Rule of Signs In Exercises 93...Ch. 3 - Prob. 94RECh. 3 - Prob. 95RECh. 3 - Prob. 96RECh. 3 - Prob. 97RECh. 3 - Prob. 98RECh. 3 - Prob. 99RECh. 3 - Prob. 100RECh. 3 - Measurement A billboard says that it is 12.5 miles...Ch. 3 - Energy The power P produced by a wind turbine is...Ch. 3 - Frictional Force The frictional force F between...Ch. 3 - Demand A company has found that the daily demand x...Ch. 3 - Prob. 105RECh. 3 - Cost The cost of constructing a wooden box with a...Ch. 3 - Prob. 107RECh. 3 - Prob. 108RECh. 3 - Prob. 109RECh. 3 - Prob. 110RECh. 3 - Writing Explain the connections between factors of...Ch. 3 - Prob. 1TCh. 3 - Prob. 2TCh. 3 - Write the standard form of the equation of the...Ch. 3 - The path of a ball is modeled by the function...Ch. 3 - Prob. 5TCh. 3 - Prob. 6TCh. 3 - Divide using synthetic division. 2x43x2+4x1x+2Ch. 3 - Use synthetic division to show that x=3 is a zero...Ch. 3 - In Exercises 9 and 10, find the rational zeros of...Ch. 3 - Prob. 10TCh. 3 - In Exercises 11 and 12, find a polynomial function...Ch. 3 - Prob. 12TCh. 3 - In Exercises 13 and 14, find all the zeros of the...Ch. 3 - In Exercises 13 and 14, find all the zeros of the...Ch. 3 - In Exercises 15-17, find a mathematical model that...Ch. 3 - In Exercises 15-17, find a mathematical model that...Ch. 3 - In Exercises 15-17, find a mathematical model that...Ch. 3 - Prob. 18TCh. 3 - Prob. 1PSCh. 3 - Prob. 2PSCh. 3 - Building a Quonset Hut Quonset huts were developed...Ch. 3 - Prob. 4PSCh. 3 - Prob. 5PSCh. 3 - Prob. 6PSCh. 3 - Sums and Products of Zeros (a) Complete the table....Ch. 3 - Prob. 8PSCh. 3 - Finding the Equation of a Parabola The parabola...Ch. 3 - Prob. 10PSCh. 3 - Prob. 11PSCh. 3 - Prob. 12PSCh. 3 - Finding Dimensions At a glassware factory, molten...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Let H = span {u, v}. For each of the following sets of vectors determine whether H is a line or a plane. Select an Answer u = 3 1. -10 8-8 -2 ,v= 5 Select an Answer -2 u = 3 4 2. + 9 ,v= 6arrow_forwardSolve for the matrix X: X (2 7³) x + ( 2 ) - (112) 6 14 8arrow_forward5. Solve for the matrix X. (Hint: we can solve AX -1 = B whenever A is invertible) 2 3 0 Χ 2 = 3 1arrow_forward
- Write p(x) = 6+11x+6x² as a linear combination of ƒ (x) = 2+x+4x² and g(x) = 1−x+3x² and h(x)=3+2x+5x²arrow_forward3. Let M = (a) - (b) 2 −1 1 -1 2 7 4 -22 Find a basis for Col(M). Find a basis for Null(M).arrow_forwardSchoology X 1. IXL-Write a system of X Project Check #5 | Schx Thomas Edison essay, x Untitled presentation ixl.com/math/algebra-1/write-a-system-of-equations-given-a-graph d.net bookmarks Play Gimkit! - Enter... Imported Imported (1) Thomas Edison Inv... ◄›) What system of equations does the graph show? -8 -6 -4 -2 y 8 LO 6 4 2 -2 -4 -6 -8. 2 4 6 8 Write the equations in slope-intercept form. Simplify any fractions. y = y = = 00 S olo 20arrow_forward
- EXERCICE 2: 6.5 points Le plan complexe est rapporté à un repère orthonormé (O, u, v ).Soit [0,[. 1/a. Résoudre dans l'équation (E₁): z2-2z+2 = 0. Ecrire les solutions sous forme exponentielle. I b. En déduire les solutions de l'équation (E2): z6-2 z³ + 2 = 0. 1-2 2/ Résoudre dans C l'équation (E): z² - 2z+1+e2i0 = 0. Ecrire les solutions sous forme exponentielle. 3/ On considère les points A, B et C d'affixes respectives: ZA = 1 + ie 10, zB = 1-ie 10 et zc = 2. a. Déterminer l'ensemble EA décrit par le point A lorsque e varie sur [0, 1. b. Calculer l'affixe du milieu K du segment [AB]. C. Déduire l'ensemble EB décrit par le point B lorsque varie sur [0,¹ [. d. Montrer que OACB est un parallelogramme. e. Donner une mesure de l'angle orienté (OA, OB) puis déterminer pour que OACB soit un carré.arrow_forward2 Use grouping to factor: 10x + 13x + 3 = 0 Identify A B and C in the chart below feach responce inarrow_forward2 Use grouping to factor: 10x² + 13x + 3 = 0 Identify A, B, and C in the chart below. (each rearrow_forward
- 2 Use grouping to factor: 10x + 13x + 3 = 0 Identify A B and C in the chart below feach responce inarrow_forwardUse grouping to fully factor: x³ + 3x² - 16x - 48 = 0 3 2arrow_forwardName: Tay Jones Level Two Date: Algebra 3 Unit 3: Functions and Equations Practice Assessment Class: #7-OneNote 1. The function f(x) = x² is transformed in the following functions. List the vertex for each function, circle whether the function opens up or down, and why. All three parts must be correct to receive Level 2 points. You can receive points for a, b, and c. a) g(x) = -2(x+5)² Vertex: Opens Up Opens Down Why? ais negative -2 Vertex: b) g(x) = (x + 2)² - 3 c) g(x) = -4(x + 2)² + 2 Opens Up Opens Down Vertex: Opens Up Opens Down Why? 4 Ca is negative) Why? his positive 2. The graph of the function f(x) is shown below. Find the domain, range, and end behavior. Then list the values of x for which the function values are increasing and decreasing. f(x) Domain: End Behavior: As x → ∞o, f(x) -> -6 As x, f(x) -> Range: Where is it Increasing? (002] Where is it Decreasing? (1,00)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
What is a Relation? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=hV1_wvsdJCE;License: Standard YouTube License, CC-BY
RELATIONS-DOMAIN, RANGE AND CO-DOMAIN (RELATIONS AND FUNCTIONS CBSE/ ISC MATHS); Author: Neha Agrawal Mathematically Inclined;https://www.youtube.com/watch?v=u4IQh46VoU4;License: Standard YouTube License, CC-BY