Chapter 3.1, Problem 17E

The expansion of a 3 × 3 determinant can be remembered by the following device. Write a second copy of the first two columns to the tight of the matrix, and compute the determinant by multiplying entries on six diagonals:

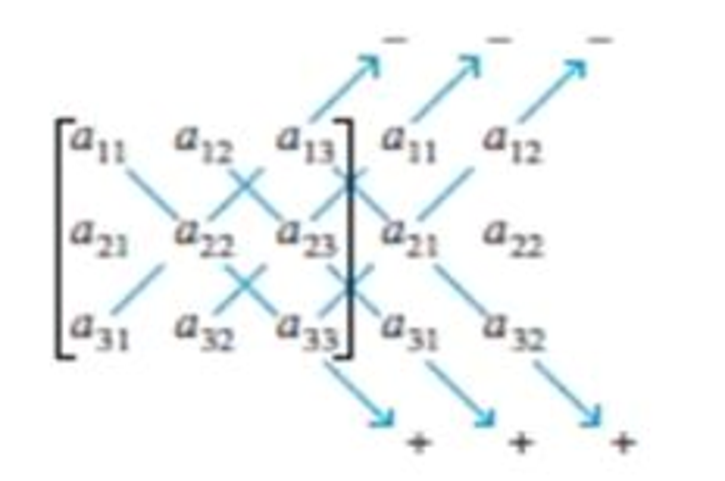
Add the downward diagonal products and subtract the up-ward products. Use this method to compute the determinants in Exercises 15–18. Warning: This trick does not generalize in any reasonable way to 4 × 4 or larger matrices.

17. $\left|\begin{array}{ccc}2& -3& 3\\ 3& 2& 2\\ 1& 3& -1\end{array}\right|$