Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.1, Problem 12E
In Exercises 9 to 12, congruent parts are indicated by like dashes (sides) or arcs (angles). State which method (SSS, SAS. ASA, or AAS) would be used to prove the two
 |
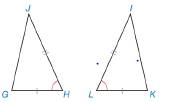Expert Solution & Answer
Trending nowThis is a popular solution!
Chapter 3 Solutions
Elementary Geometry for College Students
Ch. 3.1 - In Exercises 1 to 4, consider the congruent...Ch. 3.1 - In Exercises 1 to 4. consider the congruent...Ch. 3.1 - In Exercises 1 to 4. consider the congruent...Ch. 3.1 - In Exercises 1 to 4, consider the congruent...Ch. 3.1 - Consider ABC and ABD in the figure shown. By the...Ch. 3.1 - In a right triangle, the sides that form the right...Ch. 3.1 - In ABC, the midpoints of the sides are joined. a...Ch. 3.1 - a. Suppose that you wish to prove that RSTSRV....Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 9 to 12, congruent parts are...
Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 19 and 20, the triangles to be proved...Ch. 3.1 - In Exercises 19 and 20, the triangles to be proved...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 25 and 26, complete each proof. Use...Ch. 3.1 - In Exercises 25 and 26, complete each proof. Use...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 33 to 36, the methods to be used are...Ch. 3.1 - In Exercises 33 to 36, the methods to be used are...Ch. 3.1 - In Exercises 33 to 36, the method to be used are...Ch. 3.1 - In Exercises 33 to 36, the method to be used are...Ch. 3.1 - In quadrilateral ABCD, AC and BD are perpendicular...Ch. 3.1 - In ABC and DEF, you know that AD, CF, and ABDE....Ch. 3.1 - Prob. 39ECh. 3.1 - In Exercises 39 to 40, complete each proof. Given:...Ch. 3.1 - Given: ABC; RS is the perpendicular bisector of...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - Prob. 9ECh. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Given: HJ bisects KHL HJKL See figure for exercise...Ch. 3.2 - Given: HJ bisects KHL HJKL In Exercise 15, you cam...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - In Exercises 30 to 32, draw the triangles that are...Ch. 3.2 - Given: RW bisects SRU Prove: RSRU TRUVRS HINT:...Ch. 3.2 - Given: DBBC and CEDE Prove: ABAE BDCECD HINT:...Ch. 3.2 - In the roof truss shown, AB=8 and mHAF=37. Find: a...Ch. 3.2 - In the support system of the bridge shown, AC=6ft...Ch. 3.2 - As a car moves along the roadway in a mountain...Ch. 3.2 - Because of the construction along the road from A...Ch. 3.2 - Given: Regular pentagon ABCDE with diagonals BE...Ch. 3.2 - In the figure with regular pentagon ABCDE, do BE...Ch. 3.3 - For Exercises 1 to 8, use the accompanying...Ch. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - For Exercises 1 to 8, use the accompanying...Ch. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - In Exercises 9 to 12, determine whether the sets...Ch. 3.3 - Prob. 10ECh. 3.3 - In Exercises 9 to 12, determine whether the sets...Ch. 3.3 - In Exercises 9 to 12, determine whether the sets...Ch. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - Prob. 14ECh. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Is it possible for a triangle to be: a an acute...Ch. 3.3 - Prob. 21ECh. 3.3 - In concave quadrilateral ABCD, the angle at A...Ch. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Suppose that ABCDEF. Also, AX bisects CAB and DY...Ch. 3.3 - Suppose that ABCDEF. Also, AX is the median from A...Ch. 3.3 - In Exercises 35 and 36, complete each proof using...Ch. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - In isosceles triangle BAT, ABAT.Also, BRBTAR, if...Ch. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Given: In the figure, XZYZ and Z is the midpoint...Ch. 3.3 - Prob. 48ECh. 3.4 - In Exercises 1 to 6, use line segments of given...Ch. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - In Exercises 13 and 14. use the angles and lengths...Ch. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - In Exercises 23 to 26, use line segments of length...Ch. 3.4 - Prob. 24ECh. 3.4 - In Exercises 23 to 26, use line segments of length...Ch. 3.4 - Prob. 26ECh. 3.4 - In Exercise 27 and 28, use the given angle R and...Ch. 3.4 - Prob. 28ECh. 3.4 - Complete the justification of the construction of...Ch. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Draw a right triangle and construct the angle...Ch. 3.4 - Draw an obtuse triangle and construct the three...Ch. 3.4 - Prob. 38ECh. 3.4 - A carpenter has placed a square over an angle in...Ch. 3.4 - Prob. 40ECh. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - Is it possible to draw a triangle whose angles...Ch. 3.5 - Is it possible to draw a triangle whose angles...Ch. 3.5 - Is it possible to draw a triangle whose sides...Ch. 3.5 - Is it possible to draw a triangle whose sides...Ch. 3.5 - Prob. 15ECh. 3.5 - In Exercises 15 to 18, describe the triangle XYZ ,...Ch. 3.5 - Prob. 17ECh. 3.5 - In Exercises 15 to 18, describe the triangle XYZ ,...Ch. 3.5 - Two of the sides of an isosceles triangle have...Ch. 3.5 - The sides of a right triangle have lengths of 6cm,...Ch. 3.5 - Prob. 21ECh. 3.5 - One of the angles of an isosceles triangle...Ch. 3.5 - Prob. 23ECh. 3.5 - A tornado has just struck a small Kansas community...Ch. 3.5 - In Exercises 25 and 26, complete each proof shown...Ch. 3.5 - Prob. 26ECh. 3.5 - In Exercises 27 and 28, construct proofs. Given:...Ch. 3.5 - In Exercises 27 and 28, construct proofs. Given:...Ch. 3.5 - Prob. 29ECh. 3.5 - In MNP not shown, point Q lies on NP so that MQ...Ch. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - Prob. 33ECh. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - Prove by the indirect method: Given: MPN is not...Ch. 3.5 - Prove by the indirect method: Given: Scalene XYZ...Ch. 3.5 - In Exercises 37 and 38, prove each theorem. The...Ch. 3.5 - In Exercises 37 and 38, prove each theorem. The...Ch. 3.CR - Given: AEBDEC AEDE Prove: AEBDECCh. 3.CR - Given: ABEFACDF12 Prove: BECh. 3.CR - Given: AD bisects BC ABBCDCBC Prove: AEDECh. 3.CR - Prob. 4CRCh. 3.CR - Prob. 5CRCh. 3.CR - Given: B is the midpoint of AC BDAC Prove: ADC is...Ch. 3.CR - Prob. 7CRCh. 3.CR - Prob. 8CRCh. 3.CR - Given: YZ is the base of an isosceles triangle;...Ch. 3.CR - Prob. 10CRCh. 3.CR - Prob. 11CRCh. 3.CR - Prob. 12CRCh. 3.CR - Prob. 13CRCh. 3.CR - Given: AC bisects BAD Prove: ADCDCh. 3.CR - Prob. 15CRCh. 3.CR - Prob. 16CRCh. 3.CR - Prob. 17CRCh. 3.CR - Name the longest line segment shown in...Ch. 3.CR - Prob. 19CRCh. 3.CR - Two sides of a triangle have lengths 15 and 20....Ch. 3.CR - Prob. 21CRCh. 3.CR - Prob. 22CRCh. 3.CR - Prob. 23CRCh. 3.CR - Prob. 24CRCh. 3.CR - Given: ABC is isosceles with base AB...Ch. 3.CR - Prob. 26CRCh. 3.CR - Prob. 27CRCh. 3.CR - Construct a right triangle that has acute angle A...Ch. 3.CR - Construct a second isosceles triangle in which the...Ch. 3.CT - It is given that ABCDEF triangles not shown a If...Ch. 3.CT - Consider XYZ triangles not shown a Which side is...Ch. 3.CT - Prob. 3CTCh. 3.CT - Prob. 4CTCh. 3.CT - With congruent parts marked, are the two triangles...Ch. 3.CT - Prob. 6CTCh. 3.CT - Prob. 7CTCh. 3.CT - CM is the median for ABC from vertex C to side AB....Ch. 3.CT - Prob. 9CTCh. 3.CT - Prob. 10CTCh. 3.CT - Prob. 11CTCh. 3.CT - Show all arcs in the following construction....Ch. 3.CT - Prob. 13CTCh. 3.CT - Prob. 14CTCh. 3.CT - Prob. 15CTCh. 3.CT - Prob. 16CTCh. 3.CT - Complete all statements and reasons for the...Ch. 3.CT - Complete all missing statements and reasons in the...Ch. 3.CT - The perimeter of an isosceles triangle is 32cm. If...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Is it possible to draw a triangle whose sides measure a. 8, 9, and 10? b. 8, 9, and 17? c. 8, 9, and 18?arrow_forwardThe bisectors of two consecutive angles of HJKL are shown. What can you conclude regarding P?arrow_forwardIs it possible to draw a triangle whose angles measure a. 100, 100, and 60? b. 45, 45, and 90?arrow_forward
- RSTV is a kite, with RSST and RVVT. If mSTV=40, how large is the angle formed a by the bisectors of RST and STV? b by the bisectors of SRV and RST?arrow_forwardA carpenter joins four boards of lengths 6 ft, 6 ft, 4 ft, and 4 ft, in that order, to form quadrilateral ABCD as shown. a What type of quadrilateral is formed? b How are angles B and D related?arrow_forwardIn square ABCD not shown, point E lies on side DC. If AB=8 and AE=10, find BE.arrow_forward
- In concave quadrilateral ABCD, the angle at A measures 40. ABD is isosceles, BC bisects ABD, and DC bisects ADB. What are the measures of ABC, ADC, and 1?arrow_forwardWhat is the acronym that is used to represent each statement? a Corresponding angles of similar triangles are congruent. b Corresponding sides of similar triangles are proportional.arrow_forwardDraw a triangle and, by construction, find its incenter.arrow_forward
- a Is it really necessary to construct all three bisectors of the angles of a triangle to locate its incenter? b Is it really necessary to construct all three perpendicular bisectors of the sides of a triangle to locate its circumcenter?arrow_forwardIn ABC,mCAB=80,mACB=60,andABC=40. With the angle bisectors as shown, which line segment is longer? a AE or EC? b CD or DB? c AF or FB?arrow_forwardConsider any triangle and one exterior angle at each vertex. What is the sum of the measures of the measures of the three exterior angle of the triangles?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License