
Concept explainers
Cosmic rays are high-energy charged particles produced by astronomical objects. Many of the cosmic rays that make their way to the Earth are trapped by the Earth’s magnetic field and never reach the surface. These trapped cosmic rays are found in the Van Allen belts—donut-shaped zones over the Earth’s equator (Fig. 30.34). These cosmic rays are mostly protons with energies of about 30 MeV. The inset in the figure shows a cosmic ray proton as it is about to enter the Earth’s magnetic field. The cosmic ray’s velocity is initially perpendicular to the field. Three students discuss what happens to the incoming cosmic ray. Decide which student or students are correct.
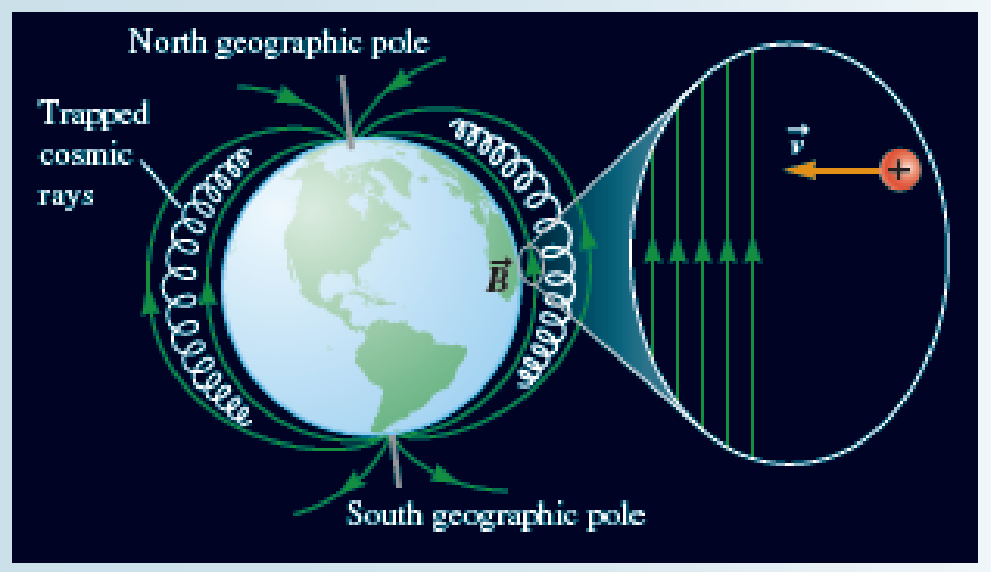
Figure 30.34 The Van Allen belts are donut-shaped zones of trapped cosmic rays above the Earth’s surface. Inset: What happens to this cosmic ray as it enters the Earth’s magnetic field?
Shannon: The velocity is perpendicular to the magnetic field, so the cosmic ray just passes through the field and hits the Earth’s atmosphere.
Avi: What you are saying is that the magnetic field exerts no force on the cosmic ray. Actually, it exerts a huge force because the velocity is perpendicular to the magnetic field. The force will be into the page.
Cameron: Avi is right. The cosmic ray proton is going to feel a huge magnetic force. Because it is positively charged, it will be pushed upward along the magnetic field lines.
Shannon: I never said the force was zero. There is a force, but the force is perpendicular to the magnetic field lines. In this case, that’s to the left—toward the Earth.
Avi: The force is perpendicular to the magnetic field, but it also has to be perpendicular to the velocity. Because
Want to see the full answer?
Check out a sample textbook solution
Chapter 30 Solutions
Physics For Scientists And Engineers: Foundations And Connections, Extended Version With Modern Physics
- An extremely long, solid nonconducting cylinder has a radius Ro. The charge density within the cylinder is a function of the distance R from the axis, given by PE (R) = po(R/Ro)², po > 0.arrow_forwardA sky diver of mass 90 kg (with suit and gear) is falling at terminal speed. What is the upward force of air drag, and how do you know?arrow_forwardA car is traveling at top speed on the Bonneville salt flats while attempting a land speed record. The tires exert 25 kN of force in the backward direction on the ground. Why backwards? How large are the forces resisting the forward motion of the car, and why?arrow_forward
- Please help by: Use a free body diagram Show the equations State your assumptions Show your steps Box your final answer Thanks!arrow_forwardPlease help by: Use a free body diagram Show the equations State your assumptions Show your steps Box your final answer Thanks!arrow_forwardBy please don't use Chatgpt will upvote and give handwritten solutionarrow_forward
- A collection of electric charges that share a common magnitude q (lower case) has been placed at the corners of a square, and an additional charge with magnitude Q (upper case) is located at the center of that square. The signs of the charges are indicated explicitly such that ∣∣+q∣∣∣∣+Q∣∣=∣∣−q∣∣==∣∣−Q∣∣=qQ Four unique setups of charges are displayed. By moving one of the direction drawings from near the bottom to the bucket beside each of the setups, indicate the direction of the net electric force on the charge with magnitude Q, located near the center, else indicate that the magnitude of the net electric force is zero, if appropriate.arrow_forwardA number of electric charges has been placed at distinct points along a line with separations as indicated. Two charges share a common magnitude, q (lower case), and another charge has magnitude Q(upper case). The signs of the charges are indicated explicitly such that ∣∣+q∣∣∣∣+Q∣∣=∣∣−q∣∣==∣∣−Q∣∣=qQ Four different configurations of charges are shown. For each, express the net electric force on the charge with magnitude Q (upper case) as F⃗E=FE,xî where the positive x direction is towards the right. By repositioning the figures to the area on the right, rank the configurations from the most negative value to the most positive value of FE,x.arrow_forwardFor each part make sure to include sign to represent direction, with up being positive and down being negative. A ball is thrown vertically upward with a speed of 30.5 m/s. A) How high does it rise? y= B) How long does it take to reach its highest point? t= C) How long does it take the ball return to its starting point after it reaches its highest point? t= D) What is its velocity when it returns to the level from which it started? v=arrow_forward

 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning





