1 Introduction: The Nature Of Science And Physics 2 Kinematics 3 Two-dimensional Kinematics 4 Dynamics: Force And Newton's Laws Of Motion 5 Further Applications Of Newton's Laws: Friction, Drag, And Elasticity 6 Uniform Circular Motion And Gravitation 7 Work, Energy, And Energy Resources 8 Linear Momentum And Collisions 9 Statics And Torque 10 Rotational Motion And Angular Momentum 11 Fluid Statics 12 Fluid Dynamics And Its Biological And Medical Applications 13 Temperature, Kinetic Theory, And The Gas Laws 14 Heat And Heat Transfer Methods 15 Thermodynamics 16 Oscillatory Motion And Waves 17 Physics Of Hearing 18 Electric Charge And Electric Field 19 Electric Potential And Electric Field 20 Electric Current, Resistance, And Ohm's Law 21 Circuits And Dc Instruments 22 Magnetism 23 Electromagnetic Induction, Ac Circuits, And Electrical Technologies 24 Electromagnetic Waves 25 Geometric Optics 26 Vision And Optical Instruments 27 Wave Optics 28 Special Relativity 29 Introduction To Quantum Physics 30 Atomic Physics 31 Radioactivity And Nuclear Physics 32 Medical Applications Of Nuclear Physics 33 Particle Physics 34 Frontiers Of Physics expand_more
Chapter Questions expand_more
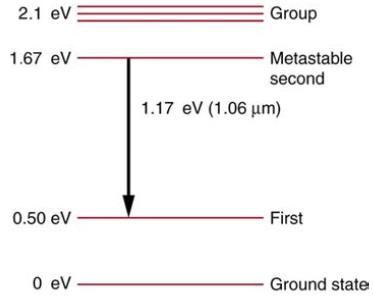
Problem 1CQ: Name three different types of evidence for the existence of atoms. Problem 2CQ: Explain why patterns observed in the periodic table of the elements are evidence for the existence... Problem 3CQ: If atoms exist, why can't we see them with visible light? Problem 4CQ: What two pieces of evidence allowed the first calculation of me, the mass of the electron? (a) The... Problem 5CQ: How do the allowed orbits for electrons in atoms differ from the allowed orbits for planets around... Problem 6CQ: How do the allowed orbits for electrons in atoms differ from the allowed orbits for planets around... Problem 7CQ: Explain how Bohr's rule for the quantization of electron orbital angular momentum differs from the... Problem 8CQ: What is a hydrogen-like atom, and how are the energies and radii of its electron orbits related to... Problem 9CQ: Explain why characteristic x rays are the most energetic in the EM emission spectrum of a given... Problem 10CQ: Why does the energy of characteristic x rays become increasingly greater for heavier atoms? Problem 11CQ: Observers at a safe distance from atmospheric test of a nuclear bomb feel its heat but receive none... Problem 12CQ: Lasers are used to burn and read CDs. Explain why a laser that emits blue light would be capable of... Problem 13CQ: Crystal lattices can be examined with x rays but not UV. Why? Problem 14CQ: CT scanners do not detect details smaller than about 0.5 Is this limitation clue to the wavelength... Problem 15CQ: How do the allowed orbits for electrons in atoms differ from the allowed orbits for planets around... Problem 16CQ: Atomic and molecular spectra are discrete. What does discrete mean, and how are discrete spectra... Problem 17CQ: Hydrogen gas can only absorb EM radiation that has an energy corresponding to a transition in the... Problem 18CQ: Lasers are used to burn and read CDs. Explain why a laser that emits blue light would be capable of... Problem 19CQ: The coating on the inside of fluorescent light tubes absorbs ultraviolet light and subsequently... Problem 20CQ: What is the difference between fluorescence and phosphorescence? Problem 21CQ: How can you tell that a hologram is a true three-dimensional image and that those in 3-D movies are... Problem 22CQ: How is the de Broglie wavelength of electrons related to the quantization of their orbits in atoms... Problem 23CQ: What is the Zeeman effect, and what type of quantization was discovered because of this effect? Problem 24CQ: Define the quantum numbers n,l,ml,s, and ms. Problem 25CQ: For a given value of n, what are the allowed values of l? Problem 26CQ: For a given value of l, what are the allowed values of ml ? What are the allowed values of ml for a... Problem 27CQ: List all the possible values of s and msfor an electron. Are there particles for which these values... Problem 28CQ: Identify the shell, subshell, and number of electrons for the following: (a) 2P3. (b)4d9. (c) 3s1.... Problem 29CQ: Which of the following are not allowed? State which rule is violated for any that are not allowed.... Problem 1PE: Using the given charge-to-mass ratios for electrons and protons, and knowing the magnitudes of their... Problem 2PE: (a) Calculate the mass of a proton using the charge-to-mass ratio given for it in this chapter and... Problem 3PE: If someone wanted to build a scale model of the atom with a nucleus 1.00 m in diameter, how far away... Problem 4PE: Rutherford found the size of the nucleus to be about 10-15 m. This implied a huge density. What... Problem 5PE: In Millikan's oil-drop experiment, one looks at a small oil drop held motionless between two plates.... Problem 6PE: (a) An aspiring physicist wants to build a scale model of a hydrogen atom for her science fair... Problem 7PE: By calculating its wavelength, show that the first line in the Lyman series is UV radiation. Problem 8PE: Find the wavelength of the third line in the Lyman series, and identify the type of EM radiation. Problem 9PE: Look up the values of the quantities in aB=h242mekqe2, and verify that the Bohr radius aB is... Problem 10PE: Verify that the ground state energy E0 is 13.6 eV by using E0=22qe4mek2h2. Problem 11PE: If a hydrogen atom has its electron in the n=4 state, how much energy in eV is needed to ionize it? Problem 12PE: A hydrogen atom in an excited state can be ionized with less energy than when it is in its ground... Problem 13PE: Find the radius of a hydrogen atom in the n=2 state according to Bohr's theory. Problem 14PE: Show that (13.6eV)/hc=1.097107m=R (Rydberg's constant), as discussed in the text. Problem 15PE: What is the smallest-wavelength line in the Balmer series? Is it in the visible part of the... Problem 16PE: Show that the entire Paschen series is in the infrared part of the spectrum. To do this, you only... Problem 17PE: Do the Balmer and Lyman series overlap? To answer this, calculate the shortest-wavelength Balmer... Problem 18PE: (a) Which line in the Balmer series is the first one in the UV part of the spectrum? (b) How many... Problem 19PE: A wavelength of 4.653 m is observed in a hydrogen spectrum for a transition that ends in the nf=5... Problem 20PE: A singly ionized helium ion has only one electron and is denoted He+. What is the ion's radius in... Problem 21PE: A beryllium ion with a single electron (denoted Be3+) is in an excited state with radius the same as... Problem 22PE: Atoms can be ionized by thermal collisions, such as at the high temperatures found in the solar... Problem 23PE: Verify Equations rn=n2ZaB and aB=h242mekqe2=0.5291010 m using the approach stated in the text. That... Problem 24PE: The wavelength of the four Balmer series lines for hydrogen are found to be 410.3, 434.2, 486.3, and... Problem 25PE: (a) What is the shortest-wavelength x-ray radiation that can be generated in an x-ray tube with an... Problem 26PE: A color television tube also generates some x rays when its electron beam strikes the screen. What... Problem 27PE: An x ray tube has an applied voltage of 100 kV. (a) What is the most energetic x-ray photon it can... Problem 28PE: The maximum characteristic x-ray photon energy comes from the capture of a free electron into a K... Problem 29PE: What are the approximate energies of the K and K rays for copper? Problem 30PE: Figure 30.39 shows the energy-level diagram for neon. (a) Verity that the energy of the photon... Problem 31PE: A helium-neon laser is pumped by electric discharge. What wavelength electromagnetic radiation would... Problem 32PE: Ruby lasers have chromium atoms doped in an aluminum oxide crystal. The energy level diagram for... Problem 33PE: (a) What energy photons can pump chromium atoms in a ruby laser from the ground state to its second... Problem 34PE: Some of the most powerful lasers are based on the energy levels of neodymium in solids, such as... Problem 35PE: If an atom has an electron in the n=5 state with m1=3, what are the possible values of l ? Problem 36PE: An atom has an electron with m1=2. What is the smallest value of n for this electron? Problem 37PE: What are the possible values of m1 for an electron in the n=4 state? Problem 38PE: What, if any, constraints does a value of ml=1 place on the other quantum numbers for an electron in... Problem 39PE: (a) Calculate the magnitude of the angular momentum for an l=1 electron. (b) Compare your answer to... Problem 40PE: (a) What is the magnitude of the angular momentum for an l=1 electron? (b) Calculate the magnitude... Problem 41PE: Repeat Exercise 30.40 for l=3. Problem 42PE: (a) How many angles can L make with the z-axis for an l=2 electron? (b) Calculate the value of the... Problem 43PE: What angles can the spin S of an electron make with the Z-axis? Problem 44PE: (a) How many electrons can be in the n=4 shell? (b) What are its subshells, and how many electrons... Problem 45PE: (a) What is the minimum value of 1 for a subshell that has 11 electrons in it? (b) If this subshell... Problem 46PE: (a) If one subshell of an atom has 9 electrons in it, what is the minimum value of l ? (b) What is... Problem 47PE: (a) List all possible sets of quantum numbers (n,l,ml,ms) for the n=3 shell, and determine the... Problem 48PE: Which of the following spectroscopic notations are not allowed? (a) 5s1(b) 1d1(c) 4s3(d) 3p7(e)... Problem 49PE: Which of the following spectroscopic notations are allowed (that is, which violate none of the rules... Problem 50PE: (a) Using the Pauli exclusion principle and the rules relating the allowed values of the quantum... Problem 51PE: Integrated Concepts Estimate the density of a nucleus by calculating the density of a proton, taking... Problem 52PE: Integrated Concepts The electric and magnetic forces on an electron in the CRT in Figure 30.7 are... Problem 53PE: (a) What is the distance between the slits of a diffraction grating that produces a first-order... Problem 54PE: Integrated Concepts A galaxy moving away from the earth has a speed of 0.0100c. What wavelength do... Problem 55PE: Integrated Concepts Calculate the velocity of a star moving relative to the earth if you observe a... Problem 56PE: Integrated Concepts In a Millikan oil-drop experiment using a setup like that in Figure 30.9, a... Problem 57PE: Integrated Concepts What double-slit separation would produce a first-order maximum at 3.00° for... Problem 58PE: Integrated Concepts In a laboratory experiment designed to duplicate Thomson's determination of... Problem 59PE: Integrated Concepts Find the value of l, the orbital angular momentum quantum number, for the moon... Problem 60PE: Integrated Concepts Particles called muons exist in cosmic rays and can be created in particle... Problem 61PE: Integrated Concepts Calculate the minimum amount of energy in joules needed to create a population... Problem 62PE: Integrated Concepts A carbon dioxide laser used in surgery emits infrared radiation with a... Problem 63PE: Integrated Concepts Suppose an MRI scanner uses 100-MHz radio waves. (a) Calculate the photon... Problem 64PE: Integrated Concepts (a) An excimer laser used for vision correction emits 193-nm UV. Calculate the... Problem 65PE: Integrated Concepts A neighboring galaxy rotates on its axis so that stars on one side move toward... Problem 66PE: Integrated Concepts A pulsar is a rapidly spinning remnant of a supernova. It rotates on its axis,... Problem 67PE: Integrated Concepts Prove that the velocity of charged particles moving along a straight path... Problem 68PE: Unreasonable Results (a) What voltage must be applied to an X-ray tube to obtain... Problem 69PE: Unreasonable Results A student in a physics laboratory observes a hydrogen spectrum with a... Problem 70PE: Construct Your Own Problem The solar corona is so hot that most atoms in it are ionized. Consider a... Problem 71PE: Construct Your Own Problem Consider the Doppler-shifted hydrogen spectrum received from a rapidly... format_list_bulleted


 University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning




