Chapter 30, Problem 14A

To determine

(h)

Measurement of the length for dimension (h).

Answer to Problem 14A

Measurement of the length is ${\frac{9}{16}}^{\prime \text{}\prime }$.

Explanation of Solution

Given:

The line is given below:

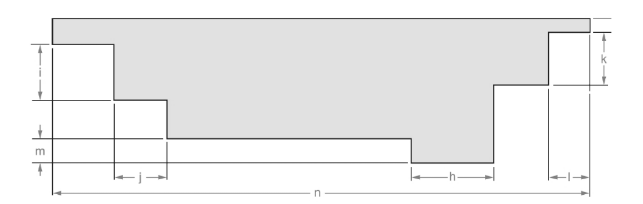
Concept used:

Length is measured with the help of inch scale.

Calculation:

Attached the inch scale over given length.

From the above figure, the length of the line can be measured as follows:

  $\begin{array}{l}L=18{\left(\frac{1}{32}\right)}^{\prime \text{}\prime }\\ L={\frac{9}{16}}^{\prime \text{}\prime }\end{array}$

Thus, measurement of the length is ${\frac{9}{16}}^{\prime \text{}\prime }$.

Conclusion:

Measurement of the length is ${\frac{9}{16}}^{\prime \text{}\prime }$.

To determine

(i)

Measurement of the length for dimension (i).

Answer to Problem 14A

Measurement of the length is ${\frac{3}{16}}^{\prime \text{}\prime }$.

Explanation of Solution

Given:

The line is given below:

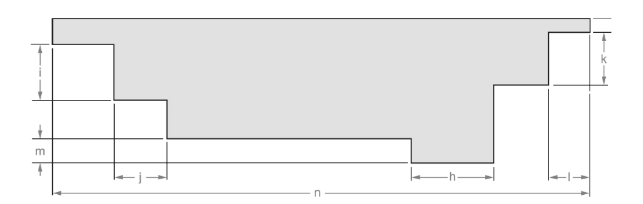
Concept used:

Length is measured with the help of inch scale.

Calculation:

Attached the inch scale over given length.

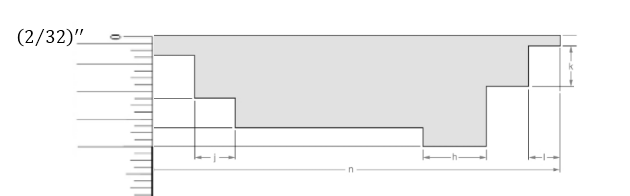
From the above figure, the length of the line can be measured as follows:

  $\begin{array}{l}L=6{\left(\frac{1}{32}\right)}^{\prime \text{}\prime }\\ L={\frac{3}{16}}^{\prime \text{}\prime }\end{array}$

Thus, measurement of the length is ${\frac{3}{16}}^{\prime \text{}\prime }$.

Conclusion:

Measurement of the length is ${\frac{3}{16}}^{\prime \text{}\prime }$.

To determine

(j)

Measurement of the length for dimension (j).

Answer to Problem 14A

Measurement of the length is ${\frac{3}{8}}^{\prime \text{}\prime }$.

Explanation of Solution

Given:

The line is given below:

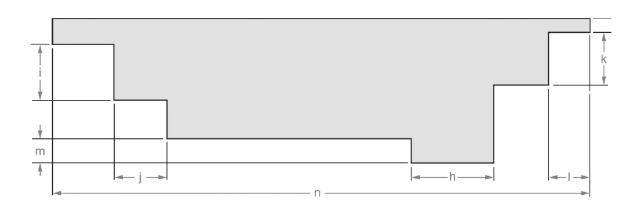
Concept used:

Length is measured with the help of inch scale.

Calculation:

Attached the inch scale over given length.

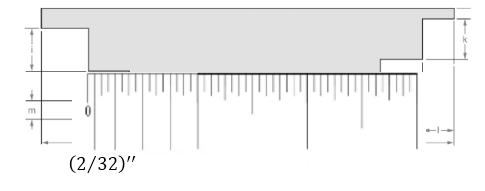
From the above figure, the length of the line can be measured as follows:

  $\begin{array}{l}L=12{\left(\frac{1}{32}\right)}^{\prime \text{}\prime }\\ L={\frac{3}{8}}^{\prime \text{}\prime }\end{array}$

Thus, measurement of the length is ${\frac{3}{8}}^{\prime \text{}\prime }$.

Conclusion:

Measurement of the length is ${\frac{3}{8}}^{\prime \text{}\prime }$.

To determine

(k)

Measurement of the length for dimension (k).

Answer to Problem 14A

Measurement of the length is ${\frac{11}{32}}^{\prime \text{}\prime }$.

Explanation of Solution

Given:

The line is given below:

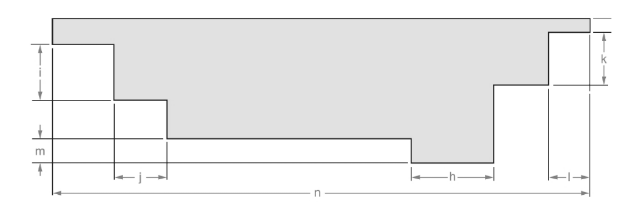
Concept used:

Length is measured with the help of inch scale.

Calculation:

Attached the inch scale over given length.

From the above figure, the length of the line can be measured as follows:

  $\begin{array}{l}L=11{\left(\frac{1}{32}\right)}^{\prime \text{}\prime }\\ L={\frac{11}{32}}^{\prime \text{}\prime }\end{array}$

Thus, measurement of the length is ${\frac{11}{32}}^{\prime \text{}\prime }$.

Conclusion:

Measurement of the length is ${\frac{11}{32}}^{\prime \text{}\prime }$.

To determine

(l)

Measurement of the length for dimension (l).

Answer to Problem 14A

Measurement of the length is ${\frac{9}{32}}^{\prime \text{}\prime }$.

Explanation of Solution

Given:

The line is given below:

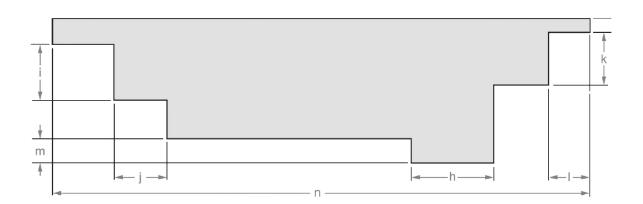
Concept used:

Length is measured with the help of inch scale.

Calculation:

Attached the inch scale over given length.

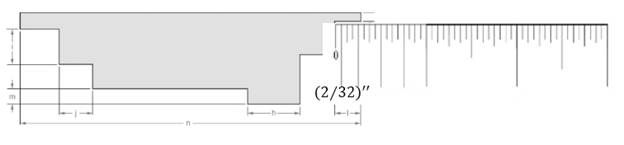
From the above figure, the length of the line can be measured as follows:

  $\begin{array}{l}L=9{\left(\frac{1}{32}\right)}^{\prime \text{}\prime }\\ L={\frac{9}{32}}^{\prime \text{}\prime }\end{array}$

Thus, measurement of the length is ${\frac{9}{32}}^{\prime \text{}\prime }$.

Conclusion:

Measurement of the length is ${\frac{9}{32}}^{\prime \text{}\prime }$.

To determine

(m)

Measurement of the length for dimension (m).

Answer to Problem 14A

Measurement of the length is ${\frac{3}{16}}^{\prime \text{}\prime }$.

Explanation of Solution

Given:

The line is given below:

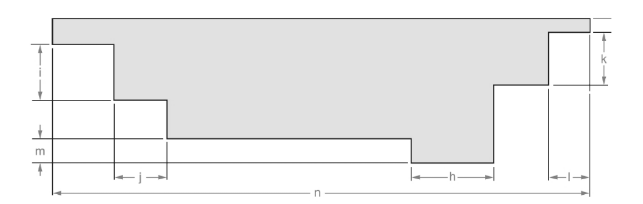
Concept used:

Length is measured with the help of inch scale.

Calculation:

Attached the inch scale over given length.

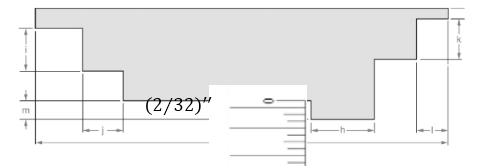
From the above figure, the length of the line can be measured as follows:

  $\begin{array}{l}L=6{\left(\frac{1}{32}\right)}^{\prime \text{}\prime }\\ L={\frac{3}{16}}^{\prime \text{}\prime }\end{array}$

Thus, measurement of the length is ${\frac{3}{16}}^{\prime \text{}\prime }$.

Conclusion:

Measurement of the length is ${\frac{3}{16}}^{\prime \text{}\prime }$.

To determine

(n)

Measurement of the length for dimension (n).

Answer to Problem 14A

Measurement of the length is $3{\frac{15}{32}}^{\prime \text{}\prime }$.

Explanation of Solution

Given:

The line is given below:

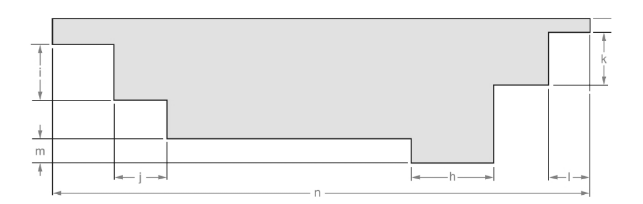
Concept used:

Length is measured with the help of inch scale.

Calculation:

Attached the inch scale over given length.

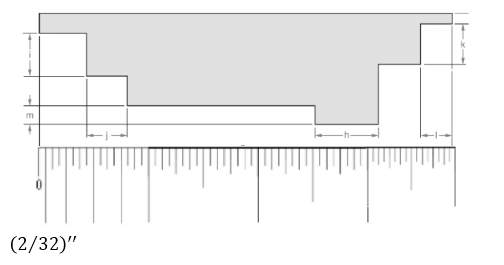
From the above figure, the length of the line can be measured as follows:

  $\begin{array}{l}L=3^{″}+15{\left(\frac{1}{32}\right)}^{\prime \text{}\prime }\\ L=3{\frac{15}{32}}^{\prime \text{}\prime }\end{array}$

Thus, measurement of the length is $3{\frac{15}{32}}^{\prime \text{}\prime }$.

Conclusion:

Measurement of the length is $3{\frac{15}{32}}^{\prime \text{}\prime }$.