Calculus & Its Applications
Calculus & Its Applications
12th Edition
ISBN: 9780137590810
Author: Larry J. Goldstein, David C. Lay, David I. Schneider, Nakhle H. Asmar, William Edward Tavernetti
Publisher: PEARSON
bartleby

Videos

Textbook Question
Book Icon
Chapter 3, Problem 38RE

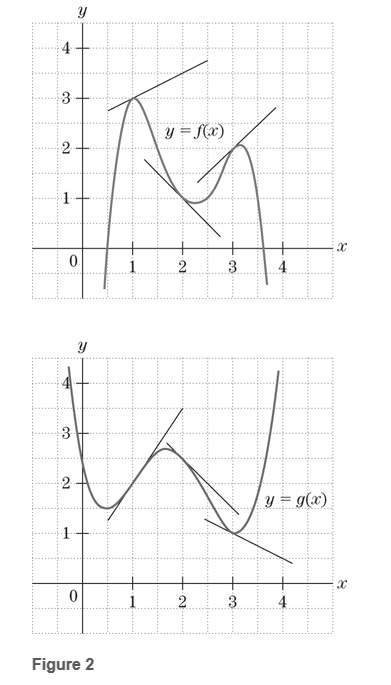
Exercises 33 – 38 refer to the graphs of the functions f ( x ) and g ( x ) in Fig. 2. Determine h ( 1 ) and h ' ( 1 ) .

Chapter 3, Problem 38RE, Exercises 33 38 refer to the graphs of the functions f(x) and g(x) in Fig. 2. Determine h(1) and

h ( x ) = g ( f ( x ) )

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 3, Problem 37RE
Next
Chapter 3, Problem 39RE
Students have asked these similar questions
Does the series converge or diverge
Does the series converge or diverge
Diverge or conver

Chapter 3 Solutions

Calculus & Its Applications

Ch. 3.1 - Consider the function y=(x+1)x. Differentiate y by...Ch. 3.1 - Prob. 2CYUCh. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28. y=xxCh. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28. y=[...
Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Prob. 18ECh. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28. y=[...Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Find the equation of the tangent line to the curve...Ch. 3.1 - Find the equation of the tangent line to the curve...Ch. 3.1 - Find all x-coordinates of points (x,y) on the...Ch. 3.1 - Find the inflection points on the graph of...Ch. 3.1 - Find all x such that dydx=0, where...Ch. 3.1 - The graph of y=(x21)4(x2+1)5 is shown in Fig. 3....Ch. 3.1 - Find the point(s) on the graph of y=(x2+3x1)/x...Ch. 3.1 - Find the point(s) on the graph of y=(2x4+1)(x5)...Ch. 3.1 - Find d2ydx2. y=(x2+1)4Ch. 3.1 - Find d2ydx2. y=x2+1Ch. 3.1 - Find d2ydx2 y=xx+1Ch. 3.1 - Find d2ydx2 y=22+x2Ch. 3.1 - In Exercises 4144, a function h(x) is defined in...Ch. 3.1 - In Exercises 4144, a function h(x) is defined in...Ch. 3.1 - In Exercises 4144, a function h(x) is defined in...Ch. 3.1 - In Exercises 4144, a function h(x) is defined in...Ch. 3.1 - Volume An open rectangular box is 3 feet long and...Ch. 3.1 - Volume A closed rectangular box is to be...Ch. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Average Revenue Let R(x) be the revenue received...Ch. 3.1 - Average Velocity Let s(t) be the number of miles a...Ch. 3.1 - Prob. 51ECh. 3.1 - Cost-Benefit of Emission Control A manufacturer...Ch. 3.1 - In Exercises 53 and 54, use the fact that at the...Ch. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - Prob. 57ECh. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - If f(x) and g(x) are differentiable functions such...Ch. 3.1 - If f(x) and g(x) are differentiable functions such...Ch. 3.1 - Prob. 62ECh. 3.1 - Let f(x)=1/x and g(x)=x3. Show that the product...Ch. 3.1 - Prob. 64ECh. 3.1 - Prob. 65ECh. 3.1 - Prob. 66ECh. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prob. 69ECh. 3.2 - Consider the function h(x)=(2x35)5+(2x35)4 Write...Ch. 3.2 - Consider the function h(x)=(2x35)5+(2x35)4 Compute...Ch. 3.2 - Prob. 3CYUCh. 3.2 - Compute f(g(x)), where f(x) and g(x) are the...Ch. 3.2 - Compute f(g(x)), where f(x) and g(x) are the...Ch. 3.2 - Compute f(g(x)), where f(x) and g(x) are the...Ch. 3.2 - Compute f(g(x)), where f(x) and g(x) are the...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - In Exercises 2126, a function h(x) is defined in...Ch. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - In Exercises 2126, a function h(x) is defined in...Ch. 3.2 - In Exercises 2126, a function h(x) is defined in...Ch. 3.2 - Prob. 26ECh. 3.2 - Sketch the graph of y=4x/(x+1)2,x1.Ch. 3.2 - Sketch the graph of y=2/(1+x2)Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute dydx using the chain rule in formula (1)....Ch. 3.2 - Compute dydx using the chain rule in formula (1)....Ch. 3.2 - Compute dydx using the chain rule in formula (1)....Ch. 3.2 - Prob. 40ECh. 3.2 - Compute dydxt=t0 y=x23x,x=t2+3,t0=0Ch. 3.2 - Compute dydxt=t0 y=(x22x+4)2,x=1t+1,t0=1Ch. 3.2 - Compute dydxt=t0 y=x+1x1,x=t24,t0=3Ch. 3.2 - Prob. 44ECh. 3.2 - Find the equation of the line tangent to the graph...Ch. 3.2 - Find the equation of the line tangent to the graph...Ch. 3.2 - Find the x- coordinate of all points on the curve...Ch. 3.2 - The function f(x)=x26x+10 has one relative minimum...Ch. 3.2 - Prob. 49ECh. 3.2 - Allometric Equation Many relations in biology are...Ch. 3.2 - Suppose that P, y and t are variables, where P is...Ch. 3.2 - Suppose that Q, x and y are variables, where Q is...Ch. 3.2 - Marginal Profit and Times Rate of Change When a...Ch. 3.2 - Marginal Cost and Time Rate of Change The cost of...Ch. 3.2 - A model for Carbon Monoxide Levels Ecologists...Ch. 3.2 - Profit A manufacturer of microcomputers estimates...Ch. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - If f(x) and g(x) are differentiable functions,...Ch. 3.2 - Prob. 60ECh. 3.2 - Effect of Stocks on Total Assets of a Company...Ch. 3.2 - Refer to Exercise 61. Use chain rule to find...Ch. 3.2 - Refer to Exercise 61. Find dxdt|t=2.5 and...Ch. 3.2 - Refer to Exercise 61. What was the maximum value...Ch. 3.2 - In an expression of the form f(g(x)), f(x) is...Ch. 3.3 - Solution can be found following the section...Ch. 3.3 - Solution can be found following the section...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Find the equation of the tangent line to the graph...Ch. 3.3 - Find the equation of the tangent line to the graph...Ch. 3.3 - Slope of the Lemniscate The graph of...Ch. 3.3 - The graph of x4+2x2y2+y4=9x29y2 is a lemniscate...Ch. 3.3 - Marginal Rate of Substitution Suppose that x and y...Ch. 3.3 - Demand Equation Suppose that x and y represents...Ch. 3.3 - In Exercise 31 36, suppose that x and y are both...Ch. 3.3 - In Exercise 31 36, suppose that x and y are both...Ch. 3.3 - In Exercise 31 36, suppose that x and y are both...Ch. 3.3 - Prob. 34ECh. 3.3 - In Exercise 31 36, suppose that x and y are both...Ch. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Demand Equation Suppose that the price p (in...Ch. 3.3 - Demand Equation Suppose that the price p (in...Ch. 3.3 - Advertising Affects Revenue The monthly...Ch. 3.3 - Rate of Change of Price Suppose that in Boston the...Ch. 3.3 - Related Rates Figure 7 shows a 10- foot ladder...Ch. 3.3 - Related Rates An airplane flying 390 feet per...Ch. 3.3 - Related Rates A baseball diamond is a 90- foot by...Ch. 3.3 - Related Rates A motorcyclist is driving over a...Ch. 3 - State the product rule and quotient rule.Ch. 3 - Prob. 2FCCECh. 3 - Prob. 3FCCECh. 3 - Prob. 4FCCECh. 3 - Prob. 5FCCECh. 3 - Prob. 6FCCECh. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions. y=x(x51)3Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions. y=xx+4Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions. y=x26xx2Ch. 3 - Differentiate the following functions. y=2x23xCh. 3 - Differentiate the following functions. y=(3x2x3)2Ch. 3 - Differentiate the following functions. y=x3+xx2xCh. 3 - Let f(x)=(3x+1)4(3x)5. Find all x such that...Ch. 3 - Let f(x)=x2+1x2+5. Find all x such that f(x)=0.Ch. 3 - Find the equation of the line tangent to the graph...Ch. 3 - Find the equation of the line tangent to the graph...Ch. 3 - Minimizing Area A botanical display is to be...Ch. 3 - Repeat Exercise 17, with the sidewalk on the...Ch. 3 - Cost function A store estimates that its cost when...Ch. 3 - Rate of Change of Taxes A company pays y dollars...Ch. 3 - In Exercise 21-23, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 21-23, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 21-23, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 24-26, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 24-26, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 24-26, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 27-29, find dydx, where y is a...Ch. 3 - In Exercise 27-29, find dydx, where y is a...Ch. 3 - In Exercise 27-29, find dydx, where y is a...Ch. 3 - In Exercises 30 32, find dydx, where y is a...Ch. 3 - In Exercises 30 32, find dydx, where y is a...Ch. 3 - In Exercises 30 32, find dydx, where y is a...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Revenue Function The revenue, R, that a company...Ch. 3 - Amount of Drug Usage The amount, A, of anesthetics...Ch. 3 - The graph of x2/3+y2/3=8 is the astroid in Fig. 3...Ch. 3 - Slope of the Folium of Descartes The graph of...Ch. 3 - Slope of the Folium of Descartes The graph of...Ch. 3 - In Exercises 43-46, x and y are related by the...Ch. 3 - In Exercises 43-46, x and y are related by the...Ch. 3 - In Exercises 43-46, x and y are related by the...Ch. 3 - Cost Analysis and Production A factorys weekly...Ch. 3 - Use of Books at a Library A town library estimates...Ch. 3 - Demand equation Suppose that the price p and...Ch. 3 - Volume of an Oil Spill An offshore oil well is...Ch. 3 - Weight and Surface Area Animal physiologists have...Ch. 3 - Sales and Advertising Suppose that a kitchen...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
SEE MORE TEXTBOOKS
Matrix Factorization - Numberphile; Author: Numberphile;https://www.youtube.com/watch?v=wTUSz-HSaBg;License: Standard YouTube License, CC-BY