
Concept explainers
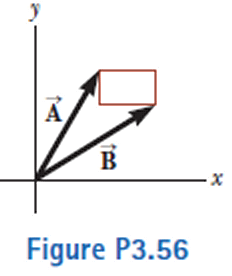
The rectangle shown in Figure P3.56 has sides parallel to the x and y axes. The position vectors of two corners are 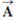 = 10.0 m at 50.0° and
= 10.0 m at 50.0° and 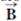 = 12.0 m at 30.0°. (a) Find the perimeter of the rectangle. (b) Find the magnitude and direction of the vector from the origin to the upper-right corner of the rectangle.
= 12.0 m at 30.0°. (a) Find the perimeter of the rectangle. (b) Find the magnitude and direction of the vector from the origin to the upper-right corner of the rectangle.
(a)
The perimeter of the rectangle.
Answer to Problem 3.56AP
The perimeter of the rectangle is
Explanation of Solution
Given info: The rectangle has sides parallel to the
The vector component of
Here,
Substitute
Thus, the vector component of
The vector component of
Here,
Substitute
Thus, the vector component of
The position vector
Here,
Substitute
Thus, the position vector for the vector
The component of vector
Here,
Substitute
Thus, the component of vector
The component of vector
Here,
Substitute
Thus, the component of vector
The position vector of the vector
Here,
Substitute
Thus, the position vector of the vector
The length of the rectangle is,
Here,
The width of the rectangle is,
Here,
The vector
Substitute
Formula to calculate the perimeter of the rectangle is,
Here,
Substitute
Conclusion:
Therefore, the perimeter of the rectangle is
(b)
The magnitude and direction of the vector from the origin to the upper right coordinate of the rectangle.
Answer to Problem 3.56AP
The magnitude and direction of the vector from the origin to the upper right coordinate of the rectangle is
Explanation of Solution
Given info: The rectangle has sides parallel to the
The vector of point
The vector
Here,
Substitute
Formula to calculate the magnitude of vector
Here,
Substitute
Formula to calculate the angle made by the vector
Here,
Substitute
Conclusion:
Therefore, the magnitude and direction of the vector from the origin to the upper right coordinate of the rectangle is
Want to see more full solutions like this?
Chapter 3 Solutions
Physics for Scientists and Engineers, Volume 1
Additional Science Textbook Solutions
Organic Chemistry
Microbiology Fundamentals: A Clinical Approach
Human Physiology: An Integrated Approach (8th Edition)
Fundamentals Of Thermodynamics
Anatomy & Physiology (6th Edition)
Principles of Anatomy and Physiology
- Physics different from a sea breeze from a land breezearrow_forwardFile Preview Design a capacitor for a special purpose. After graduating from medical school you and a friend take a three hour cruise to celebrate and end up stranded on an island. While looking for food, a spider falls on your friend giving them a heart attack. Recalling your physics, you realize you can build a make-shift defibrillator by constructing a capacitor from materials on the boat and charging it using the boat's battery. You know that the capacitor must hold 100 J of energy and be at 1000 V (fortunately this is an electric boat which has batteries that are 1000 V) to work. You decide to construct the capacitor by tightly sandwiching a single layer of Saran wrap between sheets of aluminum foil. You read the Saran wrap box and fortunately they tell you that it has a thickness 0.01 mm and dielectric constant of 2.3. The Saran wrap and foil are 40 cm wide and very long. How long is the final capacitor you build that saves your friend?arrow_forwardHow do I plot the force F in Matlba (of gravity pulling on the masses) versus spring displacement, and fit the data with a linear function to find the value for the spring constant. To get a linear fit, use polynomial order 1. Report the value of 'k' from the fit. What code is used?arrow_forward
- Ok im confused on this portion of the questions being asked. the first snip is the solution you gave which is correct. BUt now it is asking for this and im confused. The magnitude of the force F_11 is __________LB. The direction of the force F_11 is __________LB.arrow_forwardNo chatgpt pls will upvotearrow_forwardSolve and answer the problem correctly please. Thank you!!arrow_forward
- Solve and answer the problem correctly please. Thank you!!arrow_forwardSolve and answer the problem correctly and be sure to check your work. Thank you!!arrow_forwardThe spring in the figure has a spring constant of 1300 N/m. It is compressed 17.0 cm, then launches a 200 g block. The horizontal surface is frictionless, but the block’s coefficient of kinetic friction on the incline is 0.200. What distance d does the block sail through the air?arrow_forward
- Solve and answer the problem correctly and be sure to check your work. Thank you!!arrow_forwardSolve and answer the problem correctly and be sure to check your work. Thank you!!arrow_forwardA 10-m-long glider with a mass of 680 kg (including the passengers) is gliding horizontally through the air at 28 m/s when a 60 kg skydiver drops out by releasing his grip on the glider. What is the glider's speed just after the skydiver lets go?arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





