Concept explainers
Videos
a.
To explain: The area within 1 standard deviation of the
To compare: The area within 1 standard deviation of the mean by using applet and
a.
Answer to Problem 3.52E
The area within 1 standard deviation of the mean is 0.6826.
The area within 1 standard deviation of the mean by using applet and 68-95-99.7 rule is both approximately equal.
Explanation of Solution
Given info:
The mean and standard deviation of the
68-95-99.7 Rule:
About 68% of the observations fall within
About 95% of the observations fall within
About 99.7% of the observations fall within
Calculation:
Find the area of 1 standard deviation on either side of the mean using the normal density curve applet.
Applet procedure:
Step-by-step Applet procedure to find the area of 1 standard deviation on either side of the mean is given as follows:
- In Statistical Applets, choose Normal Density Curve.
- In the normal density curve drag one flag and place at 1 standard deviation on either side of the mean.
Output obtained from Applet:
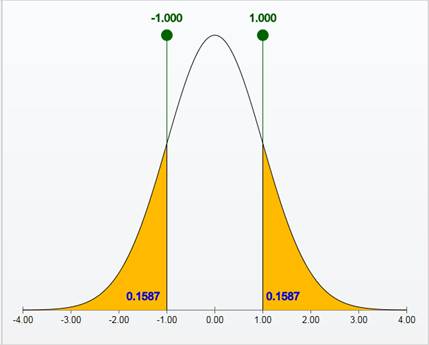
From the Applet output, the area of one standard deviation below −1 is 0.1587 and the above 1 is 0.1587.
The formula to find the area within 1 standard deviation of the mean is,
Thus, the area within 1 standard deviation of the mean is 0.6826. That is, about 68% of the observations fall within
From the 68-95-99.7 rule, the area within 1 standard deviation of the mean is about 68%.
Justification:
The result of the area within 1 standard deviation of the mean is approximately same by using the applet and the 68-95-99.7 rule.
b.
To explain: The area within 2 standard deviations of the mean and the area within 3 standard deviations of the mean.
To compare: The area within 2 standard deviations of the mean and the area within 3 standard deviations of the mean by using applet and 68-95-99.7 rule.
b.
Answer to Problem 3.52E
The area within 2 standard deviations of the mean is 0.9544 and the area within 3 standard deviations of the mean is 0.9974.
The area within 2 standard deviations of the mean by using applet and 68-95-99.7 rule is both approximately equal and the area within 3 standard deviations of the mean by using applet and 68-95-99.7 rule is both approximately equal.
Explanation of Solution
Calculation:
Finding the area of 2 standard deviations on either side of the mean:
Applet procedure:
Step-by-step Applet procedure to find the area of 2 standard deviations on either side of the mean is given as follows
- In Statistical Applets, choose Normal Density Curve.
- In the normal density curve drag one flag and place at 2 standard deviations on either side of the mean.
Output obtained from Applet:
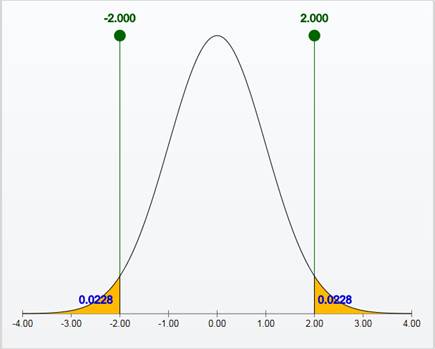
From the Applet output, the area to the left of −2 is 0.0228 and the area to right of 2 is 0.0228.
The formula to find the area within 2 standard deviations of the mean is,
Thus, the area within 2 standard deviations of the mean is 0.9544. That is, about 95% of the observations fall within
From the 68-95-99.7 rule, the area within 2 standard deviations of the mean is about 95%.
Finding the area of 3 standard deviations on either side of the mean:
Applet Procedure:
Step-by-step Applet procedure to find the area of 3 standard deviations on either side of the mean is given as follows
- In Statistical Applets, choose Normal Density Curve.
- In the normal density curve drag one flag and place at 3 standard deviations on either side of the mean.
Output obtained from Applet:
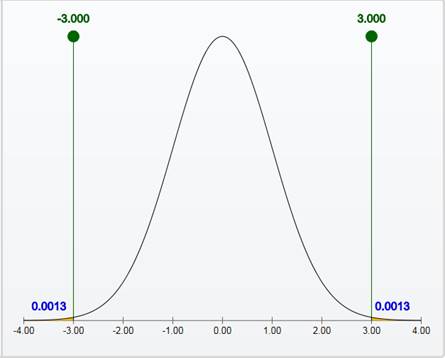
From the Applet output, the area to the left of −3 is 0.0013 and the area to right of 3 is 0.0013.
The formula to find the area within 3 standard deviations of the mean is,
Thus, the area within 3 standard deviations of the mean is 0.9974. That is, about 99.7% of the observations fall within
From the 68-95-99.7 rule, the area within 3 standard deviations of the mean is about 99.7%.
Justification:
The result of the area within 2 standard deviations of the mean is approximately same by using the applet and the 68-95-99.7 rule and also the result of the area within 3 standard deviations of the mean is approximately same by using the applet and the 68-95-99.7 rule.
Want to see more full solutions like this?
Chapter 3 Solutions
Loose-leaf Version for The Basic Practice of Statistics 7e & LaunchPad (Twelve Month Access)
- If a uniform distribution is defined over the interval from 6 to 10, then answer the followings: What is the mean of this uniform distribution? Show that the probability of any value between 6 and 10 is equal to 1.0 Find the probability of a value more than 7. Find the probability of a value between 7 and 9. The closing price of Schnur Sporting Goods Inc. common stock is uniformly distributed between $20 and $30 per share. What is the probability that the stock price will be: More than $27? Less than or equal to $24? The April rainfall in Flagstaff, Arizona, follows a uniform distribution between 0.5 and 3.00 inches. What is the mean amount of rainfall for the month? What is the probability of less than an inch of rain for the month? What is the probability of exactly 1.00 inch of rain? What is the probability of more than 1.50 inches of rain for the month? The best way to solve this problem is begin by a step by step creating a chart. Clearly mark the range, identifying the…arrow_forwardClient 1 Weight before diet (pounds) Weight after diet (pounds) 128 120 2 131 123 3 140 141 4 178 170 5 121 118 6 136 136 7 118 121 8 136 127arrow_forwardClient 1 Weight before diet (pounds) Weight after diet (pounds) 128 120 2 131 123 3 140 141 4 178 170 5 121 118 6 136 136 7 118 121 8 136 127 a) Determine the mean change in patient weight from before to after the diet (after – before). What is the 95% confidence interval of this mean difference?arrow_forward
- In order to find probability, you can use this formula in Microsoft Excel: The best way to understand and solve these problems is by first drawing a bell curve and marking key points such as x, the mean, and the areas of interest. Once marked on the bell curve, figure out what calculations are needed to find the area of interest. =NORM.DIST(x, Mean, Standard Dev., TRUE). When the question mentions “greater than” you may have to subtract your answer from 1. When the question mentions “between (two values)”, you need to do separate calculation for both values and then subtract their results to get the answer. 1. Compute the probability of a value between 44.0 and 55.0. (The question requires finding probability value between 44 and 55. Solve it in 3 steps. In the first step, use the above formula and x = 44, calculate probability value. In the second step repeat the first step with the only difference that x=55. In the third step, subtract the answer of the first part from the…arrow_forwardIf a uniform distribution is defined over the interval from 6 to 10, then answer the followings: What is the mean of this uniform distribution? Show that the probability of any value between 6 and 10 is equal to 1.0 Find the probability of a value more than 7. Find the probability of a value between 7 and 9. The closing price of Schnur Sporting Goods Inc. common stock is uniformly distributed between $20 and $30 per share. What is the probability that the stock price will be: More than $27? Less than or equal to $24? The April rainfall in Flagstaff, Arizona, follows a uniform distribution between 0.5 and 3.00 inches. What is the mean amount of rainfall for the month? What is the probability of less than an inch of rain for the month? What is the probability of exactly 1.00 inch of rain? What is the probability of more than 1.50 inches of rain for the month? The best way to solve this problem is begin by creating a chart. Clearly mark the range, identifying the lower and upper…arrow_forwardProblem 1: The mean hourly pay of an American Airlines flight attendant is normally distributed with a mean of 40 per hour and a standard deviation of 3.00 per hour. What is the probability that the hourly pay of a randomly selected flight attendant is: Between the mean and $45 per hour? More than $45 per hour? Less than $32 per hour? Problem 2: The mean of a normal probability distribution is 400 pounds. The standard deviation is 10 pounds. What is the area between 415 pounds and the mean of 400 pounds? What is the area between the mean and 395 pounds? What is the probability of randomly selecting a value less than 395 pounds? Problem 3: In New York State, the mean salary for high school teachers in 2022 was 81,410 with a standard deviation of 9,500. Only Alaska’s mean salary was higher. Assume New York’s state salaries follow a normal distribution. What percent of New York State high school teachers earn between 70,000 and 75,000? What percent of New York State high school…arrow_forward
- Pls help asaparrow_forwardSolve the following LP problem using the Extreme Point Theorem: Subject to: Maximize Z-6+4y 2+y≤8 2x + y ≤10 2,y20 Solve it using the graphical method. Guidelines for preparation for the teacher's questions: Understand the basics of Linear Programming (LP) 1. Know how to formulate an LP model. 2. Be able to identify decision variables, objective functions, and constraints. Be comfortable with graphical solutions 3. Know how to plot feasible regions and find extreme points. 4. Understand how constraints affect the solution space. Understand the Extreme Point Theorem 5. Know why solutions always occur at extreme points. 6. Be able to explain how optimization changes with different constraints. Think about real-world implications 7. Consider how removing or modifying constraints affects the solution. 8. Be prepared to explain why LP problems are used in business, economics, and operations research.arrow_forwardged the variance for group 1) Different groups of male stalk-eyed flies were raised on different diets: a high nutrient corn diet vs. a low nutrient cotton wool diet. Investigators wanted to see if diet quality influenced eye-stalk length. They obtained the following data: d Diet Sample Mean Eye-stalk Length Variance in Eye-stalk d size, n (mm) Length (mm²) Corn (group 1) 21 2.05 0.0558 Cotton (group 2) 24 1.54 0.0812 =205-1.54-05T a) Construct a 95% confidence interval for the difference in mean eye-stalk length between the two diets (e.g., use group 1 - group 2).arrow_forward
- An article in Business Week discussed the large spread between the federal funds rate and the average credit card rate. The table below is a frequency distribution of the credit card rate charged by the top 100 issuers. Credit Card Rates Credit Card Rate Frequency 18% -23% 19 17% -17.9% 16 16% -16.9% 31 15% -15.9% 26 14% -14.9% Copy Data 8 Step 1 of 2: Calculate the average credit card rate charged by the top 100 issuers based on the frequency distribution. Round your answer to two decimal places.arrow_forwardPlease could you check my answersarrow_forwardLet Y₁, Y2,, Yy be random variables from an Exponential distribution with unknown mean 0. Let Ô be the maximum likelihood estimates for 0. The probability density function of y; is given by P(Yi; 0) = 0, yi≥ 0. The maximum likelihood estimate is given as follows: Select one: = n Σ19 1 Σ19 n-1 Σ19: n² Σ1arrow_forward
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman