
Write the expression for computing the pressure in a fluid.
Expression of pressure in a fluid
Explanation of Solution
Given:-
Density of fluid and depth of fluid.
In a fluid, if the fluid is stationary, the state of pressure at a point may be defined using pascal's law and hydrostatic law.
According to pascal's law, In a fluid, at a particular point, pressure acts uniformly and is equal in all the directions.
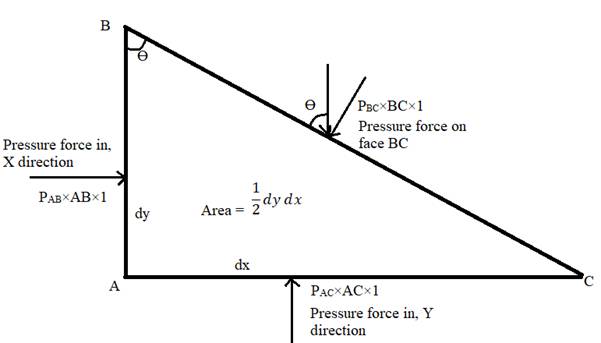
Resolving the forces in x direction,
Resolving the pressure forces in the y direction
Since the choice of fluid element is arbitrary, force on BC could be in any direction, Hence pressure at a point in all the direction is uniform and is equal in all direction.
The hydrostatic law states that the rate of increase with respect to depth in a stationary fluid is equal to the specific weight of the fluid.
To prove this, consider a small rectangular shaped fluid element of cross sectional area
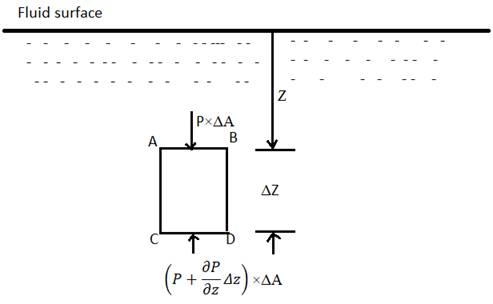
further at a given depth in a fluid, for a given density,
specific weight, w=
Hence to find the value of pressure at any depth Z, integrate both sides of eq2
Conclusion:
Pressure, P=
Want to see more full solutions like this?
Chapter 3 Solutions
Applied Fluid Mechanics
Additional Engineering Textbook Solutions
Electric Circuits. (11th Edition)
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Database Concepts (8th Edition)
Concepts Of Programming Languages
Degarmo's Materials And Processes In Manufacturing
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
- The tooth numbers for the gear train illustrated are N₂ = 24, N3 = 18, №4 = 30, №6 = 36, and N₁ = 54. Gear 7 is fixed. If shaft b is turned through 5 revolutions, how many turns will shaft a make? a 5 [6] barrow_forwardCE-112 please solve this problem step by step and give me the correct answerarrow_forwardCE-112 please solve this problem step by step and give me the correct answerarrow_forward
- CE-112 solve this problem step by step and give me the correct answer pleasearrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forwardPlease do not use any AI tools to solve this question. I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor. No AI-generated responses, please.arrow_forward
 Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning
Refrigeration and Air Conditioning Technology (Mi...Mechanical EngineeringISBN:9781305578296Author:John Tomczyk, Eugene Silberstein, Bill Whitman, Bill JohnsonPublisher:Cengage Learning Automotive Technology: A Systems Approach (MindTa...Mechanical EngineeringISBN:9781133612315Author:Jack Erjavec, Rob ThompsonPublisher:Cengage Learning
Automotive Technology: A Systems Approach (MindTa...Mechanical EngineeringISBN:9781133612315Author:Jack Erjavec, Rob ThompsonPublisher:Cengage Learning International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L Electrical Transformers and Rotating MachinesMechanical EngineeringISBN:9781305494817Author:Stephen L. HermanPublisher:Cengage Learning
Electrical Transformers and Rotating MachinesMechanical EngineeringISBN:9781305494817Author:Stephen L. HermanPublisher:Cengage Learning Precision Machining Technology (MindTap Course Li...Mechanical EngineeringISBN:9781285444543Author:Peter J. Hoffman, Eric S. Hopewell, Brian JanesPublisher:Cengage Learning
Precision Machining Technology (MindTap Course Li...Mechanical EngineeringISBN:9781285444543Author:Peter J. Hoffman, Eric S. Hopewell, Brian JanesPublisher:Cengage Learning Understanding Motor ControlsMechanical EngineeringISBN:9781337798686Author:Stephen L. HermanPublisher:Delmar Cengage Learning
Understanding Motor ControlsMechanical EngineeringISBN:9781337798686Author:Stephen L. HermanPublisher:Delmar Cengage Learning





