Chapter 3, Problem 28E

Compute the power absorbed by each element in the circuit of Fig. 3.68 if the mysterious element X is (a) a 13 Ω resistor; (b) a dependent voltage source labeled 4v₁, “+” reference on top; (c) a dependent voltage source labeled 4i_x, “+” reference on top.

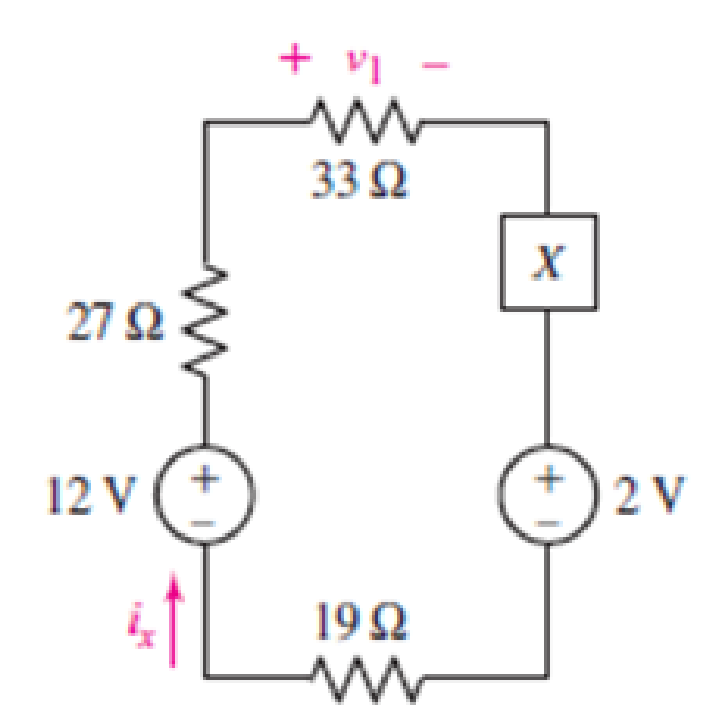
FIGURE 3.68

To determine

Find the power absorbed by each element.

Answer to Problem 28E

Power absorbed by $12\text{ V}$ independent voltage source is $-1.304\text{W}$, power absorbed by $27\Omega$ resistor is $\text{319}\text{mW}$, power absorbed by $33\Omega$ resistor is $\text{390}\text{mW}$, power absorbed by mysterious element $X$ is $153.6\text{mW}$, power absorbed by $2\text{ V}$ independent voltage source is $217.4\text{mW}$ and power absorbed by $19\Omega$ resistor is $224.6\text{mW}$.

Explanation of Solution

Given Data:

Element $X$ is a $13\text{ Ω}$ resistor.

Formula used:

The expression for power absorbed by voltage source is as follows.

$p=vi$ (1)

Here,

$p$ is the power absorbed by voltage source,

$i$ is the current and

$v$ is the voltage.

The expression for power absorbed by resistor is as follows.

$p=i^{2}R$ (2)

Here,

$p$ is the power absorbed,

$i$ is the current and

$R$ is value of resistance.

Calculation:

The circuit diagram is redrawn as shown in Figure 1.

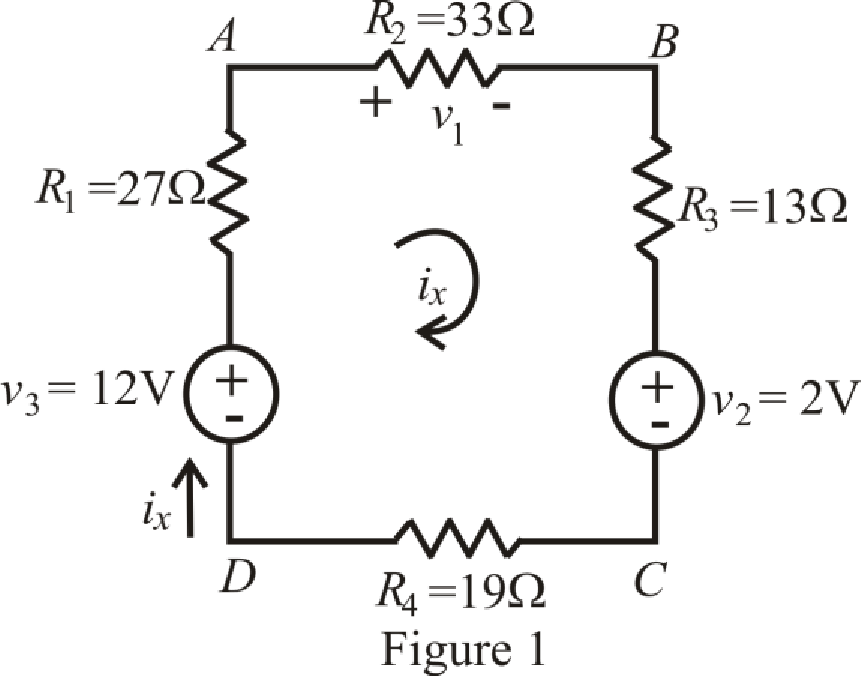
Refer to the redrawn Figure 1.

The expression for KVL in mesh $DABCD$ is as follows.

$-v_3+i_x{R}_1+i_x{R}_2+i_x{R}_3+v_2+i_x{R}_4=0$ (3)

Here,

$i_x$ is the current in the circuit,

$v_2$ and $v_3$ are the voltages in the circuit and

$R_1$, $R_2$, $R_3$ and $R_4$ are the resistances in the circuit.

Substitute $12\text{V}$ for $v_3$, $2\text{V}$ for $v_2$, $27\text{Ω}$ for $R_1$, $33\text{Ω}$ for $R_2$, $13\text{Ω}$ for $R_3$ and $19\text{Ω}$ for $R_4$ in equation (3).

$-12\text{V}+i_x\left(27\text{Ω}\right)+i_x\left(33\text{Ω}\right)+i_x\left(13\text{Ω}\right)+2\text{V}+i_x\left(19\text{Ω}\right)=0$

$-10\text{V}+i_x\left(92\text{Ω}\right)=0$ (4)

Rearrange equation (4) for $i_x$.

$\begin{array}{c}{i}_x=\frac{10\text{V}}{92\text{Ω}}\\ =0.1087\text{A}\end{array}$

Current is leaving the positive terminal and we are calculating power absorbed hence current should leave by negative terminal so we will use magnitude of voltage with negative sign, therefore, value of $v_1$ is $-12\text{V}$.

Substitute $-12\text{V}$ for $v$ and $0.1087\text{A}$ for $i$ in equation (1).

$\begin{array}{c}p=\left(-12\text{V}\right)\left(0.1087\text{A}\right)\\ =-1.304\text{W}\end{array}$

So power absorbed by independent voltage source $v_3$ is $-1.304\text{W}$.

Substitute $27\text{Ω}$ for $R$ and $0.1087\text{A}$ for $i$ in equation (2).

$\begin{array}{c}p={\left(0.1087\text{A}\right)}^2\left(27\text{Ω}\right)\\ =\left(0.01182{\text{A}}^2\right)\left(27\text{Ω}\right)\\ =0.3190\text{W}\\ =\text{319}\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So, the power absorbed by resistor $R_1$ is $\text{319}\text{mW}$.

Substitute $33\text{Ω}$ for $R$ and $0.1087\text{A}$ for $i$ in equation (2).

$\begin{array}{c}p={\left(0.1087\text{A}\right)}^2\left(33\text{Ω}\right)\\ =\left(0.01182{\text{A}}^2\right)\left(33\text{Ω}\right)\\ =0.39006\text{W}\\ =\text{390}\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by resistor $R_2$ is $\text{390}\text{mW}$.

Substitute $13\text{Ω}$ for $R$ and $0.1087\text{A}$ for $i$ in equation (3),

$\begin{array}{c}p={\left(0.1087\text{A}\right)}^2\left(13\text{Ω}\right)\\ =\left(0.01182{\text{A}}^2\right)\left(13\text{Ω}\right)\\ =0.1536\text{W}\\ =153.6\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by resistor $R_3$ is $153.6\text{mW}$.

Substitute $2\text{V}$ for $v$ and $0.1087\text{A}$ for $i$ in equation (1),

$\begin{array}{c}p=\left(2\text{V}\right)\left(0.1087\text{A}\right)\\ =0.2174\text{W}\\ =217.4\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by independent voltage source $v_2$ is $217.4\text{mW}$.

Substitute $19\text{Ω}$ for $R$ and $0.1087\text{A}$ for $i$ in equation (3).

$\begin{array}{c}p={\left(0.1087\text{A}\right)}^2\left(19\text{Ω}\right)\\ =\left(0.01182{\text{A}}^2\right)\left(19\text{Ω}\right)\\ =0.2246\text{W}\\ =224.6\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by resistor $R_4$ is $224.6\text{mW}$.

Conclusion:

Thus, power absorbed by $12\text{ V}$ independent voltage source is $-1.304\text{W}$, power absorbed by $27\Omega$ resistor is $\text{319}\text{mW}$, power absorbed by $33\Omega$ resistor is $\text{390}\text{mW}$, power absorbed by mysterious element $X$ is $153.6\text{mW}$, power absorbed by $2\text{ V}$ independent voltage source is $217.4\text{mW}$ and power absorbed by $19\Omega$ resistor is $224.6\text{mW}$.

To determine

Find power absorbed by each element.

Answer to Problem 28E

Power absorbed by $12\text{ V}$ independent voltage source is $-568.8\text{mW}$, power absorbed by $27\Omega$ resistor is $\text{60}\text{.7}\text{mW}$, power absorbed by $33\Omega$ resistor is $\text{74}\text{.2}\text{mW}$, power absorbed by mysterious element $X$ is $296.6\text{mW}$, power absorbed by $2\text{ V}$ independent voltage source is $94.8\text{mW}$ and power absorbed by $19\Omega$ resistor is $\text{42}\text{.7}\text{mW}$.

Explanation of Solution

Given Data:

Element $X$ is a dependent voltage source labeled $4v_1$ positive reference on top.

Calculation:

The circuit diagram is redrawn as shown in Figure 2,

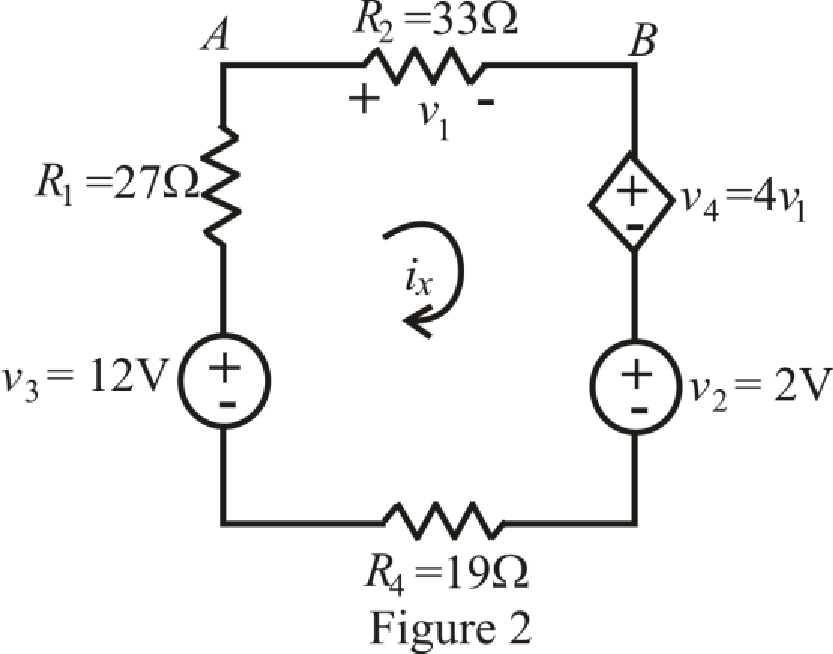
Refer to the redrawn Figure 2,

The expression for KVL in mesh $DABCD$ is as follows,

$-v_3+i_x{R}_1+i_x{R}_2+4v_1+v_2+i_x{R}_4=0$ (5)

Here,

$i_x$ is the current in the circuit,

$v_1$, $v_2$ and $v_3$ are the voltages in the circuit and

$R_1$, $R_2$ and $R_4$ are the resistances in the circuit.

The expression for voltage $v_1$ is as follows,

$v_1=i_x{R}_2$ (6)

Here,

$v_1$ is the voltage,

$i_x$ is the current and

$R_2$ is value of resistance.

The expression for voltage $v_4$ is as follows,

$v_4=4v_1$ (7)

Here,

$v_1$ and $v_4$ are the voltages.

Refer to the redrawn Figure 2,

Substitute $33\text{Ω}$ for $R_2$ in equation (6),

$v_1=i_x\left(33\text{Ω}\right)$ (8)

Substitute $12\text{V}$ for $v_3$, $2\text{V}$ for $v_2$, $27\text{Ω}$ for $R_1$, $33\text{Ω}$ for $R_2$, $i_x\left(33\text{Ω}\right)$ for $v_1$ and $19\text{Ω}$ for $R_4$ in equation (5),

$-12\text{V}+i_x\left(27\text{Ω}\right)+i_x\left(33\text{Ω}\right)+4\left(i_x\left(33\text{Ω}\right)\right)+2\text{V}+i_x\left(19\text{Ω}\right)=0$

$-10\text{V}+i_x\left(211\text{Ω}\right)=0$ (9)

Rearrange equation (9) for $i_x$,

$\begin{array}{c}{i}_x=\frac{10\text{V}}{211\text{Ω}}\\ =0.0474\text{A}\end{array}$

Current is leaving the positive terminal and we are calculating power absorbed hence current should leave by negative terminal so we will use magnitude of voltage with negative sign, therefore, value of $v_1$ is $-12\text{V}$.

Substitute $-12\text{V}$ for $v$ and $0.0474\text{A}$ for $i$ in equation (1),

$\begin{array}{c}p=\left(-12\text{V}\right)\left(0.0474\text{A}\right)\\ =-0.5688\text{W}\\ =-568.8\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by independent voltage source $v_3$ is $-568.8\text{mW}$.

Substitute $27\text{Ω}$ for $R$ and $0.0474\text{A}$ for $i$ in equation (2),

$\begin{array}{c}p={\left(0.0474\text{A}\right)}^2\left(27\text{Ω}\right)\\ =\left(0.002247{\text{A}}^2\right)\left(27\text{Ω}\right)\\ =0.0607\text{W}\\ =\text{60}\text{.7}\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by resistor $R_1$ is $\text{60}\text{.7}\text{mW}$.

Substitute $33\text{Ω}$ for $R$ and $0.0474\text{A}$ for $i$ in equation (2),

$\begin{array}{c}p={\left(0.0474\text{A}\right)}^2\left(33\text{Ω}\right)\\ =\left(0.002247{\text{A}}^2\right)\left(33\text{Ω}\right)\\ =0.0742\text{W}\\ =\text{74}\text{.2}\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by resistor $R_2$ is $\text{74}\text{.2}\text{mW}$.

Substitute $0.0474\text{A}$ for $i_x$ in equation (8),

$\begin{array}{c}{v}_1=\left(0.0474\text{A}\right)\left(33\text{Ω}\right)\\ =1.564\text{V}\end{array}$

Substitute $1.564\text{V}$ for $v_1$ in equation (7),

$\begin{array}{c}{v}_2=4\left(1.564\text{V}\right)\\ =6.257\text{V}\end{array}$

Substitute $6.257\text{V}$ for $v$ and $0.0474\text{A}$ for $i$ in equation (1),

$\begin{array}{c}p=\left(6.257\text{V}\right)\left(0.0474\text{A}\right)\\ =0.2966\text{W}\\ =296.6\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by dependent voltage source $v_4$ is $296.6\text{mW}$.

Substitute $2\text{V}$ for $v$ and $0.0474\text{A}$ for $i$ in equation (1),

$\begin{array}{c}p=\left(2\text{V}\right)\left(0.0474\text{A}\right)\\ =0.0948\text{W}\\ =94.8\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by independent voltage source $v_2$ is $94.8\text{mW}$.

Substitute $19\text{Ω}$ for $R$ and $0.0474\text{A}$ for $i$ in equation (2),

$\begin{array}{c}p={\left(0.0474\text{A}\right)}^2\left(19\text{Ω}\right)\\ =\left(0.002247{\text{A}}^2\right)\left(19\text{Ω}\right)\\ =0.0427\text{W}\\ =\text{42}\text{.7}\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by resistor $R_4$ is $\text{42}\text{.7}\text{mW}$.

Conclusion:

Thus, power absorbed by $12\text{ V}$ independent voltage source is $-568.8\text{mW}$, power absorbed by $27\Omega$ resistor is $\text{60}\text{.7}\text{mW}$, power absorbed by $33\Omega$ resistor is $\text{74}\text{.2}\text{mW}$, power absorbed by mysterious element $X$ is $296.6\text{mW}$, power absorbed by $2\text{ V}$ independent voltage source is $94.8\text{mW}$ and power absorbed by $19\Omega$ resistor is $\text{42}\text{.7}\text{mW}$.

To determine

Find power absorbed by each element.

Answer to Problem 28E

Power absorbed by $12\text{ V}$ independent voltage source is $-1.446\text{W}$, power absorbed by $27\Omega$ resistor is $391.5\text{mW}$, power absorbed by $33\Omega$ resistor is $478.5\text{mW}$, power absorbed by mysterious element $X$ is $58.1\text{mW}$, power absorbed by $2\text{ V}$ independent voltage source is $241\text{mW}$ and power absorbed by $19\Omega$ resistor is $275.5\text{mW}$.

Explanation of Solution

Given Data:

Element $X$ is a dependent voltage source labeled $4i_x$ positive reference on top.

Calculation:

The circuit diagram is redrawn as shown in Figure 3.

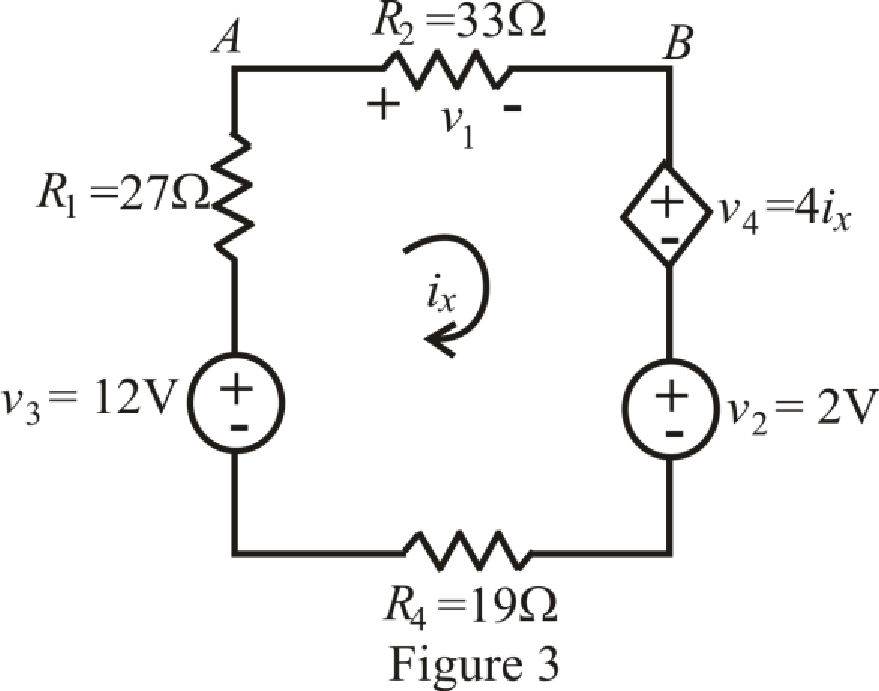
Refer to the redrawn Figure 3,

The expression for KVL in mesh $DABCD$ is as follows,

$-v_3+i_x{R}_1+i_x{R}_2+4i_x+v_2+i_x{R}_4=0$ (10)

Here,

$i_x$ is the current in the circuit,

$v_2$ and $v_3$ are the voltages in the circuit and

$R_1$, $R_2$ and $R_4$ are the resistances in the circuit.

The expression for voltage $v_4$ is as follows,

$v_4=4i_x$ (11)

Here,

$v_4$ is the voltages and

$i_x$ is the current in the circuit.

Refer to the redrawn Figure 2,

Substitute $12\text{V}$ for $v_3$, $2\text{V}$ for $v_2$, $27\text{Ω}$ for $R_1$, $33\text{Ω}$ for $R_2$, and $19\text{Ω}$ for $R_4$ in equation (5),

$-12\text{V}+i_x\left(27\text{Ω}\right)+i_x\left(33\text{Ω}\right)+4i_x+2\text{V}+i_x\left(19\text{Ω}\right)=0$

$-10\text{V}+i_x\left(83\text{Ω}\right)=0$ (12)

Rearrange equation (12) for $i_x$,

$\begin{array}{c}{i}_x=\frac{10\text{V}}{83\text{Ω}}\\ =0.1205\text{A}\end{array}$

Current is leaving the positive terminal and we are calculating power absorbed hence current should leave by negative terminal so we will use magnitude of voltage with negative sign, therefore, value of $v_1$ is $-12\text{V}$.

Substitute $-12\text{V}$ for $v$ and $0.1205\text{A}$ for $i$ in equation (1),

$\begin{array}{c}p=\left(-12\text{V}\right)\left(0.1205\text{A}\right)\\ =-1.446\text{W}\end{array}$

So power absorbed by independent voltage source $v_3$ is $-1.446\text{W}$.

Substitute $27\text{Ω}$ for $R$ and $0.1205\text{A}$ for $i$ in equation (2),

$\begin{array}{c}p={\left(0.1205\text{A}\right)}^2\left(27\text{Ω}\right)\\ =\left(0.0145{\text{A}}^2\right)\left(27\text{Ω}\right)\\ =0.3915\text{W}\\ =391.5\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by resistor $R_1$ is $391.5\text{mW}$.

Substitute $33\text{Ω}$ for $R$ and $0.1205\text{A}$ for $i$ in equation (2),

$\begin{array}{c}p={\left(0.1205\text{A}\right)}^2\left(33\text{Ω}\right)\\ =\left(0.0145{\text{A}}^2\right)\left(33\text{Ω}\right)\\ =0.4785\text{W}\\ =478.5\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by resistor $R_2$ is $478.5\text{mW}$.

Substitute $0.1205\text{A}$ for $i_x$ in equation (11),

$\begin{array}{c}{v}_4=4\left(0.1205\text{A}\right)\\ =0.482\text{V}\end{array}$

Substitute $0.482\text{V}$ for $v$ and $0.1205\text{A}$ for $i$ in equation (1),

$\begin{array}{c}p=\left(0.482\text{V}\right)\left(0.1205\text{A}\right)\\ =0.0581\text{W}\\ =58.1\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by dependent voltage source $v_4$ is $58.1\text{mW}$.

Substitute $2\text{V}$ for $v$ and $0.1205\text{A}$ for $i$ in equation (1),

$\begin{array}{c}p=\left(2\text{V}\right)\left(0.1205\text{A}\right)\\ =0.241\text{W}\\ =241\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by independent voltage source $v_2$ is $241\text{mW}$.

Substitute $19\text{Ω}$ for $R$ and $0.1205\text{A}$ for $i$ in equation (2),

$\begin{array}{c}p={\left(0.1205\text{A}\right)}^2\left(19\text{Ω}\right)\\ =\left(0.0145{\text{A}}^2\right)\left(19\text{Ω}\right)\\ =0.2755\text{W}\\ =275.5\text{mW}\left\{\because 1\text{W}={10}^3\text{mW}\right\}\end{array}$

So power absorbed by resistor $R_4$ is $275.5\text{mW}$.

Conclusion:

Thus, power absorbed by $12\text{ V}$ independent voltage source is $-1.446\text{W}$, power absorbed by $27\Omega$ resistor is $391.5\text{mW}$, power absorbed by $33\Omega$ resistor is $478.5\text{mW}$, power absorbed by mysterious element $X$ is $58.1\text{mW}$, power absorbed by $2\text{ V}$ independent voltage source is $241\text{mW}$ and power absorbed by $19\Omega$ resistor is $275.5\text{mW}$.