
Operations Research: Applications and Algorithms
4th Edition
ISBN: 9780357907818
Author: WINSTON
Publisher: Cengage Learning US
expand_more
expand_more
format_list_bulleted
Question
Chapter 3, Problem 1RP
Program Plan Intro
Linear
- The linear programming(LP) is also known as linear optimization.
- Consider a mathematical model, and its requirements are used to represent by the linear relationships. The linear programming is the best method to achieve the best outcome of this mathematical model. The outcomes may be, maximum profit or lower cost.
- The linear optimization is also called as mathematical optimization because, it is a special case of mathematical programming.
- More formally, the LP is a technique for optimizing linear objective function subject to constraints of linear equality and linear inequality.
Expert Solution & Answer
Explanation of Solution
Linear programming for solving the problem:
Let
Then,
Explanation:
- The above programming statements are used to solve the beer and ale problem. In this there are two variables “x” and “y” used to represent the barrels of beer produced and barrels of ale produced respectively.
- The above statements give the formula to maximize the profit. Which is “5x + 2y”.
Solving LP graphically:
| Beer | Ale | Total | |
| Corn | 5lb | 2lb | 60 |
| Hopes | 2lb | 1lb | 25 |
Let
LP graph:
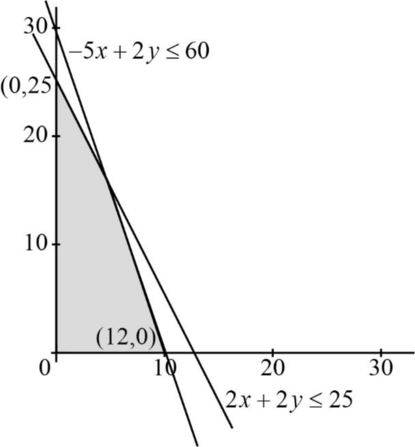
Vertices are,
Profit function:
The profit function at
The profit function at
The profit function at
The profit is maximized at the points,
That is 10 barrels of beer and 5 barrels of ale.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
I help understanding this question
d'y + 4dy +3y = a, Initial Conditions: y(0) = 5 & y'(0)=0
Where a = 10
a) Find y(t) =yh(t) +yp(t) in time domainIs the system over-damped, under-damped, or critical?
b) Find y(t) using Laplace Transforms
Given f(t)=a sin(ßt)
a = 10 & ß = 23
Find the Laplace Transform using the definition F(s) = ∫f(t)e-stdt
Please do not use any AI tools to solve this question.
I need a fully manual, step-by-step solution with clear explanations, as if it were done by a human tutor.
No AI-generated responses, please.
Chapter 3 Solutions
Operations Research: Applications and Algorithms
Ch. 3.1 - Prob. 1PCh. 3.1 - Prob. 2PCh. 3.1 - Prob. 3PCh. 3.1 - Prob. 4PCh. 3.1 - Prob. 5PCh. 3.2 - Prob. 1PCh. 3.2 - Prob. 2PCh. 3.2 - Prob. 3PCh. 3.2 - Prob. 4PCh. 3.2 - Prob. 5P
Ch. 3.2 - Prob. 6PCh. 3.3 - Prob. 1PCh. 3.3 - Prob. 2PCh. 3.3 - Prob. 3PCh. 3.3 - Prob. 4PCh. 3.3 - Prob. 5PCh. 3.3 - Prob. 6PCh. 3.3 - Prob. 7PCh. 3.3 - Prob. 8PCh. 3.3 - Prob. 9PCh. 3.3 - Prob. 10PCh. 3.4 - Prob. 1PCh. 3.4 - Prob. 2PCh. 3.4 - Prob. 3PCh. 3.4 - Prob. 4PCh. 3.5 - Prob. 1PCh. 3.5 - Prob. 2PCh. 3.5 - Prob. 3PCh. 3.5 - Prob. 4PCh. 3.5 - Prob. 5PCh. 3.5 - Prob. 6PCh. 3.5 - Prob. 7PCh. 3.6 - Prob. 1PCh. 3.6 - Prob. 2PCh. 3.6 - Prob. 3PCh. 3.6 - Prob. 4PCh. 3.6 - Prob. 5PCh. 3.7 - Prob. 1PCh. 3.8 - Prob. 1PCh. 3.8 - Prob. 2PCh. 3.8 - Prob. 3PCh. 3.8 - Prob. 4PCh. 3.8 - Prob. 5PCh. 3.8 - Prob. 6PCh. 3.8 - Prob. 7PCh. 3.8 - Prob. 8PCh. 3.8 - Prob. 9PCh. 3.8 - Prob. 10PCh. 3.8 - Prob. 11PCh. 3.8 - Prob. 12PCh. 3.8 - Prob. 13PCh. 3.8 - Prob. 14PCh. 3.9 - Prob. 1PCh. 3.9 - Prob. 2PCh. 3.9 - Prob. 3PCh. 3.9 - Prob. 4PCh. 3.9 - Prob. 5PCh. 3.9 - Prob. 6PCh. 3.9 - Prob. 7PCh. 3.9 - Prob. 8PCh. 3.9 - Prob. 9PCh. 3.9 - Prob. 10PCh. 3.9 - Prob. 11PCh. 3.9 - Prob. 12PCh. 3.9 - Prob. 13PCh. 3.9 - Prob. 14PCh. 3.10 - Prob. 1PCh. 3.10 - Prob. 2PCh. 3.10 - Prob. 3PCh. 3.10 - Prob. 4PCh. 3.10 - Prob. 5PCh. 3.10 - Prob. 6PCh. 3.10 - Prob. 7PCh. 3.10 - Prob. 8PCh. 3.10 - Prob. 9PCh. 3.11 - Prob. 1PCh. 3.11 - Show that Finco’s objective function may also be...Ch. 3.11 - Prob. 3PCh. 3.11 - Prob. 4PCh. 3.11 - Prob. 7PCh. 3.11 - Prob. 8PCh. 3.11 - Prob. 9PCh. 3.12 - Prob. 2PCh. 3.12 - Prob. 3PCh. 3.12 - Prob. 4PCh. 3 - Prob. 1RPCh. 3 - Prob. 2RPCh. 3 - Prob. 3RPCh. 3 - Prob. 4RPCh. 3 - Prob. 5RPCh. 3 - Prob. 6RPCh. 3 - Prob. 7RPCh. 3 - Prob. 8RPCh. 3 - Prob. 9RPCh. 3 - Prob. 10RPCh. 3 - Prob. 11RPCh. 3 - Prob. 12RPCh. 3 - Prob. 13RPCh. 3 - Prob. 14RPCh. 3 - Prob. 15RPCh. 3 - Prob. 16RPCh. 3 - Prob. 17RPCh. 3 - Prob. 18RPCh. 3 - Prob. 19RPCh. 3 - Prob. 20RPCh. 3 - Prob. 21RPCh. 3 - Prob. 22RPCh. 3 - Prob. 23RPCh. 3 - Prob. 24RPCh. 3 - Prob. 25RPCh. 3 - Prob. 26RPCh. 3 - Prob. 27RPCh. 3 - Prob. 28RPCh. 3 - Prob. 29RPCh. 3 - Prob. 30RPCh. 3 - Graphically find all solutions to the following...Ch. 3 - Prob. 32RPCh. 3 - Prob. 33RPCh. 3 - Prob. 34RPCh. 3 - Prob. 35RPCh. 3 - Prob. 36RPCh. 3 - Prob. 37RPCh. 3 - Prob. 38RPCh. 3 - Prob. 39RPCh. 3 - Prob. 40RPCh. 3 - Prob. 41RPCh. 3 - Prob. 42RPCh. 3 - Prob. 43RPCh. 3 - Prob. 44RPCh. 3 - Prob. 45RPCh. 3 - Prob. 46RPCh. 3 - Prob. 47RPCh. 3 - Prob. 48RPCh. 3 - Prob. 49RPCh. 3 - Prob. 50RPCh. 3 - Prob. 51RPCh. 3 - Prob. 52RPCh. 3 - Prob. 53RPCh. 3 - Prob. 54RPCh. 3 - Prob. 56RPCh. 3 - Prob. 57RPCh. 3 - Prob. 58RPCh. 3 - Prob. 59RPCh. 3 - Prob. 60RPCh. 3 - Prob. 61RPCh. 3 - Prob. 62RPCh. 3 - Prob. 63RP
Knowledge Booster
Similar questions
- Obtain the MUX design for the function F(X,Y,Z) = (0,3,4,7) using an off-the-shelf MUX with an active low strobe input (E).arrow_forwardI cannot program smart home automation rules from my device using a computer or phone, and I would like to know how to properly connect devices such as switches and sensors together ? Cisco Packet Tracer 1. Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forwardusing r language for integration theta = integral 0 to infinity (x^4)*e^(-x^2)/2 dx (1) use the density function of standard normal distribution N(0,1) f(x) = 1/sqrt(2pi) * e^(-x^2)/2 -infinity <x<infinity as importance function and obtain an estimate theta 1 for theta set m=100 for the estimate whatt is the estimate theta 1? (2)use the density function of gamma (r=5 λ=1/2)distribution f(x)=λ^r/Γ(r) x^(r-1)e^(-λx) x>=0 as importance function and obtain an estimate theta 2 for theta set m=1000 fir the estimate what is the estimate theta2? (3) use simulation (repeat 1000 times) to estimate the variance of the estimates theta1 and theta 2 which one has smaller variance?arrow_forward
- using r language A continuous random variable X has density function f(x)=1/56(3x^2+4x^3+5x^4).0<=x<=2 (1) secify the density g of the random variable Y you find for the acceptance rejection method. (2) what is the value of c you choose to use for the acceptance rejection method (3) use the acceptance rejection method to generate a random sample of size 1000 from the distribution of X .graph the density histogram of the sample and compare it with the density function f(x)arrow_forwardusing r language a continuous random variable X has density function f(x)=1/4x^3e^-(pi/2)^4,x>=0 derive the probability inverse transformation F^(-1)x where F(x) is the cdf of the random variable Xarrow_forwardusing r language in an accelerated failure test, components are operated under extreme conditions so that a substantial number will fail in a rather short time. in such a test involving two types of microships 600 chips manufactured by an existing process were tested and 125 of them failed then 800 chips manufactured by a new process were tested and 130 of them failed what is the 90%confidence interval for the difference between the proportions of failure for chips manufactured by two processes? using r languagearrow_forward
- I want a picture of the tools and the pictures used Cisco Packet Tracer Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forwardA. What will be printed executing the code above?B. What is the simplest way to set a variable of the class Full_Date to January 26 2020?C. Are there any empty constructors in this class Full_Date?a. If there is(are) in which code line(s)?b. If there is not, how would an empty constructor be? (create the code lines for it)D. Can the command std::cout << d1.m << std::endl; be included after line 28 withoutcausing an error?a. If it can, what will be printed?b. If it cannot, how could this command be fixed?arrow_forwardCisco Packet Tracer Smart Home Automation:o Connect a temperature sensor and a fan to a home gateway.o Configure the home gateway so that the fan is activated when the temperature exceedsa set threshold (e.g., 30°C).2. WiFi Network Configuration:o Set up a wireless LAN with a unique SSID.o Enable WPA2 encryption to secure the WiFi network.o Implement MAC address filtering to allow only specific clients to connect.3. WLC Configuration:o Deploy at least two wireless access points connected to a Wireless LAN Controller(WLC).o Configure the WLC to manage the APs, broadcast the configured SSID, and applyconsistent security settings across all APs.arrow_forward
- Transform the TM below that accepts words over the alphabet Σ= {a, b} with an even number of a's and b's in order that the output tape head is positioned over the first letter of the input, if the word is accepted, and all letters a should be replaced by the letter x. For example, for the input aabbaa the tape and head at the end should be: [x]xbbxx z/z,R b/b,R F ① a/a,R b/b,R a/a, R a/a,R b/b.R K a/a,R L b/b,Rarrow_forwardGiven the C++ code below, create a TM that performs the same operation, i.e., given an input over the alphabet Σ= {a, b} it prints the number of letters b in binary. 1 #include 2 #include 3 4- int main() { std::cout > str; for (char c : str) { if (c == 'b') count++; 5 std::string str; 6 int count = 0; 7 char buffer [1000]; 8 9 10 11- 12 13 14 } 15 16- 17 18 19 } 20 21 22} std::string binary while (count > 0) { binary = std::to_string(count % 2) + binary; count /= 2; std::cout << binary << std::endl; return 0;arrow_forwardConsidering the CFG described below, answer the following questions. Σ = {a, b} • NT = {S} Productions: P1 S⇒aSa P2 P3 SbSb S⇒ a P4 S⇒ b A. List one sequence of productions that can accept the word abaaaba; B. Give three 5-letter words that can be accepted by this CFG; C. Create a Pushdown automaton capable of accepting the language accepted by this CFG.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole

Operations Research : Applications and Algorithms
Computer Science
ISBN:9780534380588
Author:Wayne L. Winston
Publisher:Brooks Cole